P8865 NOIP2022 种花 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)。
记 \(a(x, y)\) 代表原文的 \(a_{x, y}\)。
考虑对每个点统计:左上角在该点的 \(\texttt{C-}\),\(\texttt{F-}\) 的数量。最终答案累加每个点对应的答案即可。
那么接下来我们想:对于一个点怎么计算对应的答案?我们生成一个地图来看看:

其中白色代表可以放置花,红色代表不可放置。现在,我们要计算左上角在 \((1, 1)\) 的 \(\texttt{C-}\) 的数量。
较容易看出,\(\texttt{C-}\) 的最上面那一横总共有 \(3\) 种画法,下面是其中一种:
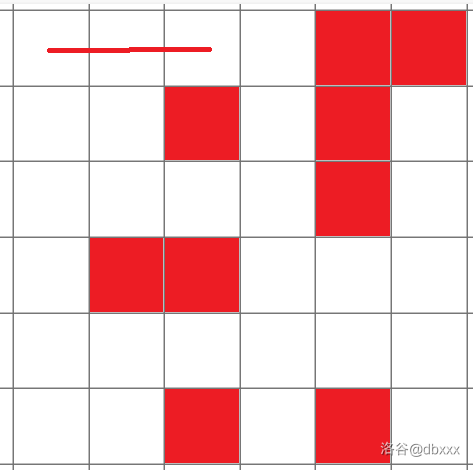
考虑 \(3\) 的意义,其实它是从 \((1, 1)\) 开始,往右最多有几个连续的白色方块(不统计 \((1, 1)\) 本身)。
据此,我们考虑预处理 \(r(x, y)\) 表示 \((x, y)\) 开始向右最多有几个连续的 \(0\)(不统计 \((x, y)\) 本身)。特别地,当 \(a(x, y) = 1\) 时,记 \(r(x, y) = -1\)。
\(r\) 可以通过 \(\Theta(nm)\) 的递推(或者说后缀和)得到,具体来说,当 \(a(x, y) = 1\) 时,\(r(x, y) = -1\),否则 \(r(x, y) = r(x, y + 1) + 1\)。边界是 \(r(x, m +1) = -1\)。
那么 \(\texttt{C-}\) 的剩下一部分(先下再右的整个一个折线)有多少种画法呢?我们发现:
- 当 \(\texttt{C-}\) 的一竖延伸到 \((3, 1)\) 时,剩下一部分有 \(r(3, 1) = 3\) 种画法;
- 当 \(\texttt{C-}\) 的一竖延伸到 \((4, 1)\) 时,剩下一部分有 \(r(4, 1) = 0\) 种画法;
- 当 \(\texttt{C-}\) 的一竖延伸到 \((5, 1)\) 时,剩下一部分有 \(r(5, 1) = 5\) 种画法;
- 当 \(\texttt{C-}\) 的一竖延伸到 \((6, 1)\) 时,剩下一部分有 \(r(6, 1) = 1\) 种画法。
因此剩下这部分总共有 \(r(3, 1) + r(4, 1) + r(5, 1) + r(6, 1) = 9\) 种画法。根据乘法原理可以得到,以 \((1, 1)\) 为左上角的 \(\texttt{C-}\) 数量有 \(3 \times 9 = 27\) 个。
一般地,\((x, y)\) 对应的 \(\texttt{C-}\) 数量可以表示为 \(r(x, y) \times \sum\limits_{t = x + 2} ^ k r(t, y)\),其中 \(k\) 满足:\(a(x, y) = a(x + 1, y) = \cdots = a(k, y) = 0\),而 \(a(k + 1, y) = 1\),此处我们认为 \(a(n + 1, y) = 1\)。
这里 \(k\) 的存在是考虑 \(\texttt{C-}\) 的那一竖,有时并不能像上面那个例子一样无限向下延伸,如果遇到一个红色方块就需要停止了。比如,若上面的 \((5, 1)\) 是红色,那么 \((1, 1)\) 对应的 \(\texttt{C-}\) 中,除去上面一横的剩下一部分,只剩下 \(r(3, 1) +r(4, 1) = 3\) 种画法。
为了让式子仍然可以 \(\Theta(1)\) 直接计算,我们考虑预处理 \(g(x, y) = \sum \limits _{t=x} ^ k r(t, y)\),\(k\) 的含义和上面相同。递推和 \(r\) 差不多:当 \(a(x, y) = 1\) 时,\(g(x, y) = 0\),否则 \(g(x, y) = g(x + 1, y) +r(x, y)\)。边界是 \(g(n + 1, y) = 0\)。
这样以来,当 \(a(x, y) = 0\) 且 \(a(x + 1, y) = 0\) 时,\((x, y)\) 对应的 \(\texttt{C-}\) 数量就为 \(r(x, y) \times g(x + 2, y)\),否则显然为 \(0\)。请注意检验 \(a(x + 1, y)\) 为 \(0\) 的必要性。
接下来计算 \(\texttt{F-}\)。还是上面这个例子,上面那一横的画法显然还是 \(r(1, 1) = 3\)。
剩下一部分因为形状的变化,画法数量也会有变化。当 \(\texttt{F-}\) 的上半竖延伸到 \((3, 1)\) 时,第二个横有 \(r(3, 1) = 3\) 种画法,这个仍然不变。但此时我们还要考虑下半竖,总共还有 \(6 - 3 = 3\) 种画法。因此,当 \(\texttt{F-}\) 的上半竖延伸到 \((3, 1)\) 时,除了第一横的剩下一部分总共有 \(3 \times 3 = 9\) 种画法。而当 \(\texttt{F-}\) 上半竖延伸到 \((5, 1)\) 时,总共有 \(r(5, 1) \times (6 - 5) = 5\) 种。其实也就是在 \(\texttt{C-}\) 的基础上,再套一个乘法原理将下半竖的画法统计进去。
类似一般地,\((x, y)\) 对应的 \(\texttt{F-}\) 数量可以表示为 \(r(x, y) \times \sum \limits _{t = x +2} ^ k r(t, y) \times (k - t)\),其中 \(k\) 满足:\(a(x, y) = a(x + 1, y) = \cdots = a(k, y) = 0\),而 \(a(k + 1, y) = 1\),我们认为 \(a(n + 1, y) = 1\)。
预处理 \(h(x, y) = \sum \limits _{t = x} ^ k r(t, y)\),当 \(a(x, y) = 1\) 时,\(h(x, y) = 0\),否则 \(h(x, y) = h(x +1, y) + r(x, y) \times (k - t)\)。边界是 \(h(n +1, y) = 0\)。
这样以来,当 \(a(x, y) = 0\) 且 \(a(x + 1, y) = 0\) 时,\((x, y)\) 对应的 \(\texttt{F-}\) 数量就为 \(r(x, y) \times h(x + 2, y)\),否则显然为 \(0\)。
时间复杂度 \(\Theta(nm)\)。
/*
* @Author: crab-in-the-northeast
* @Date: 2022-12-01 11:11:02
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2022-12-01 12:02:12
*/
#include <bits/stdc++.h>
#define int long long
inline int read() {
int x = 0;
bool f = true;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
if (ch == '-')
f = false;
for (; isdigit(ch); ch = getchar())
x = (x << 1) + (x << 3) + ch - '0';
return f ? x : (~(x - 1));
}
inline std :: pair <std :: string, int> rest(bool space = true) {
std :: string s;
char ch = getchar();
for (; !isgraph(ch); ch = getchar());
for (; isgraph(ch); ch = getchar())
s.push_back(ch);
return {space ? " " + s : s, s.length()};
}
const int maxn = 1005;
const int maxm = 1005;
const int mod = 998244353;
bool a[maxn][maxm];
int r[maxn][maxm], g[maxn][maxm], h[maxn][maxm];
signed main() {
int T = read(); read();
while (T--) {
std :: memset(r, -1, sizeof(r));
std :: memset(g, 0, sizeof(g));
std :: memset(h, 0, sizeof(h));
int n = read(), m = read(), C = read(), F = read();
for (int i = 1; i <= n; ++i) {
std :: string s = rest().first;
for (int j = 1; j <= m; ++j)
a[i][j] = (s[j] == '1');
}
for (int i = 1; i <= n; ++i)
for (int j = m; j; --j)
r[i][j] = a[i][j] ? -1 : (r[i][j + 1] + 1);
for (int i = n; i; --i)
for (int j = 1; j <= m; ++j)
g[i][j] = a[i][j] ? 0 : ((g[i + 1][j] + r[i][j]) % mod);
for (int j = 1; j <= m; ++j) {
for (int i = n, k = n; i; --i) {
if (a[i][j])
k = i - 1;
else
h[i][j] = (h[i + 1][j] + r[i][j] * (k - i)) % mod;
}
}
int c = 0, f = 0;
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= m; ++j) {
if (a[i][j] || a[i + 1][j])
continue;
(c += r[i][j] * g[i + 2][j]) %= mod;
(f += r[i][j] * h[i + 2][j]) %= mod;
}
}
printf("%lld %lld\n", c * C, f * F);
}
return 0;
}