神经形态视觉计算
-
当前问题:
-
spikes vs bits (脉冲 vs 位)
-
meurons vs memory (神经元 vs 计算单元)(真空管vacuum tube,晶体管transistor,忆阻器memristor)
-
synapses vs memory(突触 vs 记忆)
-
distributed and localized vs memory and computing separated (分布式和本地化 vs 内存和计算分离)
-
-
人工智能计算性能与大脑计算性能的对比
- big data(数据),GPU(算力),algorithms(算法)
- 在巨大的算力支撑下,算法显得不那么重要
- 瓶颈:鲁棒性、泛化能力弱(Robustness and generalization),开放环境适应性差(Flexibility)
-
新概念:什么是神经形态计算(Neuromorphic Computing)
- 最开始是制造一个像大脑一样的硬件系统
- 用大脑的结构提升类脑计算的性能,突破现代人工智能的瓶颈
-
需要借鉴大脑的哪些结构
- 神经科学:突触的信息处理机制、突触可塑性(2013诺贝尔生理医学奖),大脑空间认知神经系统(2014诺贝尔生理医学奖),皮层-海马体学习和记忆系统(2017nature,2020science,2020neuron)
- 传统芯片很难支持大量计算
- 硬件实现:脉冲视觉芯片、天机芯片、达尔文芯片等
- 类脑计算(neuromorphic computing)连接神经科学脑科学到硬件之间的桥梁
-
怎样构建桥梁
- 模拟脉冲精确的信号传递+快速传递机制(rapid and precise signaling)大脑以毫秒级传输数据
-
Nonlinearity 神经元的非线性
-
脉冲神经元:非线性,动力学特征(temporal dynamics) 膜电位积分、漏电、不应期、脉冲发放
\(\tau_m\frac{dV_m}{dt}=-V_m+I(t)\)
输入为脉冲信号,输出为脉冲信号
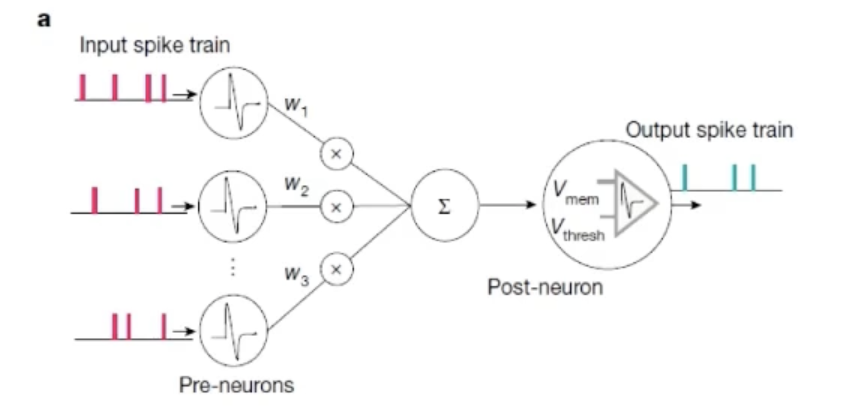
-
人工神经元:ReLU或者Sigmoid激活函数
\(\tau\frac{dV_{mem}}{dt}=-V_{mem}+\frac{\Delta}{i}V_i\omega_i\)
输入为数字信号,输出为数字信号
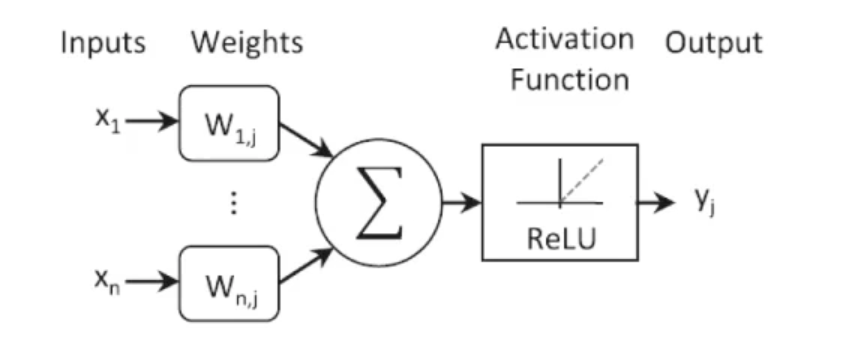
-
-
Wiring连接结构
-
Synaptic plasticity VS back propogation 突触可塑性 VS 反向传播
-
Local learning VS global loss function 局部学习 VS 全局损失函数
-
Hierarchical, parallel VS feedforward, lay-wise 分层、并行 VS 前馈、分层
-
新的问题:大脑能实现误差反向传播吗?(对大脑学习机制的质疑)
生物神经元并不对称,大脑传递与人工神经元并不完全类似
-
-
神经可塑性(Neuronal Plasticity)
- 大脑依赖于多重可塑性(multiple plasticity)和体内平衡机制(homeostasis mechanisms),这些机制作用于突触(synaptic)和细胞内在(cell-instrinsic)的参数
- 脉冲时间依赖(Spike-timing-dependent)的可塑性似乎取决于网络细节活动(details of network activity),超过了平均发射率(average firing rates)
-
学习机制(Learning Rules)
-
Spike-Timing-Dependent-Plasticity(STDP)学习机制
-
调节神经元之间的连接强度,完成深层网络搭建
-
\(a_{di}(-\Delta t)=+A_{di}e^{\frac{\Delta t}{\tau_{di}}}~~~~~if~\Delta<0\)
\(a_{id}(-\Delta t)=-A_{id}e^{-\frac{\Delta t}{\tau_{id}}}~~~if~\Delta>0\)
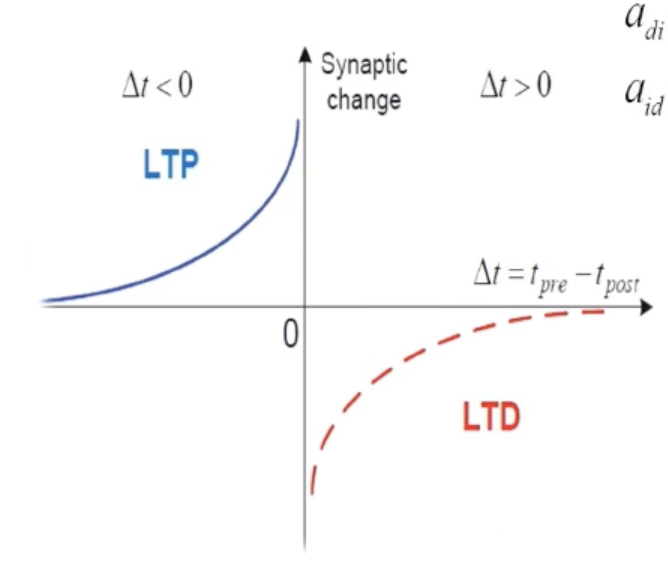
-
-
Supervised Learning-Precise Spike Driven Plasticity 监督学习-精确的脉冲驱动可塑性(PSD)
-
通过将脉冲与核函数卷积,将输入脉冲序列转化为模拟信号
-
突触适应性由期望输出和实际输出之间的误差决定,正的误差叫做LTP,负的误差叫做LTD
-
模型结构;
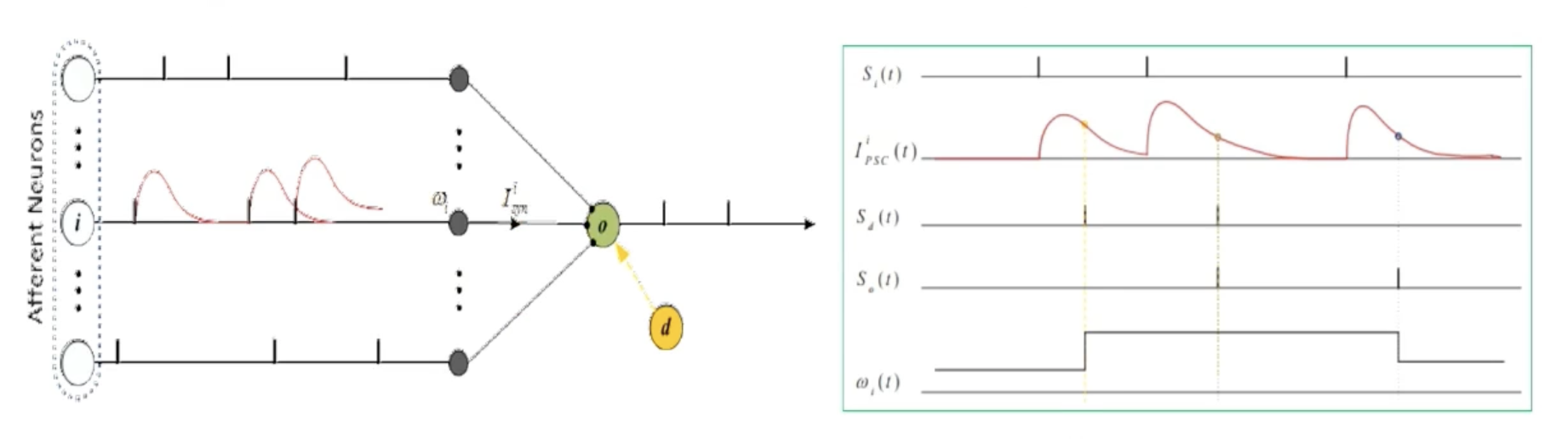
-
Learning rules:源自于常见的Widrow-Hoff算法
-
-