USACO 2018 Feb Solution
目录- USACO 2018 Feb Solution
- 更好的阅读体验戳此进入
- 题面 Luogu 链接
- LG-P4266 [USACO18FEB]Rest Stops S
- LG-P4264 [USACO18FEB]Teleportation S
- LG-P4088 [USACO18FEB]Slingshot P
- LG-P4265 [USACO18FEB]Snow Boots S
- LG-P4269 [USACO18FEB]Snow Boots G
- LG-P4268 [USACO18FEB]Directory Traversal G
- LG-P4267 [USACO18FEB]Taming the Herd G
- LG-P4270 [USACO18FEB]Cow Gymnasts P
- LG-P4271 [USACO18FEB]New Barns P
- UPD
更好的阅读体验戳此进入
题面 Luogu 链接
LG-P4266 [USACO18FEB]Rest Stops S
题面
这题你们基本都读完就能切吧。。真的很水。。
sssmzy 和他的私人教练 zpair 正在徒步攀爬彩虹糖山,我们将其抽象成一条长度为 $ l $ 的长直路径,其中有 $ n $ 个彩虹糖补给站,每个有 $ x_i, c_i $ 分别表示距离 $ 0 $(也就是起点)点的距离和每秒能吃到的彩虹糖数量。sssmzy 会以 $ r_f\texttt{秒/米} $(你没看错)的速度一直前进,zpair 的速度是 $ r_b\texttt{秒/米} $,同时可以选择在某个补给站休息任意秒吃掉对应数量的彩虹糖,因为 zpair 比较年轻,所以保证 $ r_b \lt r_f $,但是因为年轻人比较有活力,所以他必须全程都不在 sssmzy 后面,求 zpair 最多可以吃到多少彩虹糖。
$ 1 \le l \le 10^6, 1 \le n \le 10^5, 1 \le r_b \lt r_f \le 10^6, 1 \le c_i \le 10^6, 0 \lt x_i \lt l $。
$ l, n, r_f, r_b $
$ x_1, c_1 $
$ x_2, c_2 $
$ \cdots $
$ x_n, c_n $
Examples
Input_1
10 2 4 3 7 2 8 1
Output_1
15
Solution
没啥可说的吧?按照 $ c_i $ 排个序,无脑优先选可以选的最高价值的补给站,模拟一下即可,记得开 long long,这个贪心我感觉没有绿色的难度。。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
int L, N;
vector < pair < int, int >/*price, position*/ > rest;
int spdF, spdB;
int d;
ll ans(0);
int main(){
L = read(), N = read(), spdF = read(), spdB = read(); d = spdF - spdB;
for(int i = 1; i <= N; ++i){int p = read(), c = read(); rest.emplace_back(c, p);}
int cur(0); sort(rest.begin(), rest.end(), greater < pair < int, int > >());
for(auto res : rest)
ans += (ll)res.first * max(0, res.second - cur) * d, cur = max(cur, res.second);
printf("%lld\n", ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4264 [USACO18FEB]Teleportation S
题面
数轴上存在 $ n $ 对 $ a_i, b_i $ 表示有一坨牛粪需要从 $ a_i $ 送到 $ b_i $ 并贡献 $ d_i = \vert a_i - b_i \vert $,数轴上存在一个起点为 $ 0 $,终点为 $ y $ 的便便传送门,可以在 $ 0 $ 的贡献下将牛粪从 $ 0 $ 传送到 $ y $,同样贡献为不用传送门走的距离,最小化贡献和,求最小值。
$ 1 \le n \le 10^5, -10^8 \le a_i, b_i \le 10^8 $。
Examples
Input_1
3 -5 -7 -3 10 -2 7
Output_1
10
Solution
这道题告诉我们,题做不出来的时候要多去去厕所,去溜达一圈之后或许就突然想明白了。。
我感觉还算是一道挺有意思的题,比较奇妙,难度适中,蓝色评的也很合理。
显然当 $ y $ 确定后对于每一对 $ a_i, b_i $ 的贡献即为 $ f(y)i = \min(\vert a_i - b_i \vert, \vert a_i \vert + \vert y - b_i \vert) $,我们的答案即为 $ \sum{i = 1}^n f(y)_i $。
此时显然如果有 $ \vert a_i - b_i \vert \lt \vert a_i \vert $,解一下就是 $ a_i \ge b_i \gt 0 \vee 0 \le a_i \lt b_i \lt 2a_i \vee 0 \gt a_i \gt b_i \gt 2a_i \vee a_i \lt b_i \lt 0 $,那么一定不走传送门,也就是选前者,这样的话对于这个 $ f(y)_i $ 就是一条直线,不过这一大坨不等式看着就很阴间,画个图吧:
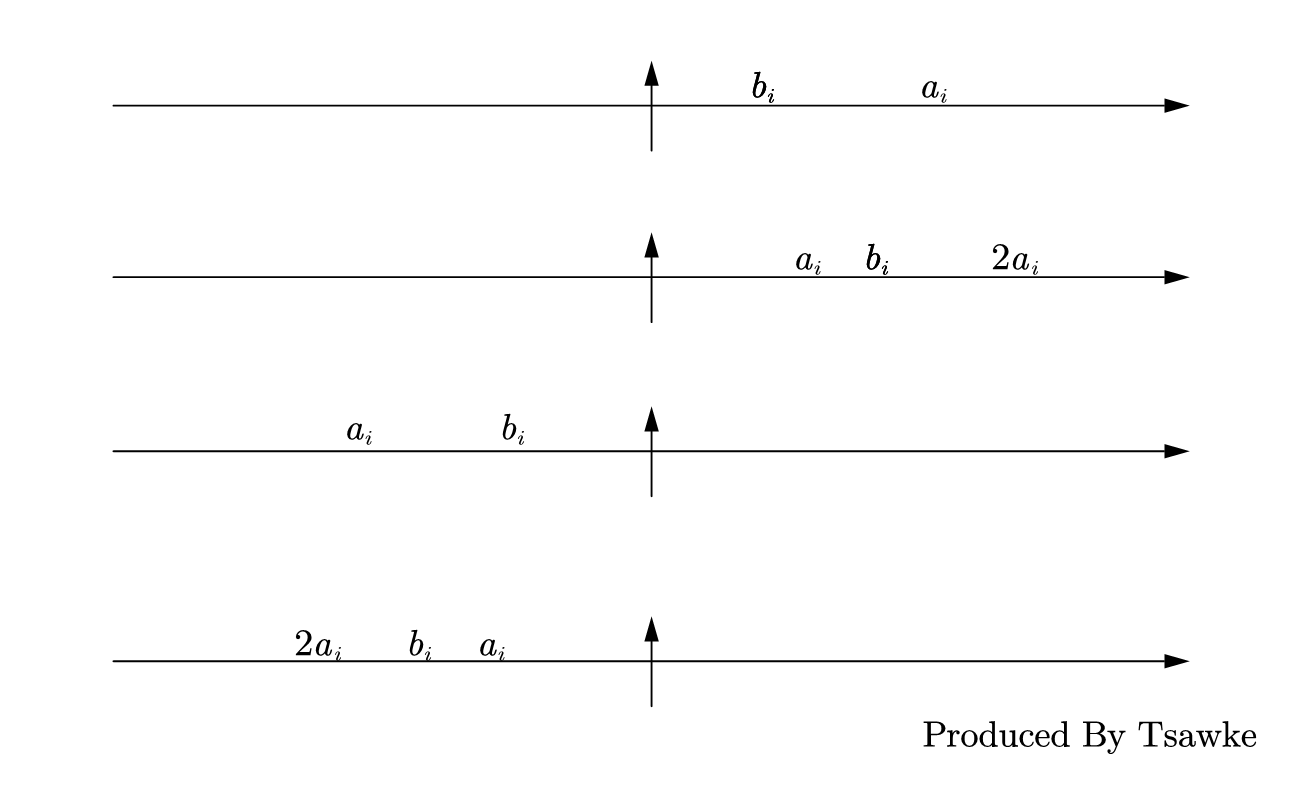
观察发现剩下的可能性就只有 $ 0 \le 2a_i \lt b_i \vee b_i \lt2a_i \le 0 \vee a_i \lt 0 \lt b_i \vee b_i \lt 0 \lt a_i $ 了,而这一段区间则与 $ y $ 相关,需要额外讨论一下。
此时的原式为 $ f(y)_i = \min(\vert a_i - b_i \vert, \vert a_i \vert + \vert y - b_i \vert) $,考虑分类讨论,如在 $ 0 \le 2a_i \lt b_i $ 的条件下,原式转化为 $ \min(b_i - a_i, a_i + \vert y - b_i \vert) $,然后把 $ y $ 和 $ b_i $ 之间的关系讨论一下(这里就很简单了,不多赘述,注意一下 $ b_i \lt 2b_i - 2a_i $ 在条件下恒成立即可),最终可以写成一下柿子:
$ 0 \le 2a_i \lt b_i $:
\[f(y)_i = \left\{ \begin{array}{ll} b_i - a_i &\quad y \in (-\infty, 2a_i] \cup [2b_i - 2a_i, +\infty) \\ -y + a_i + b_i &\quad y \in (2a_i, b_i) \\ y + a_i - b_i &\quad y \in [b_i, 2b_i - 2a_i) \end{array} \right. \]然后在 $ b_i \lt2a_i \le 0 $ 同理可以推出:
$ b_i \lt2a_i \le 0 $:
\[f(y)_i = \left\{ \begin{array}{ll} a_i - b_i &\quad y \in (-\infty, 2b_i - 2a_i] \cup [2a_i, +\infty) \\ -y - a_i + b_i &\quad y \in (2b_i - 2a_i, b_i) \\ y - a_i - b_i &\quad y \in [b_i, 2a_i) \end{array} \right. \]剩下的两个区间也同理推导一下即可:
$ a_i \lt 0 \lt b_i $:
\[f(y)_i = \left\{ \begin{array}{ll} b_i - a_i &\quad y \in (-\infty, 0] \cup [2b_i, +\infty) \\ -y - a_i + b_i &\quad y \in (0, b_i) \\ y - a_i - b_i &\quad y \in [b_i, 2b_i) \end{array} \right. \]$ b_i \lt 0 \lt a_i $:
\[f(y)_i = \left\{ \begin{array}{ll} a_i - b_i &\quad y \in (-\infty, 2b_i] \cup [0, +\infty) \\ -y + a_i + b_i &\quad y \in (2b_i, b_i) \\ y + a_i - b_i &\quad y \in [b_i, 0) \end{array} \right. \]现在我们也就能确定下来每一条 $ f(y)_i $ 的形状了,都是类似下图的形状,只是 “转折点” 不同,和 $ y $ 无关的认为其没有转折点即可。
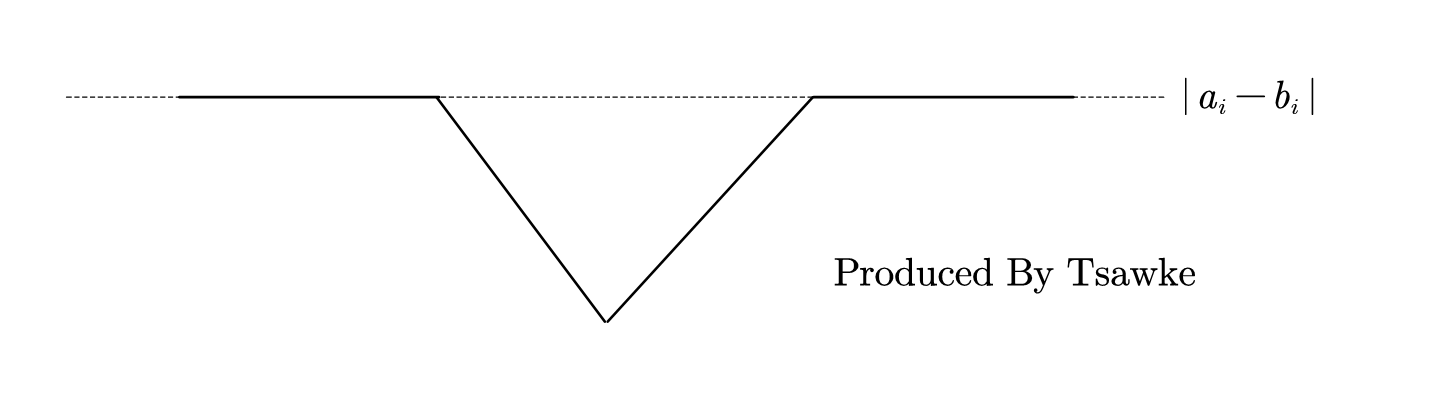
此时我们就需要考虑一下求 $ \sum_{i = 1}^nf(y)_i $ 了。
不难想到 $ O(n) $ 记录一下每一条线的 “转折点” 的位置,建立一个差分数组,然后每条线段斜率变为 $ -1 $ 之后对应位置加上 $ -1 $,斜率变为 $ 1 $ 之后加上 $ 2 $,变回与 $ y $ 相关之后再加上 $ -1 $,然后我们把差分数组做个前缀和,这样当前的前缀和数组的值就是 $ i $ 相对 $ i - 1 $ 的总答案变化量,对于 $ 0 $ 处我们认为其为 $ \sum_{i = 1}^n \vert a_i - b_i \vert $,然后在前缀和上再做一个前缀和,令其为 $ sum_i $,则不难想到答案即为 $ \min{sum_i} $,然后这里因为坐标值域范围很大,所以考虑离散化,为了写着方便,直接开一个 map 存即可,排序也省了。
至此,我们就做完了这道奇怪的大分类讨论,复杂度 $ O(n \log n) $,卡在排序上。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
int N;
ll origin(0);
ll mn(LONG_LONG_MAX);
map < ll, ll > mp;
ll sum[310000]; int cnt(0);
void Insert(int p, int v){
if(mp.find(p) == mp.end())mp.insert({p, v});
else mp[p] += v;
}
void InsertAll(int sp1, int sp2, int sp3){
Insert(sp1, -1);
Insert(sp2, 2);
Insert(sp3, -1);
}
int main(){
N = read();
for(int i = 1; i <= N; ++i){
int a = read(), b = read();
origin += abs(a - b);
if(0 <= 2 * a && 2 * a < b)InsertAll(2 * a, b, 2 * b - 2 * a);
else if(b < 2 * a && 2 * a <= 0)InsertAll(2 * b - 2 * a, b, 2 * a);
else if(a < 0 && 0 < b)InsertAll(0, b, 2 * b);
else if(b < 0 && 0 < a)InsertAll(2 * b, b, 0);
}
ll cur(0), sum(origin); int lft(INT_MIN);
mn = origin;
for(auto v : mp){
sum += (ll)cur * (v.first - lft);
cur += v.second, lft = v.first;
mn = min(mn, sum);
}
printf("%lld\n", mn);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4088 [USACO18FEB]Slingshot P
题面
数轴上存在 $ n $ 个便便弹弓,每个有 $ x_i, y_i, t_i $ 表示该便便弹弓可以用 $ t_i $ 的时间将便便从 $ x_i $ 发射到 $ y_i \(。也可以直接开粪车送便便,\) d $ 距离需要花费 $ d $ 时间。有 $ m $ 个询问,每个有 $ a_i, b_i $,表示求让一坨便便从 $ a_i $ 送到 $ b_i $,最多可以使用一次便便弹弓,最少需要花费多少时间。
$ 1 \le n, m \le 10^5, 0 \le x_i, y_i, t_i, a_i, b_i \le 10^9 $。
Examples
Input_1
2 3 0 10 1 13 8 2 1 12 5 2 20 7
Output_1
4 3 10
Solution
和上一题核心思想差不多,依然考虑,对于询问 $ a, b $,不使用弹弓就是 $ \lvert a - b \rvert $,使用弹弓 $ x, y, t $ 的话结果就是 $ \lvert a - x \rvert + \lvert b - y \rvert + t $,我们需要最小化这个值。
看一下这个柿子实际上就是两个点之间的曼哈顿距离再加上一个值,说人话就是两点之间的横纵坐标差的绝对值之和再加上点 $ (x, y) $ 的点权,然后发现这玩意变成二维数点了。。首先讨论一下绝对值,把绝对值拆掉,离散化,然后按 $ x $ 排序,把合法的塞到权值树状数组里,值就是对应点 $ (x, y) $ 的那些信息,随便搞一下就行了,细节不少。。
然后在具体实现的时候可以不用分类讨论写四个树状数组,直接清空原来的然后将坐标轴旋转一下,可以认为是让对应的大小关系反转,也就是把 $ x $ 和 $ rx $ 取个相反数即可。这里 $ x $ 是离散化之后的值,只保留大小关系,而树状数组上索引需要为正,所以每次 “旋转坐标轴” 的时候需要 $ x \leftarrow -x + lim + 1, rx \leftarrow -rx $,后者不需要转正是因为我们实际上就是把原来的 $ a - x $ 变成 $ x - a $,此时前者为负,后者一定为正。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define NM (N + M)
template< typename T = int >
inline T read(void);
vector < int > data;
struct Node{
int idx;
int x, y;
int rx, ry;
int t;
friend const bool operator < (Node a, Node b){return a.x < b.x;}
}nod[210000];
int N, M;
ll lim;
ll ans[110000];
class BIT{
private:
ll tr[410000];
public:
void clear(void){memset(tr, 0x3f, sizeof tr);}
int lowbit(int x){return x & -x;}
void Modify(int x, ll v){while(x <= lim)tr[x] = min(tr[x], v), x += lowbit(x);}
ll Query(int x){ll ret((ll)INT_MAX * 114514); while(x)ret = min(ret, tr[x]), x -= lowbit(x); return ret;}
}bit;
void Make(void){
sort(nod + 1, nod + NM + 1);
bit.clear();
for(int i = 1; i <= NM; ++i){
if(!~nod[i].t)ans[nod[i].idx] = min(ans[nod[i].idx], bit.Query(nod[i].y) + nod[i].rx + nod[i].ry);
else bit.Modify(nod[i].y, (ll)-nod[i].rx - nod[i].ry + nod[i].t);
}
}
int main(){
memset(ans, 0x3f, sizeof ans);
N = read(), M = read();
for(int i = 1; i <= N; ++i){
int x = read(), y = read(), t = read();
nod[i] = Node{i, x, y, x, y, t};
data.emplace_back(x), data.emplace_back(y);
}
for(int i = 1; i <= M; ++i){
int x = read(), y = read();
nod[i + N] = Node{i, x, y, x, y, -1};
data.emplace_back(x), data.emplace_back(y);
ans[i] = abs(y - x);
}sort(data.begin(), data.end());
data.erase(unique(data.begin(), data.end()), data.end());
lim = data.size();
for(int i = 1; i <= NM; ++i)
nod[i].x = distance(data.begin(), lower_bound(data.begin(), data.end(), nod[i].x) + 1),
nod[i].y = distance(data.begin(), lower_bound(data.begin(), data.end(), nod[i].y) + 1);
Make();
for(int i = 1; i <= NM; ++i)
nod[i].x = -nod[i].x + lim + 1, nod[i].rx = -nod[i].rx;
Make();
for(int i = 1; i <= NM; ++i)
nod[i].y = -nod[i].y + lim + 1, nod[i].ry = -nod[i].ry;
Make();
for(int i = 1; i <= NM; ++i)
nod[i].x = -nod[i].x + lim + 1, nod[i].rx = -nod[i].rx;
Make();
for(int i = 1; i <= M; ++i)printf("%lld\n", ans[i]);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4265 [USACO18FEB]Snow Boots S
题面
给定序列 $ f_n $ 表示位置 $ i $ 的积雪深度,保证 $ f_1 = f_n = 0 $,共有 $ b $ 双靴子,每双有 $ s_i, d_i $,表示最大可承受 $ s_i $ 深度的积雪,可以走 $ d_i $ 的距离。zpair 可以在任意时刻丢掉序列最前面的一双靴子或者丢掉脚上的换上序列最前面的一双靴子,换靴子时必须保证其身上的和换上的可承受深度都要大于当前位置积雪深度,且穿着某双靴子走的路程必须不大于 $ d_i $,最小化走到 $ n $ 需要丢掉的靴子数,求最小值。
Tips:zpair 每次走 $ d_i $ 距离时中间的积雪深度可以大于 $ s_i $,保证起始和终点满足条件即可(这也是我理解错的地方)。
$ 2 \le n, b, \le 250, 0 \le f_i, s_i \le 10^9, 1 \le d_i \le n $。
Examples
Input_1
10 4 0 2 8 3 6 7 5 1 4 0 2 3 4 2 3 4 7 1
Output_1
2
Solution
题目读完没啥好思路,然后一看数据范围 $ 250 $,直接就口糊了一个 $ \texttt{2D2D} $ 的 dp,然后感觉 $ 250^4 $ 过不了,所以 “讨论” 了一下优化成了状态 $ O(nb) $ 转移 $ O(b \log n) $ 最终 $ O(b^2 n \log n) $ 的肯定能过的做法,然后发现把这玩意变成预处理直接就是 $ O(n^2b + nb^2) $ 了,显然能过。大致思路是令 $ pre(i, j) $ 表示第 $ i $ 双靴子在 $ j $ 的位置上最多可以走 $ j $ 和 $ j $ 以前最长多远,或者也可以认为是求前缀里最后一个大于当前数的位置 $ +1 $,这东西 $ O(n^2b) $ 就完事了,然后考虑令 $ dp(i, j) $ 表示用前 $ i $ 双靴子并钦定用 $ i $,走到 $ j $ 位置是否可以到达(最开始设的是至少需要丢弃多少,但是实际上 $ i - 1 $ 就是答案,记录能否到达即可),这玩意大概就是枚举上一个用的靴子,然后用 $ pre $ 转移一下即可,复杂度是 $ O(nb^2) $ 的,当然我的方程写的有点小问题(正确性好像也有点问题),不过也没必要调,这个东西很不优而且边界不好设置。
考虑正解,$ \texttt{2D2D} $ 的 dp 能过。。状态不变,考虑转移的时候枚举换的下一双鞋和走到的位置,然后加点剪枝就过了。对于复杂度正确的方法可以把状态变成 $ dp(i) $ 表示前 $ i $ 能走多远之类的,变成 $ \texttt{1D2D} $ 的就行了。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
int N, B;
int dep[300];
int s[300], d[300];
bool dp[300][300];
// int dp[300][300];
// int pre[300][300];
int main(){
// memset(dp, 0x3f, sizeof dp);
// for(int i = 0; i <= 260; ++i)dp[i][0] = i;
dp[1][1] = 1;
N = read(), B = read();
for(int i = 1; i <= N; ++i)dep[i] = read();
for(int i = 1; i <= B; ++i)s[i] = read(), d[i] = read();
// Waiting for debugging...
// for(int i = 1; i <= B; ++i)
// for(int j = 1; j <= N; ++j)
// for(int k = j; k >= 1; --k)
// if(dep[k] <= s[i] && j - k + 1 <= d[i])pre[i][j] = k;
// else break;
// for(int i = 1; i <= B; ++i)
// for(int j = 1; j <= N; ++j)
// if(dep[j] <= s[i])
// for(int k = i - 1; k >= 0; --k)
// if(pre[i][j])dp[i][j] = min(dp[i][j], dp[k][pre[i][j] - 1] + i - k - 1);
// int mn(INT_MAX);
// for(int i = 1; i <= B; ++i)mn = min(mn, dp[i][N]);
// printf("%d\n", mn);
for(int i = 1; i <= B; ++i)
for(int j = 1; j <= N; ++j)
if(dp[i][j])
for(int k = i; k <= B; ++k)
if(s[k] >= dep[j])
for(int l = j + 1; l <= min(N, j + d[k]); ++l)
if(s[k] >= dep[l])
dp[k][l] = true;
for(int i = 1; i <= B; ++i)if(dp[i][N])printf("%d\n", i - 1), exit(0);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4269 [USACO18FEB]Snow Boots G
题面
给定长度为 $ n $ 的序列 $ f_n \(,\) b $ 组询问每次 $ s_i, d_i $,求 $ f_n $ 中是否存在一段连续的长度超过 $ d_i $ 且每个数均大于 $ s_i $ 的子串,不存在输出 $ 1 $,存在输出 $ 0 $。
$ 1 \le n, b \le 10^5, 0 \le f_i, s_i \le 10^9, 1 \le d_i \le n - 1 $。
Examples
Input_1
8 7 0 3 8 5 6 9 0 0 0 5 0 6 6 2 8 1 10 1 5 3 150 7
Output_1
0 1 1 0 1 1 1
Solution
题面简化之后一个很显然的做法就是线段树,认为叶子节点符合要求的时候就是 $ 1 $,不符合要求为 $ 0 $,每次等于是一些单点修改,然后整个区间查询最长的连续 $ 1 $ 的串(这东西很简单吧,维护最长串,左侧最长串,右侧最长串即可)当然嗯搞肯定不行,所以考虑把序列和询问都离线下来降序排个序,这样的话对于上一个询问不符合的 $ f_i $ 一定这次也不符合,也就变成了一个类似双指针的东西,这样我们就可以让修改次数变成 $ O(n) $ 的,然后这样线段树做法的话就是 $ O(n \log n + q \log q) $。然后线段树码量比较大,所以考虑直接用双向链表,维护一下当前有多长的不符合条件的子串就行了,不难实现,注意为了更方便求链表之间在原来位置的距离,用数组模拟链表会更方便,复杂度卡在排序上,但是求解变成 $ O(n + q) $ 了。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
// struct List{
// List *pre, *nxt;
// int dep;
// };
// List* lst[110000];
struct List{
int pre, nxt;
int dep;
}lst[110000];
int N, B;
struct Snow{
int idx, dep;
friend const bool operator < (const Snow &a, const Snow &b){return a.dep > b.dep;}
}snow[110000];
struct Boot{
int idx, dis, dep;
friend const bool operator < (const Boot &a, const Boot &b){return a.dep > b.dep;}
}boot[110000];
bool ans[110000];
int main(){
N = read(), B = read();
for(int i = 1; i <= N; ++i){
// lst[i]->dep = read();
// if(i != 1)lst[i]->pre = lst[i - 1];
// if(i != N)lst[i]->nxt = lst[i + 1];
snow[i] = Snow{i, read()};
lst[i] = List{i - 1, i + 1, snow[i].dep};
}
for(int i = 1; i <= B; ++i){int s = read(), d = read(); boot[i] = Boot{i, d, s};}
sort(snow + 1, snow + N + 1), sort(boot + 1, boot + B + 1);
int cur(0), mx(0);
for(int i = 1; i <= B; ++i){
while(cur <= N - 1 && snow[cur + 1].dep > boot[i].dep){
++cur;
lst[lst[snow[cur].idx].nxt].pre = lst[snow[cur].idx].pre;
lst[lst[snow[cur].idx].pre].nxt = lst[snow[cur].idx].nxt;
mx = max(mx, lst[snow[cur].idx].nxt - lst[snow[cur].idx].pre);
}if(mx <= boot[i].dis)ans[boot[i].idx] = true;
}
for(int i = 1; i <= B; ++i)printf("%d\n", ans[i] ? 1 : 0);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4268 [USACO18FEB]Directory Traversal G
题面
sssmzy 在他的电脑中存储了很多学习资料,我们都知道在系统大多数路径中都存在名为 .. 的路径,通过此路径可以回到上一级(通过 . 和 .. 等连接的一般叫做相对路径)。给定一些文件夹和文件之间的关系,sssmzy 可以处于某个文件夹中,他要访问所有的文件,显然这些文件相对于其所在文件夹会有很多路径,你需要最小化每个文件路径长度和,并输出。特别地,我们不考虑使用 ./。
$ 2 \le n \le 10^5 $。
对于样例,其文件之间的结构为:
bessie/ --folder1/ ----file1 ----folder2/ ------file2 --folder3/ ----file3 --file4
可以证明从 folder2 出发会有最小路径长度和,路径为:
../file1 file2 ../../folder3/file3 ../../file4
关于输入格式:
第一行包含一个整数N(\(2 \leq N \leq 100,000\)),为所有文件和文件夹的总数量。为了便于输入,每个对象(文件或文件夹)被赋予一个唯一的 $ 1 $ 至 $ N $ 之间的 ID,其中 ID 1 指的是顶层文件夹。
接下来有 $ N $ 行。每行的第一项是一个文件或是文件夹的名称。名称仅包含小写字母 $ a-z $ 和数字 $ 0-9 $,长度至多为 $ 16 $ 个字符。名称之后是一个整数 $ m $。如果 $ m $ 为 $ 0 $,则该对象是一个文件。如果 $ m > 0 $,则该对象是一个文件夹,并且该文件夹下共有 $ m $ 个文件或文件夹。在 $ m $ 之后有 $ m $ 个整数,为该文件夹下的对象的 ID。
Examples
Input_1
8 bessie 3 2 6 8 folder1 2 3 4 file1 0 folder2 1 5 file2 0 folder3 1 7 file3 0 file4 0
Output_1
42
Solution
一个有点像换根 DP 但是没换根的树形 DP。
首先根据定义,显然不会有空文件夹,所以叶子节点均为文件夹。
首先以根目录的文件夹为根 dfs 一遍,记录一大堆东西,以根目录为根的路径长度和 $ f(x) $,其自身文件名长度 $ \omega(x) \((不包括 `/`),特别地,\) \omega(root) = 0 $,以 $ root $ 为根 $ x $ 所在子树叶子节点数量 $ leaf(x) $。
然后再做一遍不换根的换根 DP,同样深搜,令子节点答案为 $ f(y) $,父节点为 $ f(x) $,显然有 $ f(y) = f(x) - leaf(y) \times (\omega(y) + 1) + (leaf(root) - leaf(y)) \times 3 $。
至于 $ \times 3 $ 就是 ../,不难理解吧,这样跑一遍求一下最大的 $ f(x) $ 就行。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
struct Edge{
Edge* nxt;
int to;
OPNEW;
}ed[210000];
ROPNEW(ed);
Edge* head[110000];
int N;
ll f[110000];
int leaf[110000], w[110000];
ll dis[110000];
ll mn;
void dfs_pre(int p = 1, int fa = 0){
if(p != 1 && !head[p]->nxt)leaf[p] = 1, f[1] += dis[fa] + w[p];
else dis[p] = p == 1 ? 0 : dis[fa] + w[p] + 1;
for(auto i = head[p]; i; i = i->nxt)if(SON != fa)dfs_pre(SON, p), leaf[p] += leaf[SON];
}
void dfs(int p = 1, int fa = 0){
if(p != 1 && head[p]->nxt)f[p] = f[fa] - (ll)leaf[p] * (w[p] + 1) + (ll)(leaf[1] - leaf[p]) * 3, mn = min(mn, f[p]);
for(auto i = head[p]; i; i = i->nxt)if(SON != fa)dfs(SON, p);
}
int main(){
N = read();
for(int i = 1; i <= N; ++i){
string dir;
cin >> dir;
w[i] = i == 1 ? 0 : (int)dir.size();
int M = read();
for(int j = 1; j <= M; ++j){
int son = read();
head[i] = new Edge{head[i], son};
head[son] = new Edge{head[son], i};
}
}
dfs_pre();
mn = f[1];
dfs();
printf("%lld\n", mn);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4267 [USACO18FEB]Taming the Herd G
题面
原题面说的很奇怪,我理解了半天才看懂,所以这题就不简化题面了。。
一大清早,Farmer John就被木材破裂的声音吵醒了。是这些奶牛们干的,她们又逃出牛棚了!
Farmer John已经厌烦了奶牛在清晨出逃,他觉得受够了:是时候采取强硬措施了。他在牛棚的墙上钉了一个计数器,追踪从上次出逃开始经过的天数。所以如果某一天早上发生了出逃事件,这一天的计数器就为\(0\);如果最近的出逃是\(3\)天前,计数器读数就为\(3\)。Farmer John一丝不苟地记录了每一天计数器的读数。年末到了,Farmer John准备做一些统计。他说,你们这些奶牛会付出代价的!然而他的某些记录看上去不太对劲……
Farmer John想要知道从他开始记录以来发生过多少次出逃。但是,他怀疑这些奶牛篡改了它的记录,现在他所确定的只有他是从发生出逃的某一天开始记录的。请帮助他求出,对于每个从他开始记录以来可能发生的出逃次数,他被篡改了的记录条数的最小值。
输入格式(文件名:taming.in):
输入的第一行包含一个整数\(N\)(\(1 \leq N \leq 100\)),表示从Farmer John开始对奶牛出逃计数器进行计数以来已经经过的天数。
第二行包含\(N\)个空格分隔的整数。第\(i\)个整数是一个非负整数\(a_i\)(不超过\(100\)),表示在第\(i\)天计数器的数字是\(a_i\),除非奶牛篡改了这一天的记录条目。输出格式(文件名:taming.out):
输出包含\(N\)个整数,每行一个。第\(i\)个整数为所有发生\(i\)次出逃的事件序列中,与该事件序列不一致的记录条目条数的最小值。
阳间题面:
题目说在一个牛棚里有一个计数器,用来记录每一天有没有奶牛逃跑。
假设今天是第 i 天,如果今天有奶牛逃跑,那么计数器就为 0 。
如果在第 i−j 天有奶牛逃跑,那么计数器就为 j 。
但是记录有可能被篡改,给定一个记录的数列(有可能被篡改过),求在有 i 个奶牛逃跑时的最小被篡改量。
Input_1
6 1 1 2 0 0 1
Output_1
4 2 1 2 3 4
Solution
一道比较裸的 DP,难度在于理解题意。
令 $ dp(i, j) $ 表示前 $ i $ 个数里共跑了 $ j $ 头奶牛,钦定 $ i $ 一定跑了一头牛,然后 $ \texttt{2D2D} $ 的 dp 就出来了,$ dp(k, j) = \min{dp(i, j - 1) + cal(i + 1, k)} \(,\) i \lt k \le n $。可以预处理优化到 $ \texttt{2D1D} $,但是没必要。。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
template< typename T = int >
inline T read(void);
int N;
int a[110];
int dp[110][110];
int cal(int s, int t){
int cnt(0);
for(int i = s; i <= t; ++i)if(a[i] != i - s)++cnt;
return cnt;
}
int main(){
memset(dp, 0x3f, sizeof dp);
dp[0][0] = 0;
N = read();
for(int i = 1; i <= N; ++i)a[i] = read();
for(int i = 0; i <= N; ++i)
for(int j = 1; j <= N; ++j)
for(int k = i + 1; k <= N; ++k)
dp[k][j] = min(dp[k][j], dp[i][j - 1] + cal(i + 1, k));
for(int i = 1; i <= N; ++i)printf("%d\n", dp[N][i]);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4270 [USACO18FEB]Cow Gymnasts P
题面
存在 $ n $ 个平台环形排列,每个平台可以放置 $ [1, n] $ 头奶牛,每次操作时,对于第 $ i $ 层的奶牛,会顺时针移动 $ i - 1 $ 个平台并落下,求有多少种排列能使无论多少次操作每个平台的奶牛数都不改变。
$ 1 \le n \le 10^{12} $。
对于样例,有 $ (1, 1, 1, 1), (2, 2, 2, 2), (3, 3, 3, 3), (4, 4, 4, 4), (2, 3, 2, 3), (3, 2, 3, 2) $。
Examples
Input_1
4
Output_1
6
Solution
一道纯粹的人类智慧题。。。
然后我们这里定义的循环周期并不是一般圆周运动绕一圈的操作次数,而是一头原来在第 $ i $ 层且最高为 $ \xi $ 层的牛再次到第 $ i $ 层且最高为 $ \xi $ 层所需要的旋转次数。也就是对于一个合法的排列,两个同一高度平台之间的距离即为平台内所有牛的循环周期。
首先对于符合条件的排列,有好几个奇怪的性质:
- 对于第 $ i $ 层的奶牛,只能是从其他平台第 $ i $ 层的奶牛平移过来,而不可以是从更高层的奶牛掉下来。
证明:因为是符合条件的排列,我们假设序列中最高的层数为 $ m $,那么一定是前面的 $ m - 1 $ 个平台各自给这个平台贡献一头奶牛,因为如果有往前数第 $ m $ 个的贡献,那么那个平台至少要有 $ m + 1 $ 头奶牛,矛盾。如果在前 $ m - 1 $ 里有至少任意一个没有贡献,那么当前这个台子奶牛就会少至少一个,也矛盾,所以简单想一下刚才的过程,前面第一个贡献当前的第 $ 2 $ 层,第二个贡献第 $ 3 $ 层,$ \cdots $,第 $ m - 1 $ 个贡献当前的第 $ m $ 层,而第 $ m - 1 $ 个能移动 $ m - 1 $ 那么其长度也就必须至少为 $ m $,然后以此类推即可证明所有层数都是由对应层数平移过来的,得证。
- 对于第 $ i $ 层奶牛的循环周期(定义参考伊始)是 $ i $ 的约数。
证明:显然某一时刻第 $ i $ 层的某头奶牛一定是这层的周期为 $ T_i $ 的奶牛移动 $ k $ 次到达的,即 $ i = kT_i $,得证。
- 第 $ i - 1 $ 层奶牛循环周期是第 $ i $ 层奶牛循环周期的约数。
证明:考虑由性质一,第 $ i $ 层的奶牛一定还会到第 $ i $ 层,而到达的位置的第 $ i $ 层已经跑了,所以一定是有 $ i - 1 $ 层的奶牛一直垫着它走的,否则便会掉到小于 $ i $ 的位置了,所以下层的周期一定是上层的约数,即 $ T_{i - 1} \mid T_i $,得证。
- 任意两个平台之间的奶牛数量差不超过 $ 1 $。
证明:由性质二不难得出 $ T_i \mid i, T_{i + 1} \mid i + 1 $,由性质三不难得出 $ T_{i} \mid T_{i + 1} $,又 $ \gcd(i, i + 1) = 1 $,那么显然 $ \gcd(T_i, T_{i + 1}) = 1 $,两数互质,前者又是后者的约数,所以显然前者为 $ 1 $,所以 $ T_1 = T_2 = \cdots = T_{n - 1} = 1 $。所以对于某个层数最高为 $ i $ 的,每次位移的距离是 $ i - 1 $,周期又为 $ 1 $,那么每隔 $ i - 1 $ 个就是相同的层数,这东西不难想到就是任意两者之间差不超过 $ 1 $.
以此我们便可以得出结论:
\[ans = 2 - n + \sum_{i = 1}^{n - 1}2^{\gcd(n, i)} \]证明:首先枚举层数最小的平台有 $ i $ 层,不难想到对于最小平台有 $ i $ 层时,循环周期一定是 $ i $ 的约数,且一共有 $ n $ 个平台,那么循环周期也一定为 $ n $ 的约数,以此不难想到,此时最大的循环周期为 $ \gcd(n, i) $,此时我们举个 $ n = 6, i = 3, \gcd = 3 $ 的例子:
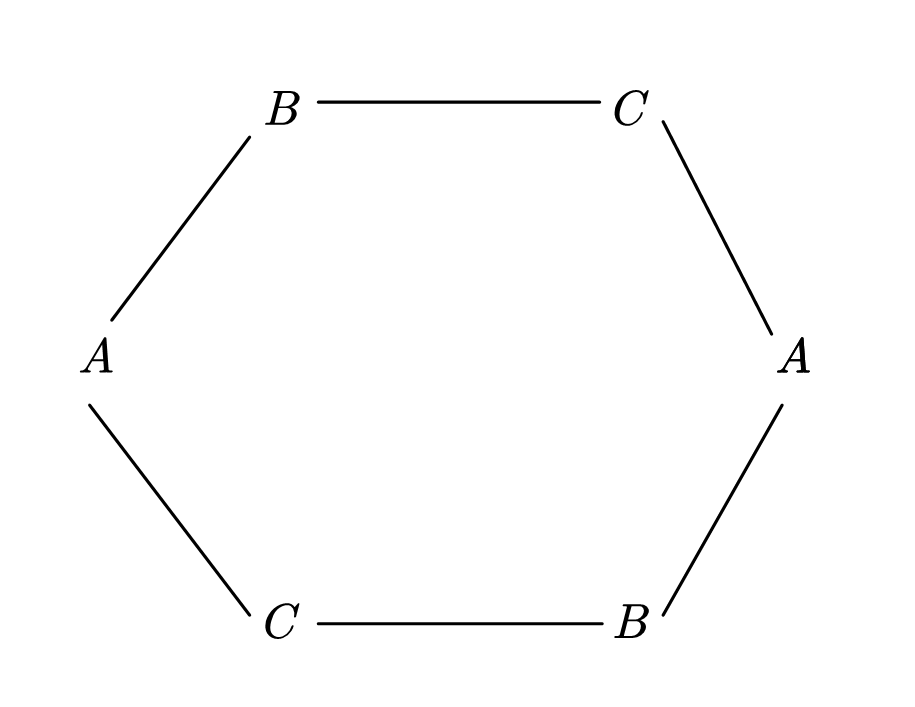
此时根据我们前面的性质一定有标号相同的点值相同,那么此时 $ 2^{\gcd(n, i)} $ 就代表着枚举 $ A, B, C $ 是否为 $ i $,但是此时如果三个值均非 $ i $ 的话,最小值便不能保证为 $ i $,此时还需要对此次的贡献 $ -1 $。
然后此时我们还要考虑,为什么仅枚举是否为 $ i $ 就可以不重不漏了,考虑如钦定 $ A = i $ 时,且钦定 $ B $ 不为 $ i $,则 $ B $ 一定为 $ i + 1 $ 或 $ i - 1 $,后者则最小值会变化,不合法,所以如果不是 $ i $ 那么一定是 $ i + 1 $。所以此时如果还钦定 $ C $ 不是 $ i $,那么它要么是 $ i + 1 $ 要么是 $ i + 2 $,而 $ C $ 与下一个 $ A $ 相连,$ i + 2 $ 和 $ i $ 的差大于 $ 1 $ 了,也不合法。当然我们考虑 $ i + 2 = 5 $,由性质二,发现 $ 3 \nmid 5 $,也不合法,所以仍然为 $ i + 1 $。那么对于这个例子,显然一个数要么是 $ i $ 要么不是,不是的时候数也唯一确定,故可以如此枚举。
随便举几个例子可以发现这个结论似乎正确,那么我们现在尝试严谨一点地去证明,有结论,对于所有非 $ i $ 的点的值一定均为 $ i + 1 $。
首先考虑如果有非 $ i $ 的点,那么一定至少要有一个 $ i + 1 $,这个从我们之前的证明即可得出,因为差最大为 $ 1 $,又不可以是 $ i - 1 $。此时如果后面的值是 $ i + 2 $,那么显然此时 $ T_{i + 1} \ge 2 $,并且此时因为存在 $ i + 2 $,那么最大值一定不是 $ i + 1 $,所以从性质四的证明过程可以得到 $ T_{i + 1} = 1 $,显然矛盾。而如果所有非 $ i $ 均为 $ i + 1 $,那么 $ i + 1 $ 即为最大值,观察性质发现有且仅有最大值是可以不符合恒等于 $ 1 $ 的条件的,所以这样才是合法的。故得证。
所以换一个说法理解,我们枚举的便为此处是 $ i $ 还是 $ i + 1 $,且不能均为 $ i + 1 $,此时贡献为 $ 2^{\gcd(n, i)} - 1 $,考虑如果 $ i = n $,那么不存在 $ i + 1 $ 了,此时需要特判,不难想到最小为 $ n $ 最大为 $ n $ 那么全是 $ n $ 则为唯一的方案,如此最终答案便为:
\[\begin{aligned} ans &=\sum_{i = 1}^{n - 1}(2^{\gcd(n, i)} - 1) + 1 \\ &=2 - n + \sum_{i = 1}^{n - 1}2^{\gcd(n, i)} \\ &=2 - n - 2^n + \sum_{i = 1}^{n}2^{\gcd(n, i)} \end{aligned} \]然后发现数据范围这个柿子肯定过不去,于是考虑优化,继续推柿子:
\[\begin{aligned} \sum_{i = 1}^{n}2^{\gcd(n, i)} &= \sum_{j = 1}^n 2^j \sum_{i = 1}^{n}[\gcd(n, i) = j] \\ &= \sum_{j = 1}^n 2^j \sum_{i = 1}^{n}[j \mid i \land j \mid n \land \gcd(\dfrac{n}{j}, \dfrac{i}{j}) = 1] \\ &= \sum_{j = 1}^n (2^j \times \varphi(\dfrac{n}{j}) \times [j \mid n]) \\ &= \sum_{j \mid n} (2^j \times \varphi(\dfrac{n}{j})) \\ &= \sum_{j \mid n} (2^{\frac{n}{j}} \times \varphi(j)) \end{aligned} \]这个式子应该是可以继续推下去直到严格 $ O(\sqrt{n}\log n) $ 的,但是没必要,到目前这个形式就已经可以通过精细实现打倒这个复杂度了。我们发现如果无脑枚举,找因数是 $ O(\sqrt{n}) $ 的,每个因数求欧拉函数也是 $ O(\sqrt{n}) $ 的,最后会退化成 $ O(n) $,线性筛之类的更不行了,如果可以的话或许 Min25筛 之类的科技可以 $ O(n^{\frac{2}{3}}) $ 实现,刚好能过,不过 duck 不必。
显然我们可以通过分解质因数求欧拉函数,具体地,令 $ p_i $ 为质数且 $ c_i \neq 0 $,如果有:
\[n = \prod_{i = 1}^k p_i^{c^i} \]那么:
\[\varphi(n) = n \times \prod_{i = 1}^k \dfrac{p_i - 1}{p_i} \]然后我们答案式子枚举的是 $ n $ 的因子,显然可以通过枚举其所有质因子不重不漏地凑出来所有的因子,于是写个朴素搜索,暴力枚举每个因子有多少个,以及当前的乘积,和存在的质因子的乘积等等,如此便可以 $ O(1) $ 求出每个需要的欧拉函数,复杂度为因数个数,即 $ O(\sqrt{n}) $,然后剩下的 $ \log $ 复杂度是因为求 $ 2^j $ 的时候快速幂的复杂度,理论上用左移会更优,但是可能爆 long long。然后过程中是需要先让 $ n \div \prod p_i $ 然后再乘 $ \prod p_i - 1 $,否则会爆 long long,当然像我一样直接用 __int128_t 可以直接忽略这些问题。
至此此题解决,还是很精妙的。
Code
#define _USE_MATH_DEFINES
#include <bits/extc++.h>
#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}
using namespace std;
using namespace __gnu_pbds;
mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}
typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;
#define MOD (ll)(1e9 + 7)
template< typename T = int >
inline T read(void);
ll N;
int tot(0);
pair < ll, int > fact[1100000];
int cur[1100000];
__int128_t ans(0);
__int128_t qpow(ll a, ll b){
__int128_t ret(1), mul(a);
while(b){
if(b & 1)ret = ret * mul % MOD;
b >>= 1;
mul = mul * mul % MOD;
}return ret;
}
void dfs(int p = 1, ll base = 1, __int128_t phi = 1, __int128_t div = 1){
if(p > tot){
phi *= base, phi /= div, phi %= MOD;
ans = (ans + phi * qpow(2, N / base) % MOD) % MOD;
return;
}
dfs(p + 1, base, phi, div);
phi *= fact[p].first - 1;
div *= fact[p].first;
for(int i = 1; i <= fact[p].second; ++i)
base *= fact[p].first, dfs(p + 1, base, phi, div);
}
int main(){
N = read < ll >();
ll tmp(N); ll cur(2), cnt(0);
while(tmp > 1){
if(cur * cur > tmp)break;
while(tmp % cur == 0)tmp /= cur, ++cnt;
if(cnt)fact[++tot] = {cur, cnt}, cnt = 0;
++cur;
}if(tmp > 1)fact[++tot] = {tmp, 1};
dfs();
ans = ((((ans + 2 - N) % MOD) - qpow(2, N)) % MOD + MOD) % MOD;
printf("%lld\n", (ll)ans);
fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
return 0;
}
template < typename T >
inline T read(void){
T ret(0);
short flag(1);
char c = getchar();
while(c != '-' && !isdigit(c))c = getchar();
if(c == '-')flag = -1, c = getchar();
while(isdigit(c)){
ret *= 10;
ret += int(c - '0');
c = getchar();
}
ret *= flag;
return ret;
}
LG-P4271 [USACO18FEB]New Barns P
题面
奇怪题,先咕着,laterrrrrr 再来写。
Examples
Input_1
Output_1
Solution
Code
UPD
update-2022_11_10 初稿
标签:le,Feb,int,题解,void,ret,2018,return,define From: https://www.cnblogs.com/tsawke/p/16945853.html