标签：LG le vert int 题解 Teleportation lt 2a quad

LG-P4264 [USACO18FEB]Teleportation S Solution

目录

• LG-P4264 [USACO18FEB]Teleportation S Solution
  • 更好的阅读体验戳此进入
    • 题面
    • Solution
    • Code
  • UPD

更好的阅读体验戳此进入

题面

数轴上存在 $ n $ 对 $ a_i, b_i $ 表示有一坨牛粪需要从 $ a_i $ 送到 $ b_i $ 并贡献 $ d_i = \vert a_i - b_i \vert $，数轴上存在一个起点为 $ 0 $，终点为 $ y $ 的便便传送门，可以在 $ 0 $ 的贡献下将牛粪从 $ 0 $ 传送到 $ y $，同样贡献为不用传送门走的距离，最小化贡献和，求最小值。

$ 1 \le n \le 10^5, -10^8 \le a_i, b_i \le 10^8 $。

Solution

这道题告诉我们，题做不出来的时候要多去去厕所，去溜达一圈之后或许就突然想明白了。。

我感觉还算是一道挺有意思的题，比较奇妙，难度适中，蓝色评的也很合理。

显然当 $ y $ 确定后对于每一对 $ a_i, b_i $ 的贡献即为 $ f(y)i = \min(\vert a_i - b_i \vert, \vert a_i \vert + \vert y - b_i \vert) $，我们的答案即为 $ \sum{i = 1}^n f(y)_i $。

此时显然如果有 $ \vert a_i - b_i \vert \lt \vert a_i \vert $，解一下就是 $ a_i \ge b_i \gt 0 \vee 0 \le a_i \lt b_i \lt 2a_i \vee 0 \gt a_i \gt b_i \gt 2a_i \vee a_i \lt b_i \lt 0 $，那么一定不走传送门，也就是选前者，这样的话对于这个 $ f(y)_i $ 就是一条直线，不过这一大坨不等式看着就很阴间，画个图吧：

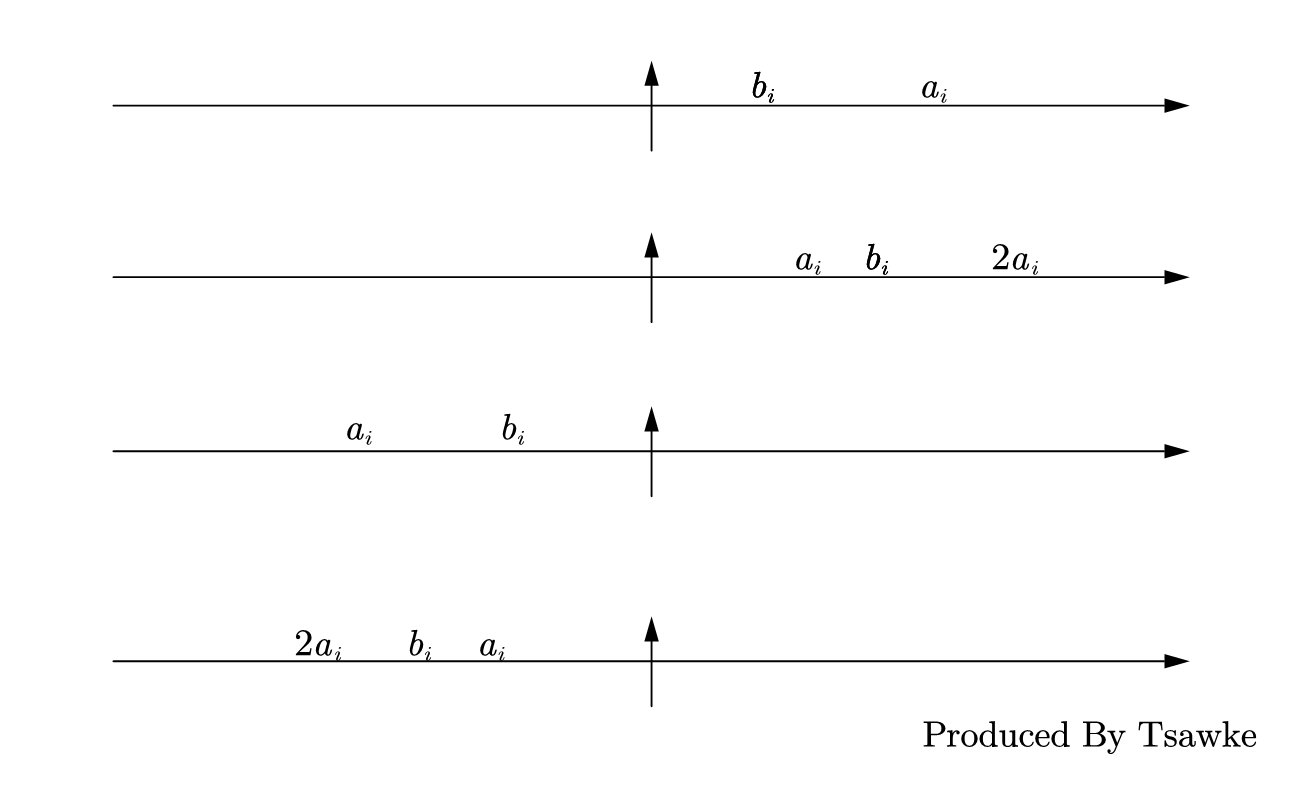
观察发现剩下的可能性就只有 $ 0 \le 2a_i \lt b_i \vee b_i \lt2a_i \le 0 \vee a_i \lt 0 \lt b_i \vee b_i \lt 0 \lt a_i $ 了，而这一段区间则与 $ y $ 相关，需要额外讨论一下。

此时的原式为 $ f(y)_i = \min(\vert a_i - b_i \vert, \vert a_i \vert + \vert y - b_i \vert) $，考虑分类讨论，如在 $ 0 \le 2a_i \lt b_i $ 的条件下，原式转化为 $ \min(b_i - a_i, a_i + \vert y - b_i \vert) $，然后把 $ y $ 和 $ b_i $ 之间的关系讨论一下（这里就很简单了，不多赘述，注意一下 $ b_i \lt 2b_i - 2a_i $ 在条件下恒成立即可），最终可以写成一下柿子：

$ 0 \le 2a_i \lt b_i $：

\[f(y)_i = \left\{ \begin{array}{ll} b_i - a_i &\quad y \in (-\infty, 2a_i] \cup [2b_i - 2a_i, +\infty) \\ -y + a_i + b_i &\quad y \in (2a_i, b_i) \\ y + a_i - b_i &\quad y \in [b_i, 2b_i - 2a_i) \end{array} \right. \]

然后在 $ b_i \lt2a_i \le 0 $ 同理可以推出：

$ b_i \lt2a_i \le 0 $：

\[f(y)_i = \left\{ \begin{array}{ll} a_i - b_i &\quad y \in (-\infty, 2b_i - 2a_i] \cup [2a_i, +\infty) \\ -y - a_i + b_i &\quad y \in (2b_i - 2a_i, b_i) \\ y - a_i - b_i &\quad y \in [b_i, 2a_i) \end{array} \right. \]

剩下的两个区间也同理推导一下即可：

$ a_i \lt 0 \lt b_i $：

\[f(y)_i = \left\{ \begin{array}{ll} b_i - a_i &\quad y \in (-\infty, 0] \cup [2b_i, +\infty) \\ -y - a_i + b_i &\quad y \in (0, b_i) \\ y - a_i - b_i &\quad y \in [b_i, 2b_i) \end{array} \right. \]

$ b_i \lt 0 \lt a_i $：

\[f(y)_i = \left\{ \begin{array}{ll} a_i - b_i &\quad y \in (-\infty, 2b_i] \cup [0, +\infty) \\ -y + a_i + b_i &\quad y \in (2b_i, b_i) \\ y + a_i - b_i &\quad y \in [b_i, 0) \end{array} \right. \]

现在我们也就能确定下来每一条 $ f(y)_i $ 的形状了，都是类似下图的形状，只是 “转折点” 不同，和 $ y $ 无关的认为其没有转折点即可。

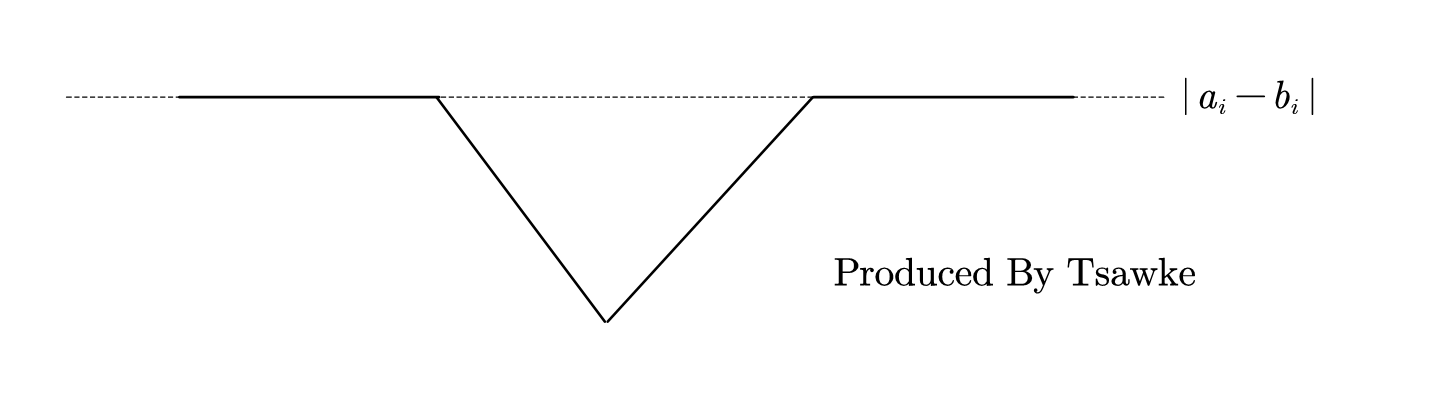
此时我们就需要考虑一下求 $ \sum_{i = 1}^nf(y)_i $ 了。

不难想到 $ O(n) $ 记录一下每一条线的 “转折点” 的位置，建立一个差分数组，然后每条线段斜率变为 $ -1 $ 之后对应位置加上 $ -1 $，斜率变为 $ 1 $ 之后加上 $ 2 $，变回与 $ y $ 相关之后再加上 $ -1 $，然后我们把差分数组做个前缀和，这样当前的前缀和数组的值就是 $ i $ 相对 $ i - 1 $ 的总答案变化量，对于 $ 0 $ 处我们认为其为 $ \sum_{i = 1}^n \vert a_i - b_i \vert $，然后在前缀和上再做一个前缀和，令其为 $ sum_i $，则不难想到答案即为 $ \min{sum_i} $，然后这里因为坐标值域范围很大，所以考虑离散化，为了写着方便，直接开一个 map 存即可，排序也省了。

至此，我们就做完了这道奇怪的大分类讨论，复杂度 $ O(n \log n) $，卡在排序上。

Code

#define _USE_MATH_DEFINES
#include <bits/extc++.h>

#define PI M_PI
#define E M_E
#define npt nullptr
#define SON i->to
#define OPNEW void* operator new(size_t)
#define ROPNEW(arr) void* Edge::operator new(size_t){static Edge* P = arr; return P++;}

using namespace std;
using namespace __gnu_pbds;

mt19937 rnd(random_device{}());
int rndd(int l, int r){return rnd() % (r - l + 1) + l;}
bool rnddd(int x){return rndd(1, 100) <= x;}

typedef unsigned int uint;
typedef unsigned long long unll;
typedef long long ll;
typedef long double ld;

template< typename T = int >
inline T read(void);

int N;
ll origin(0);
ll mn(LONG_LONG_MAX);
map < ll, ll > mp;
ll sum[310000]; int cnt(0);

void Insert(int p, int v){
    if(mp.find(p) == mp.end())mp.insert({p, v});
    else mp[p] += v;
}
void InsertAll(int sp1, int sp2, int sp3){
    Insert(sp1, -1);
    Insert(sp2, 2);
    Insert(sp3, -1);
}

int main(){
    N = read();
    for(int i = 1; i <= N; ++i){
        int a = read(), b = read();
        origin += abs(a - b);
        if(0 <= 2 * a && 2 * a < b)InsertAll(2 * a, b, 2 * b - 2 * a);
        else if(b < 2 * a && 2 * a <= 0)InsertAll(2 * b - 2 * a, b, 2 * a);
        else if(a < 0 && 0 < b)InsertAll(0, b, 2 * b);
        else if(b < 0 && 0 < a)InsertAll(2 * b, b, 0);
    }
    ll cur(0), sum(origin); int lft(INT_MIN);
    mn = origin;
    for(auto v : mp){
        sum += (ll)cur * (v.first - lft);
        cur += v.second, lft = v.first;
        mn = min(mn, sum);
    }
    printf("%lld\n", mn);
    fprintf(stderr, "Time: %.6lf\n", (double)clock() / CLOCKS_PER_SEC);
    return 0;
}

template < typename T >
inline T read(void){
    T ret(0);
    short flag(1);
    char c = getchar();
    while(c != '-' && !isdigit(c))c = getchar();
    if(c == '-')flag = -1, c = getchar();
    while(isdigit(c)){
        ret *= 10;
        ret += int(c - '0');
        c = getchar();
    }
    ret *= flag;
    return ret;
}

UPD

update-2022_11_07 初稿

标签：LG,le,vert,int,题解,Teleportation,lt,2a,quad
From： https://www.cnblogs.com/tsawke/p/16945600.html