拓扑排序学习笔记

标签：队列 cur int 拓扑笔记 AOV 序列排序

前言

在学习这篇文章之前，你需要了解的算法有：

基本图论知识
链式前向星（图的一种存储方式）
了解队列、栈等简单数据结构的实现，用 STL 也行。

什么是拓扑排序

AOV网的定义

在了解拓扑排序（topo sort）之前，我们还得了解一个东西：AOV 网。

AOV 网（Activity On Vertex）主要用于表示活动间的优先关系。

看下面一个 ~~非常不~~ 生动的例子。

假设你在玩游戏，你想要解锁一个宝箱。

想要解锁这个宝箱，你需要先完成一堆任务，而每个任务又需要先完成子任务后才能解锁。

具体如下：

那么 AOV 网长啥样呢？

先观察这个 AOV 网，自己寻找规律。

现在，请思考一下 AOV 网是如何创建的。

（思考ing）

思考完了吧，其实规律是很好找的，就一句。

如果 \(x \to y\)，说明完成任务 \(y\) 之前要先完成任务 \(x\)。

比如，想完成 \(4\)，必须先完成 \(1\) 与 \(6\)。

看一下图，\(6\) 与 \(1\) 是不是的确有一条边连向 \(4\) 呢？

进一步讲：

如果存在一条路径使得 \(x\) 通向 \(y\)，则完成任务 \(y\) 之前要先完成任务 \(x\)。

不过这一条件并没有太多作用。

以上就是 AOV 网大致的规律了，需要注意的是：

如果图上存在环，必定没有办法完成全部任务。
即，AOV 网必为一个 DAG（Directed Acycline Graph，有向无环图）。

拓扑排序的定义

说了这么一大坨，终于可以开始讲拓扑排序是神马东西了。

其实这东西特别简单，就是求一个序列，满足：

按照序列的顺序完成任务，可以将全部任务完成。

需要注意的是：

拓扑序列应该为 \(1\) 到 \(n\) 的其中一个全排列。
如果图上存在环，将没有拓扑序列（这一点前文提到过）。
拓扑序列一般有多个，但是程序通常只能求其中一个。

而拓扑排序，就是求出这个拓扑序列的。

下面，我们正式讲解拓扑排序的实现。

思路实现

1

用链式前向星存储这个图，并顺手计算每个点的入度。

不作解释，很简单。

int head[N], cur;
struct Node
{
	int now, nxt;
}e[M];
void add(int x, int y)
{
	e[++cur].now = y;
	e[cur].nxt = head[x];
	head[x] = cur;
}
int in[N]; //入度

scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++)
{
    int x, y;
    scanf("%d%d", &x, &y);
    add(x, y); //x->y
    in[y]++;
}

2

准备一个队列，并将所有入度为 \(0\) 的点压入队列。

代码：

int cur = 0;
queue <int> Q;
for (int i = 1; i <= n; i++)
    if (in[i] == 0)
        Q.push(i);

3

每次都将队首计入 topo[] 数组中。

然后遍历所有队首点可以一次到达的点，如 \(1\) 要遍历到 \(2\)、\(3\)、\(4\)。

（正是因为这一点，我们采用链式前向星）

然后将遍历到的点 in[x]--。

若当前点入度被减成 \(0\) 了，说明这个任务可以执行了，即：将当前点压入队列。

一直执行，直到队列为空。

代码：

int topo[N];

while (!Q.empty())
{
    int x = Q.front(); //截取队首
    Q.pop(); //弹出
    topo[++cur] = x;  //扔进拓扑序列中
    for (int i = head[x]; i; i = e[i].nxt)
    {
        int t = e[i].now; //易错，是 e[i].now 而非 i
        in[t]--;
        if (in[t] == 0) Q.push(t);
    }
}

4

最后，我们要判断是否存在拓扑序列。

很简单，不存在拓扑序列，当且仅当 \(\text{拓扑序列元素个数} < n\)。

为什么呢？

看这张图，显然是一个普通的环。

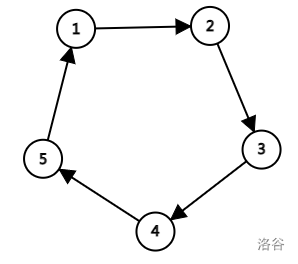
所有点入度都不为 \(0\)，故不存在拓扑序列。

那如果外面还有一些点呢？

此处的点 \(a\)、\(b\)、\(c\)、\(d\) 之外可能还有其他点。

假设点 \(a\)、\(b\)、\(c\)、\(d\) 已经入队了。

你会发现，点 \(a\)、\(b\)、\(c\)、\(d\) 仅仅能处理当前的边，所以最后仍然会留下这个环。

综上所述，可以轻松判断拓扑序列是否符合要求。

代码：

if (cur < n) printf("This graph isn't a DAG."); //图存在环
else
{
    for (int i = 1; i <= n; i++) printf("%d ", topo[i]);
}

总代码

完整代码

#include <iostream>
#include <cstdio>
#include <queue>
#define N 233
#define M 2005
using namespace std;
int head[N], cur;
struct Node
{
	int now, nxt;
}e[M];
void add(int x, int y)
{
	e[++cur].now = y;
	e[cur].nxt = head[x];
	head[x] = cur;
}
int n, m;
int in[N]; //入度
int topo[N];
bool topo_sort()
{
	cur = 0; //再次利用 
	queue <int> Q;
	for (int i = 1; i <= n; i++)
		if (in[i] == 0)
			Q.push(i);
	while (!Q.empty())
	{
		int x = Q.front();
		Q.pop();
		topo[++cur] = x;
		for (int i = head[x]; i; i = e[i].nxt)
		{
			int t = e[i].now;
			in[t]--;
			if (in[t] == 0) Q.push(t);
		}
	}
	return (cur == n);
}
int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= m; i++)
	{
		int x, y;
		scanf("%d%d", &x, &y);
		add(x, y); //x->y
		in[y]++;
	}
	bool chk = topo_sort();
	if (chk == false) printf("This graph isn't a DAG."); //图存在环
	else
	{
		for (int i = 1; i <= n; i++) printf("%d ", topo[i]);
	}
    return 0;
}

测试样例：

有关『队列』的思考

其实，此处必须用队列吗？

了解了拓扑排序的原理后，很容易发现，不一定用队列。

比如，可以使用栈。

观察一下两种数据结构的不同答案。

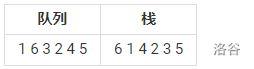
很明显，两种序列都是对的，因为前文提到过，拓扑序列并非唯一。

不过，两个序列并没有什么明显的规律呀！

有些题目会让你求：

一行，输出拓扑序列。

如果不存在拓扑序列，输出 \(-1\)。

如果有多个拓扑序列，输出字典序最小的那一个。

此时，你想到了什么？

没错！优先队列！

如果我们使用优先队列，就可以让拓扑序列相对有序了。

我们再列一个表格。

是不是稍微有一点规律了？！

此外，如果你给优先队列重载，就可以达到不同的需求了。

如果你重载成随机 true false，你就可以得到多个不同的拓扑序列了！

结语 & 参考文献

拓扑排序其实挺简单的，对吧！

参考了《算法训练营海量题解+竞赛刷题：入门篇》一书，样例参照了此书。

本文的图均为作者所制，未经允许不可转载。图使用 https://csacademy.com/app/graph_editor/ 绘画。

前台所有表格都炸了，只好在后台截图。

今后会在本文加入例题的！

首发：2022-05-15 22:06:31

标签：队列,cur,int,拓扑,笔记,AOV,序列,排序
From： https://www.cnblogs.com/liangbowen/p/16622862.html

前言