泛函
泛函定义
对于某一类函数集合\(\{x(t)\}\) 中的每一个函数 \(x(t)\), 在映射关系 \(J\) 下均有一个确定的数与之对应,则称 \(J\) 为依赖于函数 \(x(t)\) 的泛函,记作$$J=J[x(.)]=J[x(t)]$$
注:泛函与函数的区别
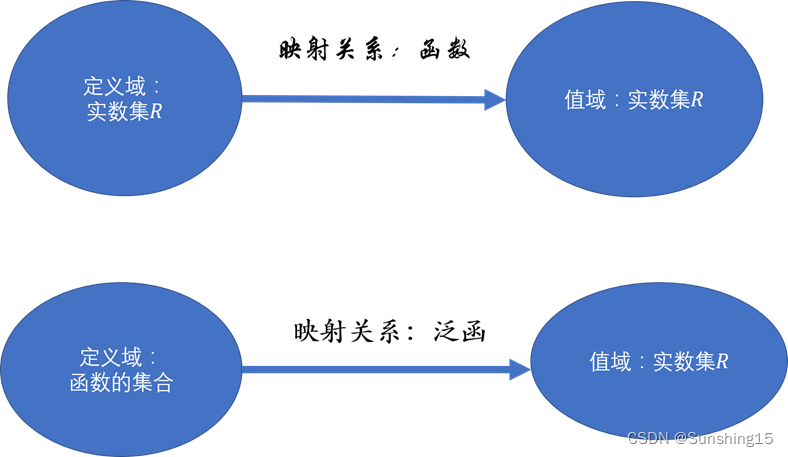
泛函即为以函数为自变量的一种映射到实数域的映射关系。而函数则是以某一实数为自变量映射到实数域的映射关系。这里的\(J[x(t)]\)可理解为整条曲线 \(x(t)\) 在映射关系 \(J\) 下对应一个实数值。
泛函的变分
自变量的变分
泛函 \(J[x(t)]\) 的自变量函数 \(x(t)\) 与标称函数 \(x^*(t)\) 之间的差值函数$$\delta x(t)=x(t)-x^*(t)$$ 称为泛函自变量的变分。
泛函相近
- 零阶相近
当泛函自变量的变分 \(\delta x(t)\) 的绝对值对于 \(x(t)\) 定义域中的一切 \(t\) 都很小时,称函数 \(x(t)\) 与 \(x^*(t)\) 是接近的,也称为零阶相近。 - 一阶相近
当泛函自变量的变分 \(\delta x(t)\) 的绝对值以及 \(\delta x(t)\) 的一阶导数的绝对值对于 \(x(t)\) 定义域中的一切 \(t\) 都很小,则称函数 \(x(t)\) 与 \(x^*(t)\) 是一阶相近的。 - K阶相近
当 \(|x(t)-x^*(t)|\), \(|\dot{x}(t)-\dot{x}^*(t)|\), \(\ldots\), \(|x^{(k)}(t)-x^{*(k)}(t)|\) 对一切 \(t\) 都很小时, 称函数 \(x(t)\) 与 \(x^*(t)\) 是 \(k\) 阶相近的。
泛函距离
- 零阶距离
在连续函数全体组成的函数空间 \(C[a,b]\)中,泛函自变量的距离可定义为$$d[x(t),x^(t)]=\displaystyle \max_{a\leq t\leq b}{x(t)-x^(t)}$$ - \(k\) 阶距离
由在区间\([a,b]\)上连续且具有连续的 \(k\) 阶导数的函数的全体构成的函数空间 \(C^{k}[a,b]\) 中,任意两个函数间的\(k\)阶距离定义为
泛函的连续性
对于任意给定的正数 \(\varepsilon\), 总可以找到一个正数 \(\delta\), 使得当 \(d(x, x^*)<\delta\) 时, 有
\[|J[x(t)]-J[x^*(t)]|<\varepsilon \]则称泛函 \(J[x(t)]\) 在 \(x^*(t)\) 处是连续的。其中, \(d(x, x^*)=\displaystyle \max_{a\leq t \leq b}|x(t)-x^*(t)|\)。根据所采用的泛函自变量之间的距离的定义方式的不同,可分别定义泛函的零阶连续以及 \(k\) 阶连续泛函。
Lemma 1: 如果函数 \(F(t)\) 在区间 \([t_0, t_f]\) 上是连续的, 而且对于只满足某些一般条件的任意选定的函数 \(\eta(t)\) 有 \(\displaystyle\int_{t_0}^{t_f}F(t)\eta(t)dt=0\), 则在区间 \([t_0, t_f]\) 上有 \(F(t)=0\)。
线性泛函
连续泛函 \(J[x(t)]\) 如果满足如下两个条件:$$J[x_1(t)+x_2(t)]=J[x_1(t)]+J[x_2(t)]$$$$J[Cx(t)]=CJ[x(t)]$$其中 \(C\) 为常数, 则 \(J[x(t)]\) 为线性泛函。
泛函的变分
- 宗量:若函数 \(x(t)\) 是映射关系 \(J\) 的自变量函数,则称 \(x(t)\) 为泛函 \(J[x(t)]\) 的宗量函数。
- 宗量的变分:宗量的变分是指在同一函数类中的两个宗量函数间的差,即:$$\delta x(t)=x(t)-x^*(t).$$
- 泛函的增量
由自变量函数 \(x(t)\) 的变分 \(\delta x(t)\) 引起泛函 \(J[x(t)]\) 的增量
为泛函 \(J[x(t)]\) 的增量。
- 泛函的变分
当宗量函数 \(x(t)\) 有变分时,泛函 \(J[x(t)]\) 的增量 \(\Delta J[x(t)]\) 可表示为
其中\(\Delta J\) 的线性部分称为泛函的变分,记作 \(\delta J\),即 $$\delta J=\frac{dJ}{dx}|_{x^*}\delta x,$$换句话说即为泛函的变分是泛函增量的线性主部。
Lemma 2: 泛函的变分 \(\delta J=\frac{\partial}{\partial \alpha}J[x(t)+\alpha \delta x(t)]|_{\alpha=0}\)
Example 1: 计算泛函 \(J=\displaystyle \int_0^1x^2(t)dt\) 的变分。
\[\begin{aligned} \delta J&=\frac{\partial}{\partial \alpha}J[x(t)+\alpha\delta x(t)]|_{\alpha=0}\\ &=\frac{\partial}{\partial \alpha}\displaystyle\int_0^1[x(t)+\alpha\delta x(t)]^2dt|_{\alpha=0}\\ &=\displaystyle\int_0^12[x(t)+\alpha \delta x(t)]\delta x(t)dt|_{\alpha=0}\\ &=\displaystyle\int_0^12x(t)\delta x(t)dt \end{aligned}\]泛函的极值
泛函极值的定义
如果泛函 \(J[x(t)]\) 在 \(x(t)=x^*(t)\) 的邻域内,其增量
\[\Delta J=J[x(t)-x^*(t)]=J[x(t)]-J[x^*(t)]\geq 0 \]或
\[\Delta J=J[x(t)-x^*(t)]=J[x(t)]-J[x^*(t)]\leq 0 \]则称泛函 \(J[x(t)]\) 在 \(x(t)=x^*(t)\) 有极小值或极大值。
泛函的极值
- 强极值:如果 \(J[x^*(t)]\) 是在与 \(x(t)\) 仅仅具有零阶接近度的曲线 \(x(t)\) 的泛函中比较得出的极值,称为强极值。
- 弱极值:如果 \(J[x^*(t)]\) 是在与 \(x(t)\) 具有一阶或一阶以上接近度的曲线 \(x(t)\) 的泛函中比较得出的极值,称为弱极值。
泛函极值条件
- 必要条件
若可微泛函 \(J[x(t)]\) 在曲线 \(x(t)=x^*(t)\) 达到极值,则泛函 \(J[x(t)]\) 在 \(x(t)=x^*(t)\) 上的变分等于零,即 \(\delta J[x^*(t)]=0\)。
证明:对于任意给定的 \(\delta x(t)\) 来说, \(J[x^*(t)+\alpha \delta x(t)]\) 是实变量 \(\alpha\) 的函数。泛函 \(J[x(t)]\) 在 \(x^*(t)\) 达到极值,即函数 \(J[x^*(t)+\alpha \delta x(t)]\) 在 \(\alpha=0\) 时达到极值,所以它的导数在 \(\alpha=0\) 时应为零,即$$\frac{\partial}{\partial\alpha}J[x^*(t)+\alpha\delta x(t)]|_{\alpha=0}=0$$ 由变分引理可知 \(\frac{\partial}{\partial\alpha}J[x^*(t)+\alpha\delta x(t)]|_{\alpha=0}=\delta J[x^*(t)]=0\)。得证。 - 充要条件
设可微泛函 \(J(x)\) 存在二次变分, 则在 \(x=x^*\) 处达到极小值的充要条件为:
同理,设可微泛函 \(J(x)\) 存在二次变分,则在 \(x=x^*\) 处存在极大值的充要条件为:
\[\delta J(x^*)=0,\delta^2J(x^*)<0. \] 标签:函数,变分,泛函,----,delta,alpha,极值,最优控制 From: https://www.cnblogs.com/sunshining15/p/16918752.html