前言:本人已做完网络流24题。
0. 基础:
Dinic最大流/最小割:https://www.luogu.com.cn/blog/creationhy/dinic
Dinic费用流:https://www.luogu.com.cn/blog/creationhy/dinic-fei-yong-liu-post
正经人谁用HLPP。Dinic太强大了。
1. 相同分组增加贡献:
例题P1361 P1646。
先Dinic计算最小割,总和-最小割即为答案。
连边:
s→i[1,n],边权为i在第一组的贡献。
i[1,n]→t,边权为i在第二组的贡献。
如果第j个输入表示点集$S$都在第一组时会额外增加k的回报,连边:
s→j,边权为k;
j→$S$,边权为inf;
否则(如果在第二组):
j→t,边权为k;
$S$→j,边权为inf;
答案即为总边权(除去inf)减最小割。
P1361样例:
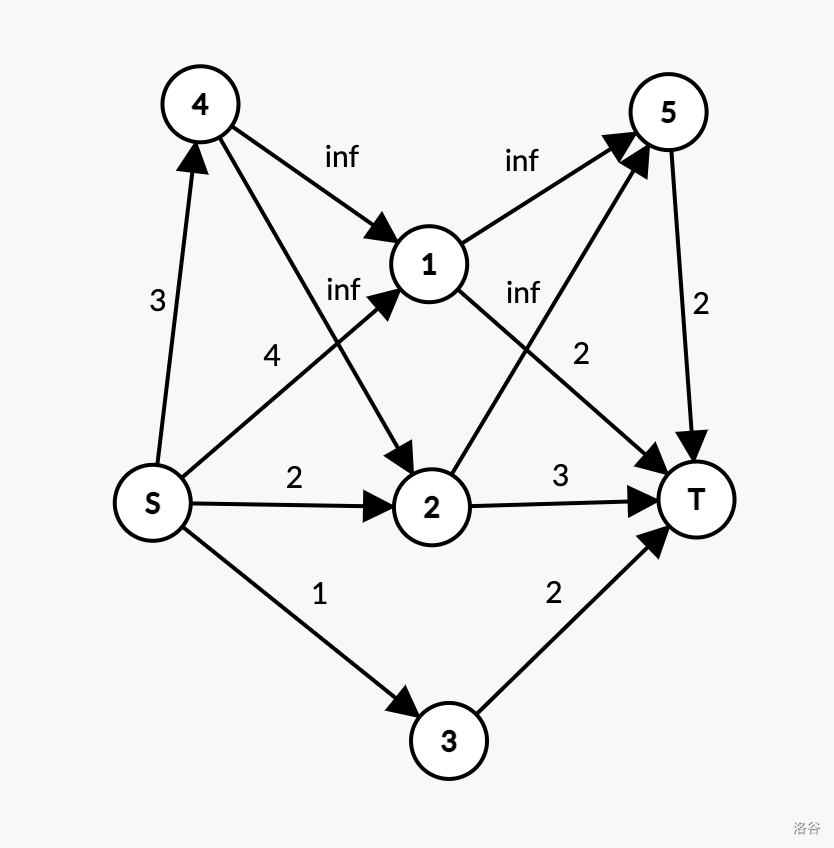
2. 共用消耗,完成增加贡献:
例题P2762 P4174。
分层连边:
对于每个任务i,设需要的工具集为$S$,做完可以获得k的回报:
s→i,边权为k;
i→$S$,对于$S$的每个点,边权为inf。
对于每个工具i:
i→t,边权为i的花费。
答案即为每个任务回报和减最小割。
P2762样例:
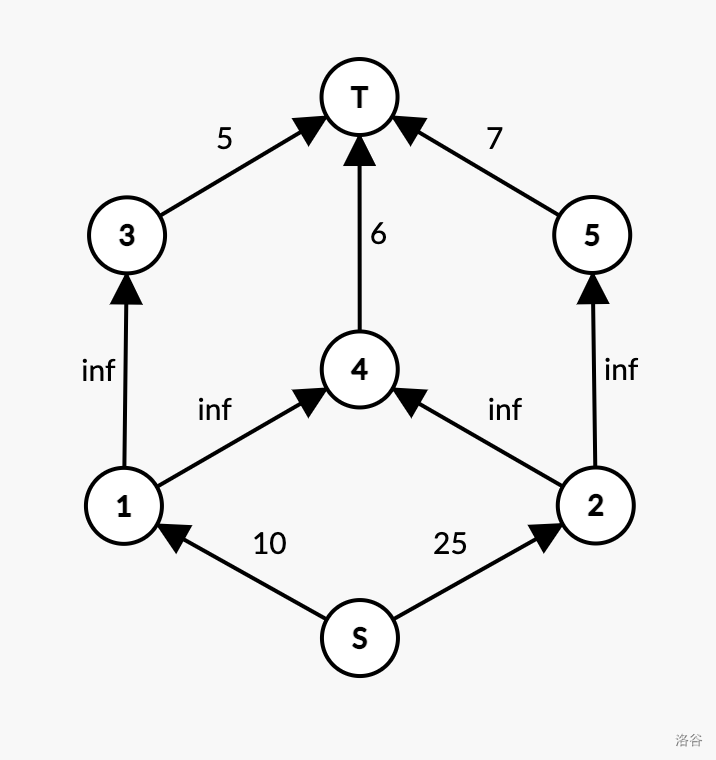
3. 棋盘选点问题:
例题P2774 P3355。
将点分为两组(直接用(x+y)&1分类即可)。
对于第一组点集$S$,连边$S$→t,边权为所求结果。
对于另外一组$S$,连边s→$S$,边权为所求结果;对于每个点u,连边u→$V$,$V$为和u相邻的点集,边权inf。
答案依旧为总和减最小割。
P2774样例:
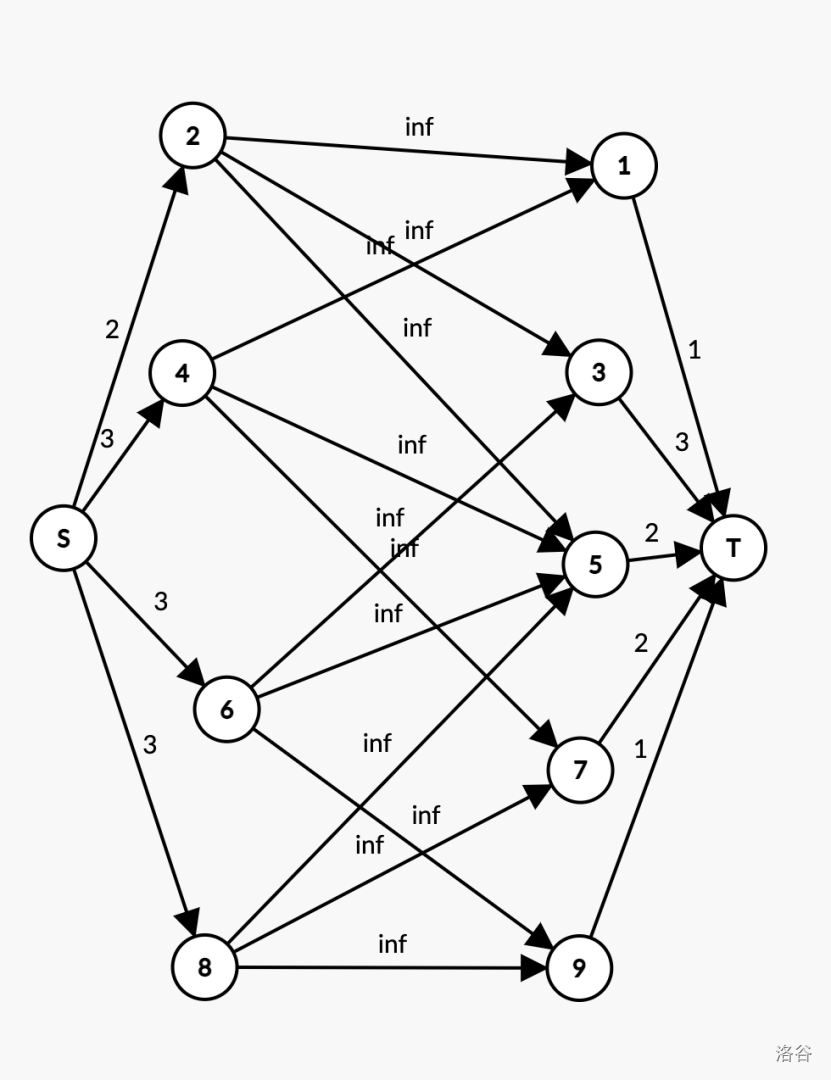
4. 分配问题 Basic
例题P4014 P4015。(P2763 P3254等其实也差不多)
连边:
s→i[1,n],流量1,费用0,表示每个人。
i[n+1,n*2]→t,流量1,费用0,表示每个任务。
i[1,n]->j[n+1,n*2],流量1,费用$c_{i,j}$。
其中P4014第二问还要求跑最大费用最大流,费用建负数即可。
边太多了,图就不放了。
5. 分配问题 Plus
例题P2053 P2050。(P2050稍难,要求动态加点)
其实就是模型4的升级版,将模型4里面每个人拆成m个人,即第i个人拆成第j时段的第i人即可。
6. 重新建图/残量网络
例题P4013 P4014 P4015。
如果一题有很多问,而一问又可以转化为上一问的图+某些新的边(比如P4013第二问就是第一问再加上任意两点连边inf),那么就会涉及到这个。
如果是最大流(有这种题,但是我忘了),跑完Dinic后把答案存起来,在残量网络上建新的边,再跑一遍,两次答案之和即为第二次的流量。
但如果是费用流,就要重新建图了。P4013 P4014都是重新建图的例子。跑完后把链式前向星的head数组、链式前向星的tot、MaxFlow值、MinCost/MaxCost值全部初始化,再建图即可。
7. 上下界网络流
7.1. 上下界最大流
懒得画图了。放代码吧。
1 int s1 = n + m + 1, t1 = n + m + 2, s2 = n + m + 3, t2 = n + m + 4;
2 s = s2, t = t2;
3 for (int i = 1; i <= m; i++)
4 {
5 ll x;
6 cin >> x;
7 in[t1] += x;
8 out[n + i] += x;
9 add(n + i, t1, inf - x);
10 }
11 for (int i = 1; i <= n; i++)
12 {
13 ll x, y, T, l, r;
14 cin >> x >> y;
15 add(s1, i, y);
16 for (int j = 1; j <= x; j++)
17 {
18 cin >> T >> l >> r;
19 T++;
20 in[n + T] += l;
21 out[i] += l;
22 add(i, n + T, r - l);
23 }
24 }
25 ll maxFlow = 0;
26 for (int i = 1; i <= n + m + 2; i++)
27 if (in[i] > out[i])
28 add(s, i, in[i] - out[i]), maxFlow += in[i] - out[i];
29 else
30 add(i, t, out[i] - in[i]);
31 add(t1, s1, inf);
32 if (Dinic() != maxFlow)
33 {
34 cout << -1;
35 return 0;
36 }
37 int ans = val[tot - 1];
38 val[tot - 1] = val[tot - 2] = 0;
39 s = s1, t = t1;
40 cout << ans + Dinic() << "\n\n";
inf. 写在最后
网络流24题里确实还有一些经典建模本文没有涉及到。因为本人很懒。拜拜。
标签:连边,边权,网络,笔记,学习,add,inf,例题,out From: https://www.cnblogs.com/creation-hy/p/16915904.html