SA
今天翻出了很久之前给自己安排做的题
P4035 [JSOI2008]球形空间产生器
结果我把高斯消元忘了,想起之前拿随机化贪心骗分的快乐,于是学习了另一种解法A掉这道题。
看标签都知道,模拟退火
我打的第一个模拟退火没用随机化,珂以算作爬山。
首先,我们为了尽可能的得到最快最优的答案。先把初始状态设为每一维度的平均值。
以二维圆形为例子(样例):
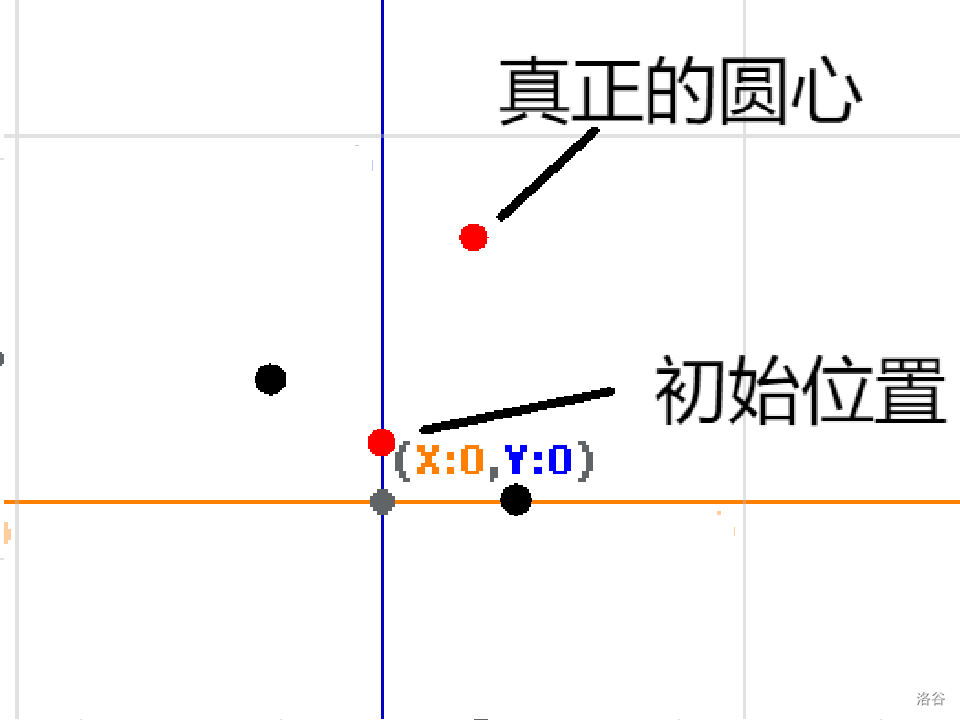
我们找到当前状态与每个点的距离平均值。若小于这个平均值则往远离该点的方向移动,反之靠近该点。
具体移动多少,枚举每一维,然后把该维答案与该点的差乘以平均值与距离之差与平均值的比值。
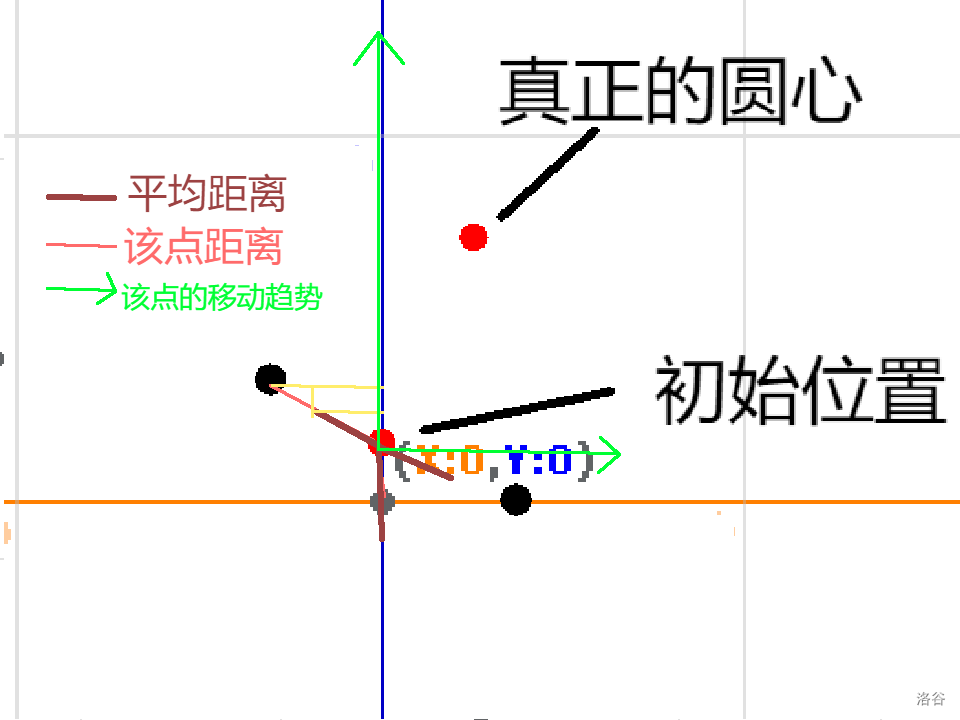
这部分的代码是:
for(int i=1;i<=n+1;i++)
for(int j=1;j<=n;j++)
cha.x[j]+=((dis[i]-ave))*(a[i].x[j]-ans.x[j])/ave;cha就是每一维的改变值
最后根据模拟退火的温度变化,把温度设为一个系数,乘以差值在加上当前状态,累加后的当前状态经过降温后又将重复操作,直到温度达到最低温度。
这是累加代码
for(int i=1;i<=n;i++)ans.x[i]+=cha.x[i]*t;这是模拟退火的关键(温度变化):
for(double t=10000;t>0.0001;t*=0.99996)sa(t);最后,我们用玄学做法AC了这道省选紫题。
下面我们再看一道SA的模板题 P1337 [JSOI2004] 平衡点 / 吊打XXX
前置知识:力的合成与分解。
若不知道力的合成与分解,计算合力可用一下代码。
double energy(double x,double y){
double ans=0;
for(int i=1;i<=n;i++)ans+=dist(x,y,a[i].x,a[i].y)*a[i].w;
return ans;
}意思就是把这个点拨到x,y位置,若增加一个外力卡住正好可以平衡,这个外力就珂以用这个函数计算。
我们的目的就是找到一个值使得这个合力尽可能小。有两种办法。
第一个是两次三分法找到二元单峰函数的最小值,这里不再展开介绍。
第二种就是模拟退火。
其实还有计算几何的做法我不会(doge)。
我们在目前的x,y上各增加一个随机值,然后对比energy的大小比较。
如果小于energy或者差值可以被接受,则把答案设为随机增加后的新答案。
同时降温,使得x,y的变化趋势减弱。
这里给出核心代码
double sa(){
for(double t=1145;t>eps;t*=0.999){
double tx=ansx+(rand()*2-fi)*t,ty=ansy+(rand()*2-fi)*t;
double del=energy(tx,ty)-energy(ansx,ansy);
if(del<0)ansx=tx,ansy=ty;
else if(exp(-del/t)*fi>rand())ansx=tx,ansy=ty;
}
}随机化
P2210 Haywire,这题珂以算是随机化的模板题
每个牛有三个朋友,可以随机排列牛。( N≤12N≤12 )
你是不是想全排列爆搜?
然鹅 12!≈4\times10^812!≈4×108 时间是不优秀的。
于是我们可以随机化贪心。
随机构造一个奶牛的顺序,然后模拟铁路的长度即可,因为是来回的,所以答案要除以2。
这时候一次贪心的代码:
void solve(){
random_shuffle(p+1,p+n+1);
for(int i=1;i<=n;i++)id[p[i]]=i;
int res=0;
for(int i=1;i<=n;i++){
int now=id[f[i].zj],a=id[f[i].a],b=id[f[i].b],c=id[f[i].c];
res+=abs(now-a)+abs(now-b)+abs(now-c);
}
ans=min(ans,res);
}我粗略试了一下,随机化 10^6106 次即可AC,远远优于 4\times10^84×108
在结尾,我送上一道好题
完结撒花
标签:int,double,energy,笔记,随机化,模拟退火,SA From: https://www.cnblogs.com/masida-hall-LZ/p/16623817.html