记录一下爆炸的模拟赛。
T1
原题,这道题的题解之前写过,在这。
T2
由于边数接近点数,整个图的形态接近树,想到建出原图的一个生成树(任意一个),这样两个点的距离分为两类:
- 只经过树边。
- 经过非树边。
对于第一种,直接维护树的深度就行。
对于第二种,考虑枚举非树边的点i,答案就为 \(\min dis_{u,i}+dis_{i,v}\),非树边只有 \(21\) 条,点就只有 \(42\) 个,暴力以每个点跑 dijsktra 就行了。
T3
由于 \(d\) 在 \(\sqrt{\min(n,m)}\) 以内,考虑枚举 \(d\)。
记 \(S(d)\) 为多少对 \(i,j\) 满足答案是 \(d\)。
\(i,j\) 都有因子 \(d^2\),那么 \(i,j\) 的另一个因子一定在 \(1\sim \lfloor \frac{n}{d}\rfloor\) 和 \(1\sim \lfloor \frac{m}{d}\rfloor\),一共 \(\lfloor \frac{n}{d}\rfloor\lfloor \frac{m}{d}\rfloor\) 种情况,但随意选可能让答案变大,但变大后一定是 \(d\) 的倍数,因此减去 \(d\) 的倍数的 \(S\) 就行了。
具体地:
由调和级数可知复杂度为 \(\mathcal{O}(\sqrt{n}\log \sqrt{n})\)。
T4
记 \(a_i\) 为 \(i\) 处的石子数,\(A\) 为先手,\(B\) 为后手。
对于博弈类问题先考虑最简单的情况。
当只有两个点的时候

当盒子在 \(1\) 号点,\(A\) 只能移向 \(2\),\(B\) 只能由 \(2\) 移向 \(1\),那么 \(A\) 获胜的条件就是 \(a_1>a_2\)。
现在考虑更复杂的情况
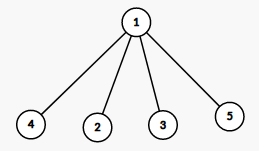
假设盒子在 \(1\),那么 \(A\) 一定会选择移向某个儿子,然后 \(B\) 只能又挪回 \(1\),那么 \(A\) 一定会移向儿子中石子最少的,获胜条件是 \(\min a_v<a_i\)。
现在考虑一般情况
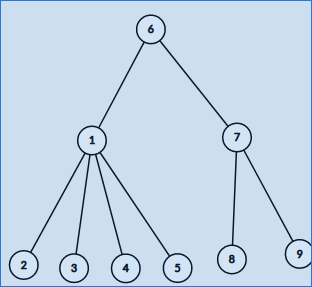
假设盒子在 \(6\)。
如果 \(1\) 号点对应子树为先手必胜,那么 \(A\) 一定不会移向 \(1\),因为 \(B\) 一定会把盒子移进子树发展下去。反之,如果 \(1\) 是先手必败,那么 \(A\) 移向 \(1\) 后,\(B\) 一定是把盒子移回 \(6\),不然进入 \(1\) 子树后 \(B\) 必败。
因此最后仍然会像情况 \(2\) 一样“反复横跳”,因此 \(A\) 的获胜条件为所有状态为“先手必败”子节点中 \(a\) 的最小值小于 \(a_i\)。