算法1.三次线性扫描\(O(n)\)
-
观察整个图形,考虑对水的面积按 列 进行拆解
-
注意到,每个矩形条上方所能接受的水的高度,是由它左边
最高的矩形,和右边最高的矩形决定的。 -
具体地,假设第 i 个矩形条的高度为
height[i],且矩形条左边 最高的 矩形条的高度为left_max[i],右边 最高的 矩形条高度为right_max[i],则该矩形条上方能接受水的高度为min(left_max[i], right_max[i]) - height[i]。 -
分别从左向右扫描求 left_max,从右向左求 right_max,最后统计答案即可。
注意特判 n 为 0。
时间复杂度
三次线性扫描,故只需要 O(n) 的时间。
空间复杂度
需要额外 O(n) 的空间记录每个位置左边最高的高度和右边最高的高度。
代码
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size();
vector<int> left_max(n), right_max(n);
left_max[0] = height[0];
for(int i = 1; i < n; i++)
left_max[i] = max(left_max[i - 1], height[i]);
right_max[n - 1] = height[n - 1];
for(int i = n - 2; i >= 0; i--)
right_max[i] = max(right_max[i + 1], height[i]);
int ans = 0;
for(int i = 0; i < n; i++)
ans += min(left_max[i], right_max[i]) - height[i];
return ans;
}
};
算法2.单调栈
换一种思路,按行进行拆分
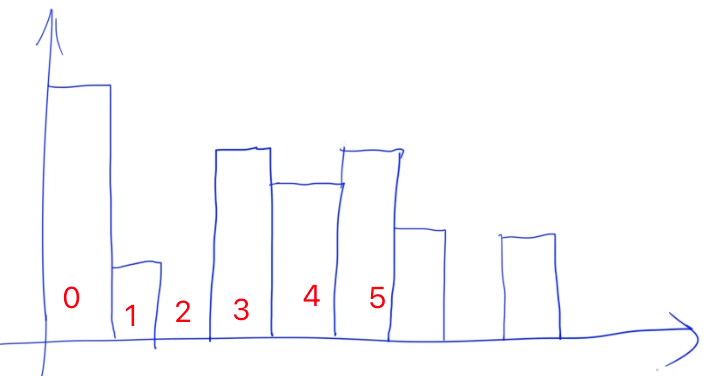
- 维护一个递减的单调栈
- 0 1 2都是递减的,即当前高度小于栈顶高度,所以入栈
- 当走到3时,3的高度比栈顶2的高度要高,所以要出栈计算
- 先将单调栈的栈顶2的弹出,然后加上1、2和3构成的水沟的高度
- 再将单调栈的栈顶1的弹出,加上0123构成的水沟高度
- 不断重复,直到栈顶高度高于3的高度,将3入栈
代码
class Solution {
public:
int trap(vector<int>& height) {
int n = height.size(), ans = 0, top = -1;
int stack[n];
for(int i = 0; i < n; i++)
{
while(top != -1 && height[stack[top]] <= height[i])
{
int buttom = stack[top--];
if(top == -1) break;
int l = stack[top];
ans += (min(height[i], height[l]) - height[buttom]) * (i - l - 1);
}
stack[++top] = i;
}
return ans;
}
};