题目链接
2935. 信用卡凸包
信用卡是一个矩形,唯四个角作了圆滑处理,使它们都是与矩形的两边相切的 \(\frac{1}{4}\) 圆,如下图所示。

现在平面上有一些规格相同的信用卡,试求其凸包的周长。
注意凸包未必是多边形,因为它可能包含若干段圆弧。
输入格式
第一行是一个正整数 \(n\),表示信用卡的张数。
第二行包含三个实数 \(a, b, r\),分别表示信用卡(圆滑处理前)竖直方向的长度、水平方向的长度,以及 \(\frac{1}{4}\) 圆的半径。
之后 \(n\) 行,每行包含三个实数 \(x, y, θ\),分别表示一张信用卡中心(即对角线交点)的横、纵坐标,以及绕中心逆时针旋转的弧度。
输出格式
输出只有一行,包含一个实数,表示凸包的周长,四舍五入精确到小数点后 \(2\) 位。
数据范围
\(1 \le n \le 10000\),
\(0.1 \le a,b \le 1000000.0\),
\(0.0 \le r < \min \{ a/4,b/4 \}\),
\(|x|,|y| \le 1000000.0\),
\(0 \le θ < 2 \pi\)
输入样例1:
2
6.0 2.0 0.0
0.0 0.0 0.0
2.0 -2.0 1.5707963268
输出样例1:
21.66
样例1解释

本样例中的 \(2\) 张信用卡的轮廓在上图中用实线标出,如果视 \(1.5707963268\) 为 \(\pi/2\)( \(\pi\) 为圆周率),则其凸包的周长为 \(16+4 \times \sqrt 2\)。
输入样例2:
3
6.0 6.0 1.0
4.0 4.0 0.0
0.0 8.0 0.0
0.0 0.0 0.0
输出样例2:
41.60
样例2解释

输入样例3:
3
6.0 6.0 1.0
4.0 4.0 0.1745329252
0.0 8.0 0.3490658504
0.0 0.0 0.5235987756
输出样例3:
41.63
样例3解释
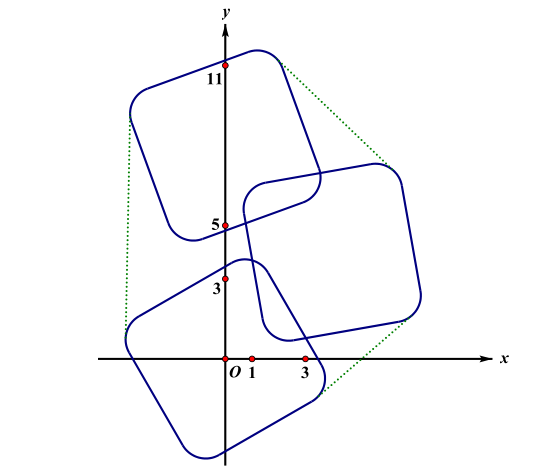
其凸包的周长约为 \(41.628267652\)。
解题思路
凸包
求解直线比较容易,即将所有圆心求一遍凸包,但计算弧线部分的周长比较困难,考虑将最后的凸包想象成一个 \(n\) 边形,\(n\) 边形的每个内角 \(\alpha_i\) 和对应弧线对应的弧角 \(beta_i\) 都有这样的关系 \(\alpha_i+\beta_i=\pi\),而由 \(n\) 边形内角和可知:\((n-2)\times \pi+\sum \beta_i=n\pi\),得 \(\sum \beta_i=2\pi\),即最后形成的弧线是一个圆
- 时间复杂度:\(O(nlogn)\)
代码
// Problem: 信用卡凸包
// Contest: AcWing
// URL: https://www.acwing.com/problem/content/2938/
// Memory Limit: 64 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
// %%%Skyqwq
#include <bits/stdc++.h>
//#define int long long
#define help {cin.tie(NULL); cout.tie(NULL);}
#define pb push_back
#define fi first
#define se second
#define mkp make_pair
using namespace std;
typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
template <typename T> bool chkMax(T &x, T y) { return (y > x) ? x = y, 1 : 0; }
template <typename T> bool chkMin(T &x, T y) { return (y < x) ? x = y, 1 : 0; }
template <typename T> void inline read(T &x) {
int f = 1; x = 0; char s = getchar();
while (s < '0' || s > '9') { if (s == '-') f = -1; s = getchar(); }
while (s <= '9' && s >= '0') x = x * 10 + (s ^ 48), s = getchar();
x *= f;
}
const int N=50005;
const double pi=acos(-1),eps=1e-8;
typedef pair<double,double> PDD;
int n,cnt,stk[N],top;
int dx[]={-1,-1,1,1},dy[]={-1,1,1,-1};
double a,b,r;
PDD q[N];
PDD operator-(PDD a,PDD b)
{
return {a.fi-b.fi,a.se-b.se};
}
PDD rotate(PDD a,double angle)
{
return {a.fi*cos(angle)+a.se*sin(angle),-a.fi*sin(angle)+a.se*cos(angle)};
}
int sign(double x)
{
if(fabs(x)<eps)return 0;
if(x<0)return -1;
return 1;
}
double cross(double x1,double y1,double x2,double y2)
{
return x1*y2-x2*y1;
}
double area(PDD a,PDD b,PDD c)
{
return cross(b.fi-a.fi,b.se-a.se,c.fi-a.fi,c.se-a.se);
}
double get_dist(PDD a,PDD b)
{
return sqrt((a.fi-b.fi)*(a.fi-b.fi)+(b.se-a.se)*(b.se-a.se));
}
void andrew()
{
sort(q+1,q+1+cnt);
for(int i=1;i<=cnt;i++)
{
while(top>=2&&sign(area(q[stk[top-1]],q[stk[top]],q[i]))<=0)top--;
stk[++top]=i;
}
int k=top;
for(int i=cnt;i>=1;i--)
{
while(top>k&&sign(area(q[stk[top-1]],q[stk[top]],q[i]))<=0)top--;
stk[++top]=i;
}
if(cnt>1)top--;
}
int main()
{
scanf("%d%lf%lf%lf",&n,&a,&b,&r);
a=a/2-r,b=b/2-r;
while(n--)
{
double x,y,z;
scanf("%lf%lf%lf",&x,&y,&z);
for(int i=0;i<4;i++)
{
PDD t=rotate({dx[i]*b,dy[i]*a},-z);
q[++cnt]={x+t.fi,y+t.se};
}
}
andrew();
double res=0;
for(int i=1;i<top;i++)res+=get_dist(q[stk[i]],q[stk[i+1]]);
res+=get_dist(q[stk[1]],q[stk[top]]);
printf("%.2lf",res+pi*r*2);
return 0;
}