笛卡尔树讲解

前言

笛卡尔树 算是比较基础的数据结构了，但需要 笛卡尔树 的题目较少，且很多 笛卡尔树 的题都可以用其他解法解决，所以这个算法并不算的上热门，然而就在前天晚上，CF1748E 这道题需要用到 笛卡尔树 解决，所以蒟蒻のyzh打算写一篇笛卡尔树的文章，来温故这个算法！

文章中部分图片使用了OIwiki的图片，如有侵权 私信删图

笛卡尔树の性质

定义二元组 \((k,w)\) 组成一棵树，其中 \(k\) 满足二叉搜索树性质，而 \(w\) 需要满足堆的性质（通常是小顶堆，具体根据题目要求）。

例如下图（图片来源：维基百科）

上图是笛卡尔树的一种:

二元组 \((k,w)\) ，对于一个序列 \(a_1,\cdots ,a_n\) ，\(k\) 为下标 \(i\)，\(w\) 为 \(a_i\)。

关于treapの小疑问？

读者看到这可能会认为，这不就treap吗？没错，笛卡尔树就是treap一种形态，只不过笛卡尔树插入时，\(k\) 值一定是单调的！ 所以下面的构建操作总复杂度为 \(O(n)\).

构建

过程

我们考虑将元素按照键值 \(k\) 排序。然后一个一个插入到当前的笛卡尔树中。

考虑如何满足笛卡尔树性质。

每次我们插入的元素必然在这个树的右链（右链：即从根结点一直往右子树走，经过的结点形成的链）的末端。从下往上比较右链结点与当前结点 \(u\) 的 \(w\)，如果找到了一个右链上的结点 \(x\) 满足 \(x_w<u_w\)，就把 \(u\) 接到 \(x\) 的右儿子上，而 \(x\) 原本的右子树就变成 \(u\) 的左子树。显然这样就可以满足笛卡尔树性质了。

如下图，图中红色框框部分就是我们始终维护的右链：

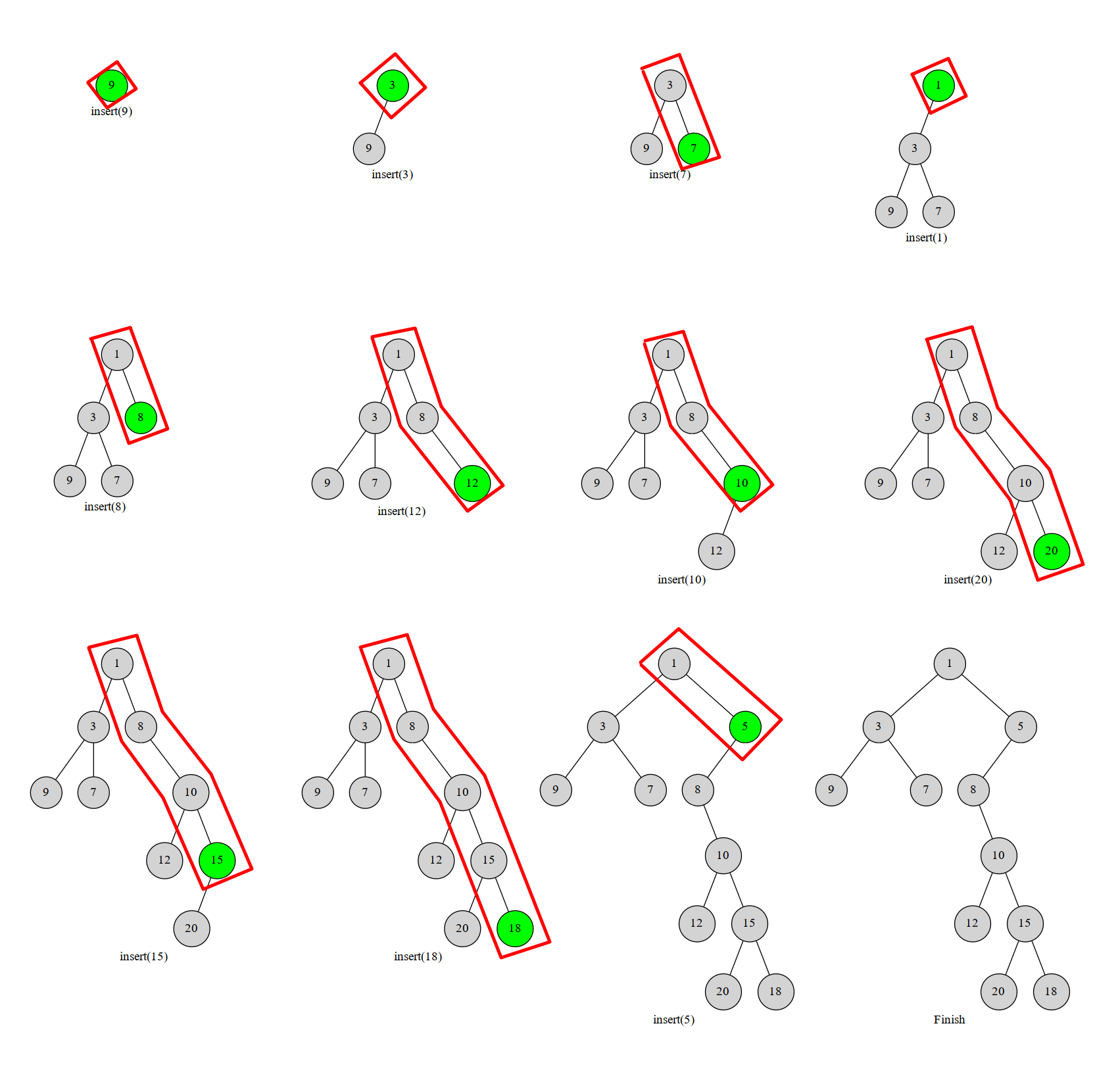
显然每个数最多进出右链一次。这个过程用栈维护，栈中维护当前笛卡尔树的右链上的结点。一个点不在右链上了就把它弹掉。这样每个点最多进出一次，复杂度 \(O(n)\)。

实现

for (int i = 1; i <= n; i++) {
  int k = top;
  while (k > 0 && h[stk[k]] > h[i]) k--;
  if (k) rs[stk[k]] = i;  // rs代表笛卡尔树每个节点的右儿子
  if (k < top) ls[i] = stk[k + 1];  // ls代表笛卡尔树每个节点的左儿子
  stk[++k] = i;
  top = k;
}

例题

CF1748E

HDU 1506 最大子矩形