本题解提供两种做法。
做法一
为了叙述方便,先引入 \(n\) 级母树的概念。
定义 \(1\) 级母树即为该子树被删去前,其所在的原来的完整的树。
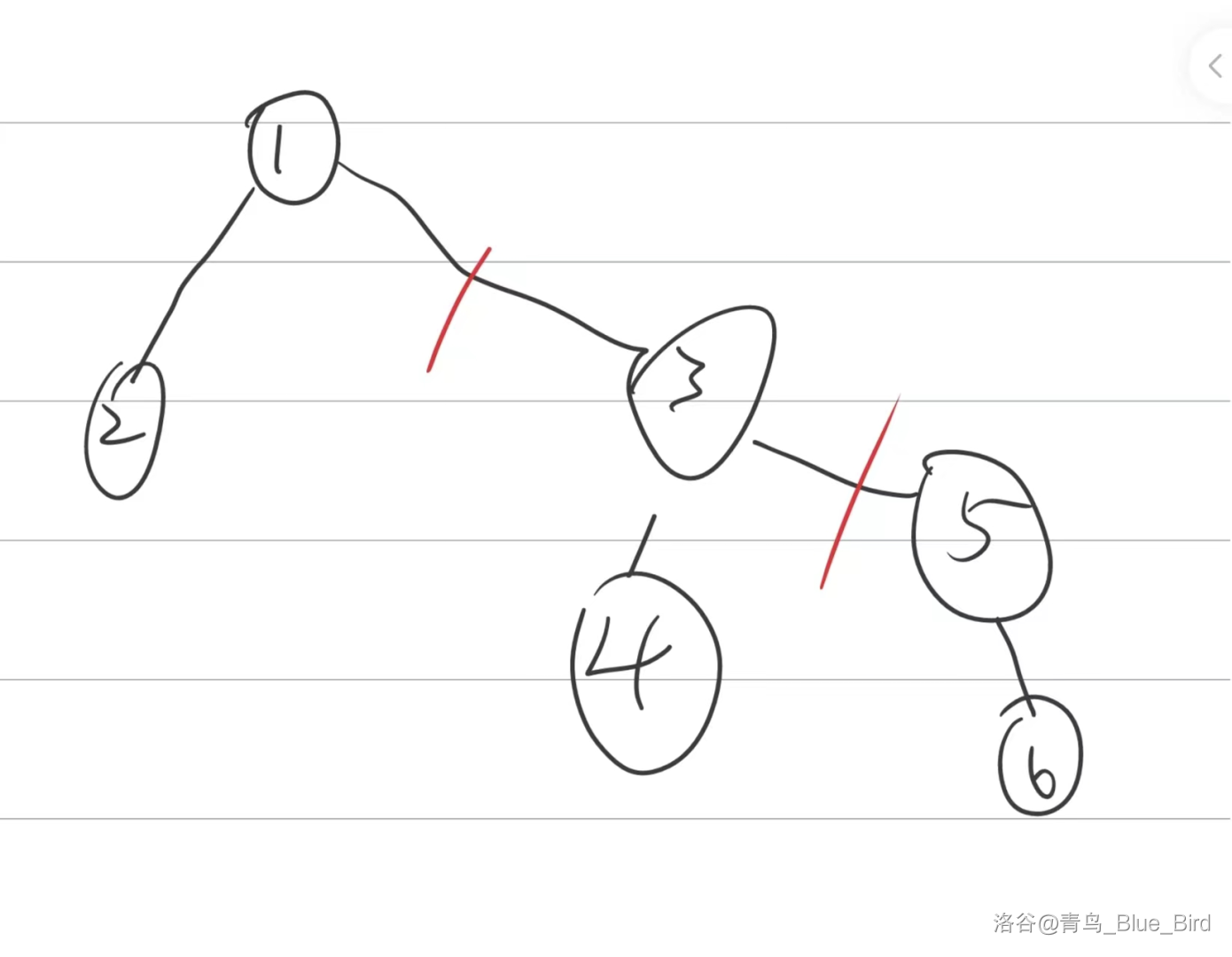
如下图,以 \(5\) 为根的一级母树为以 \(3\) 为根的原来的子树。类似地,以 \(1\) 为根的原来的树即为以 \(3\) 为根的树的 \(1\) 级母树以及以 \(5\) 为根的 \(2\) 级母树。
可以发现,题目中有这样一个条件:\(v \le 1000\)。也就是说,这棵树的初始情况是一个类菊花图。菊花图有一个很重要的性质,就是其深度非常浅。在题目中所给的条件下,假如我们从某一点按照其父亲一路跳至根节点,最多只能跳 \(1000\) 次。
利用这一性质,我们考虑维护每一个点的子树和 \(siz_u\)。那么,每一棵树的权值和即为其当前根节点的权值和。
考虑操作 \(1\), 我们直接模拟删去子树和。从现在被删树根节点 \(v\) 的父亲至其 \(1\) 级母树的根节点的路径上的所有点的子树和显然都要减掉 \(siz_v\)。一路上跳即可。
对于操作 \(2\), 我们计算出前后的改变量,从当前点到子树根节点上的 \(siz_i\) 显然都要加上改变量。一路上跳即可。
对于操作 \(3\), 按照上文所说,上跳到当前树的根节点查询即可。
代码:
#include <bits/stdc++.h>
using namespace std;
#define N 100010
#define ll long long
const int INF = 1e9;
template <class T>
inline void read(T& a){
T x = 0, s = 1;
char c = getchar();
while(!isdigit(c)){ if(c == '-') s = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + (c ^ '0'); c = getchar(); }
a = x * s;
return ;
}
struct node{
int u, v, next;
} t[N << 1];
int head[N];
int bian = 0;
inline void addedge(int u, int v){
t[++bian] = (node){u, v, head[u]}, head[u] = bian;
return ;
}
int n, m;
int a[N];
struct hehe{
int u, v;
} h[N];
int deth[N], siz[N], fa[N];
void dfs1(int u, int father){
fa[u] = father;
siz[u] = a[u];
deth[u] = deth[father] + 1;
for(int i = head[u]; i; i = t[i].next){
int v = t[i].v;
if(v != father){
dfs1(v, u);
siz[u] += siz[v];
}
}
return ;
}
map <int, int> del[N]; // 记录删边情况
signed main(){
// freopen("hh.txt", "r", stdin);
read(n), read(m);
for(int i = 1; i <= n; i++) read(a[i]);
for(int i = 1; i < n; i++){
int x, y;
read(x), read(y);
addedge(x, y);
addedge(y, x);
h[i].u = x, h[i].v = y;
}
dfs1(1, 0);
del[1][0] = del[0][1] = 1;
while(m--){
int opt, e, x, y;
read(opt);
if(opt == 1){
read(e);
int u = h[e].u;
int v = h[e].v;
if(deth[u] > deth[v]) swap(u, v);
del[u][v] = del[v][u] = 1;
while(!del[u][fa[u]]){
// printf("u: %d siz: %d\n", u, siz[v]);
siz[u] -= siz[v];
u = fa[u];
}
// printf("u: %d v: %d\n", u, siz[v]);
siz[u] -= siz[v];
}
else if(opt == 2){
read(x), read(y);
int d = y - a[x];
a[x] = y;
while(!del[x][fa[x]]){
siz[x] += d;
x = fa[x];
}
siz[x] += d;
}
else{
read(x);
while(!del[x][fa[x]]) x = fa[x];
cout << siz[x] << endl;
}
}
return 0;
}
方法二
考虑在原方法上进行升级。
思考:如果没有 \(v \le 1000\) 这个性质,我们暴力上跳的时间复杂度就会退化为 \(O(QN)\)。这显然是不行的。
可以发现,原方法的操作都是区间操作,于是考虑用树链剖分加线段树解决。
对于找当前点所在树的根,考虑如下性质:
- 根一定是当前点的父亲或者他自己。
- 在一条链上,各个点的 \(dfn\) 序是连续的,且深度浅的点一定小于深度大的点。
利用上面两个性质,可以发现,我们将删边操作下放到点,标记深度较深的那个点。查询时,断点一定与当前上跳的点在同一条链上,因此查询下标最大的那个即可。(即用线段树记录最大值。)
除了上面这个操作,剩下的上跳操作直接以树链剖分的区间修改替代即可。
#include <bits/stdc++.h>
using namespace std;
#define N 100010
#define ll long long
const int INF = 1e9;
template <class T>
inline void read(T& a){
T x = 0, s = 1;
char c = getchar();
while(!isdigit(c)){ if(c == '-') s = -1; c = getchar(); }
while(isdigit(c)){ x = x * 10 + (c ^ '0'); c = getchar(); }
a = x * s;
return ;
}
struct node{
int u, v, next;
} t[N << 1];
int head[N];
int bian = 0;
inline void addedge(int u, int v){
t[++bian] = (node){u, v, head[u]}, head[u] = bian;
return ;
}
int n, m;
int a[N];
struct hehe{
int u, v;
} h[N];
int dfn[N], id = 0, rev[N];
int son[N], deth[N], top[N], siz[N], fa[N];
int w[N];
void dfs1(int u, int father){
fa[u] = father;
siz[u] = 1;
w[u] = a[u];
deth[u] = deth[father] + 1;
int maxn = -INF;
for(int i = head[u]; i; i = t[i].next){
int v = t[i].v;
if(v != father){
dfs1(v, u);
siz[u] += siz[v];
w[u] += w[v];
if(siz[v] > maxn){
son[u] = v;
maxn = siz[v];
}
}
}
return ;
}
void dfs2(int u, int tp){
top[u] = tp;
dfn[u] = ++id; rev[id] = u;
if(!son[u]) return ;
dfs2(son[u], tp);
for(int i = head[u]; i; i = t[i].next){
int v = t[i].v;
if(v != fa[u] && v != son[u])
dfs2(v, v);
}
return ;
}
struct Segment_tree{
struct node{
int w;
bool del; // 这个点上面的那条边是否被删除
int id; // 被删除的最靠右的那个点
int add;
} t[N << 2];
#define lson (o<<1)
#define rson (o<<1|1)
inline void pushup(int o){
t[o].w = t[lson].w + t[rson].w;
t[o].del = t[lson].del | t[rson].del;
t[o].id = max(t[lson].id, t[rson].id);
return ;
}
inline void pushdown(int o, int l, int r){
int mid = l + r >> 1;
t[lson].add += t[o].add;
t[rson].add += t[o].add;
t[lson].w += t[o].add * (mid - l + 1);
t[rson].w += t[o].add * (r - mid);
t[o].add = 0;
return ;
}
void build(int o, int l, int r){
t[o].del = 0;
t[o].id = -1;
if(l == r){
t[o].w = w[rev[l]];
return ;
}
int mid = l + r >> 1;
build(lson, l, mid);
build(rson, mid + 1, r);
pushup(o);
return ;
}
int query_sum(int o, int l, int r, int in, int end){
if(l > end || r < in) return 0;
if(l >= in && r <= end) return t[o].w;
int mid = l + r >> 1;
pushdown(o, l, r);
return query_sum(lson, l, mid, in, end) + query_sum(rson, mid + 1, r, in, end);
}
void update2(int o, int l, int r, int x){ // 表示要把某个点上面的边删去
if(l > x || r < x) return ;
if(l == r && l == x){
t[o].del = 1;
t[o].id = l;
return ;
}
int mid = l + r >> 1;
pushdown(o, l, r);
update2(lson, l, mid, x);
update2(rson, mid + 1, r, x);
pushup(o);
return ;
}
int query_id(int o, int l, int r, int in, int end){ // 最靠右的被删除的点的 id
if(l > end || r < in) return -INF;
if(l >= in && r <= end) return t[o].id;
int mid = l + r >> 1;
pushdown(o, l, r);
return max(query_id(lson, l, mid, in, end), query_id(rson, mid + 1, r, in, end));
}
void update3(int o, int l, int r, int in, int end, int k){ // 区间加法
if(l > end || r < in) return ;
if(l >= in && r <= end){
t[o].add += k;
t[o].w += (r - l + 1) * k;
return ;
}
pushdown(o, l, r);
int mid = l + r >> 1;
update3(lson, l, mid, in, end, k); update3(rson, mid + 1, r, in, end, k);
pushup(o);
return ;
}
} tree;
int get_id(int x){ // 找断点,返回原始编号
while(top[x]){
int num = tree.query_id(1, 1, n, dfn[top[x]], dfn[x]);
if(num > 0) return rev[num];
x = fa[top[x]];
}
int num = tree.query_id(1, 1, n, dfn[top[x]], dfn[x]);
if(num > 0) return rev[num];
return 1;
}
void change(int x, int y, int k){ // x, y 路径上的全部加 k
while(top[x] != top[y]){
if(deth[x] < deth[y]) swap(x, y);
tree.update3(1, 1, n, dfn[top[x]], dfn[x], k);
x = fa[top[x]];
}
if(deth[x] > deth[y]) swap(x, y);
tree.update3(1, 1, n, dfn[x], dfn[y], k);
return ;
}
signed main(){
// freopen("hh.txt", "r", stdin);
read(n), read(m);
for(int i = 1; i <= n; i++) read(a[i]);
for(int i = 1; i < n; i++){
int x, y;
read(x), read(y);
addedge(x, y);
addedge(y, x);
h[i].u = x, h[i].v = y;
}
dfs1(1, 0);
dfs2(1, 0);
tree.build(1, 1, n);
while(m--){
int opt, e, x, y;
read(opt);
if(opt == 1){
read(e);
int u = h[e].u;
int v = h[e].v;
if(deth[u] > deth[v]) swap(u, v);
tree.update2(1, 1, n, dfn[v]);
int id = get_id(u);
int d = tree.query_sum(1, 1, n, dfn[v], dfn[v]);
change(id, u, -d); // 路径上的全部减掉 w[v] 值
}
else if(opt == 2){
read(x), read(y);
int d = y - a[x];
a[x] = y;
int id = get_id(x);
change(id, x, d); // 区间加上差值
}
else{
read(x);
int id = get_id(x);
cout << tree.query_sum(1, 1, n, dfn[id], dfn[id]) << endl;
}
}
return 0;
}