problem
令 \(f(i,j)\) 表示,在平面直角坐标系中,从 \((0,0)\) 出发,每次向上或向右走一步,到达 \((i,j)\) 的方案数,求:
\[\sum_{l_1\leq i\leq r_1}\sum_{l_2\leq j\leq r_2}f(i,j). \]\(n\leq 10^7\)。
solution
首先容斥是平凡的,拆成四个询问做。
结论一
\(f(i,j)=\binom{i+j}{i}.\)
证明:相当于是一个长为 \(i+j\) 的操作序列,要么上要么右,一共 \(i\) 个向右的操作插入序列中,就有这么多的方案数。
观察到 \(\binom{i+j}{i}=\binom{i+j}{j}\)。
结论二
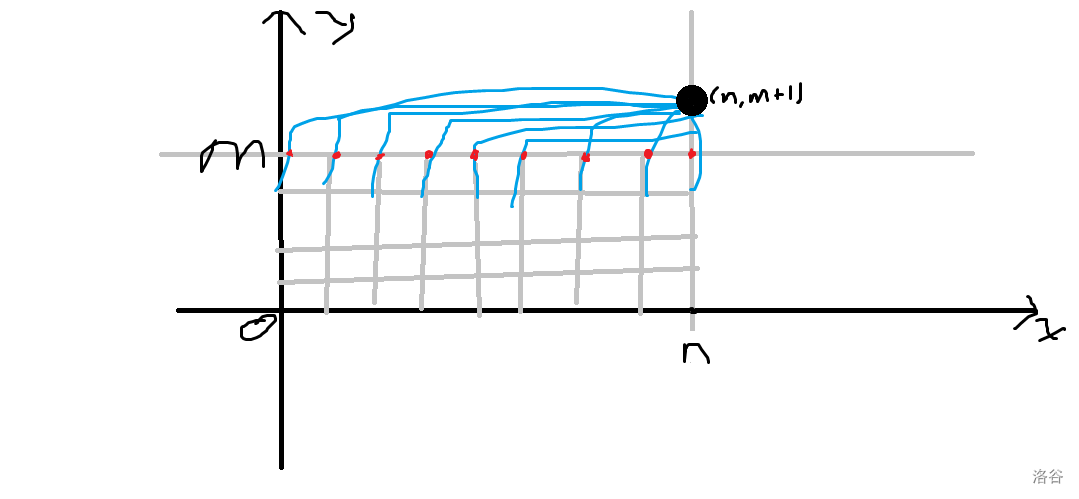
\(\sum_{0\leq i\leq n}f(i,m)=f(n,m+1).\)
你考虑这些路径往上走一步,之后一直往右走,这些路径和 \(f(n,m+1)\) 完全一致。
结论三
\[\begin{aligned} \sum_{0\leq i\leq n}\sum_{0\leq j\leq m}f(i,j) &=\sum_{0\leq i\leq n}f(i+1,m)\\ &=\sum_{1\leq i\leq n+1}f(i,m)\\ &=f(m+1,n+1)-f(0,m+1)\\ &=f(m+1,n+1)-1. \end{aligned}\]注意换元不要换错。
code
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int P=1e9+7;
LL qpow(LL a,LL b,int p=P){LL r=1;for(a%=P;b;b>>=1,a=a*a%p) if(b&1) r=r*a%p; return r;}
template<int N,int P> struct C_prime{
LL fac[N+10],ifac[N+10];
C_prime(){
for(int i=fac[0]=ifac[0]=1;i<=N;i++) fac[i]=fac[i-1]*i%P;
ifac[N]=qpow(fac[N],P-2,P);
for(int i=N-1;i>=1;i--) ifac[i]=ifac[i+1]*(i+1)%P;
}
LL operator()(int n,int m){return fac[n]*ifac[n-m]%P*ifac[m];}
};
C_prime<2000010,P> C;
LL f(int n,int m){return C(n+m,n);}
LL solve(int n,int m){
//\sum_{0\leq i\leq m} C(n,i)=C(n+1,m)
return (f(n+1,m+1)-1+P)%P;
}
int l,r,x,y;
int main(){
scanf("%d%d%d%d",&l,&x,&r,&y);
printf("%lld\n",(solve(r,y)-solve(r,x-1)-solve(l-1,y)+solve(l-1,x-1)+P+P)%P);
return 0;
}