时间序列分析：一种二次指数平滑法构建的纺织生产布料年产量线性预测模型

标签：预测平滑 years 布料 production SQL rn 0.6

目录

0 问题描述

1 符号规定与基本假设

0 问题描述

我国1974年——1981年布的产量如表1.1所示。

表1.1 我国1974年——1981年布的产量

年份	1974	1975	1976	1977	1978	1979	1980	1981
产量	80.8	94	88.4	101.5	110.3	121.5	134.7	142.7

（1）试用趋势移动平均法来建立布的年产量预测模型。

（2）分别取

建立布的直线指数平滑预测模型。

（3）计算模型拟合误差，比较三个模型的优劣。

（4）用最优的模型预测1982年和1985年布的产量

1 符号规定与基本假设

符号规定

基本假设

假设布的产量不受机器生产技术影响；

2. 假设只考虑布的产量不考虑除生产以外的其余因素影响。

2 模型的分析与建立

（1）建立布的年产量预测模型

（2）预测的标准误差为

（3）二次指数平滑法的计算公式为：

（4）

其中，表示一次指数的平滑值；

表示二次指数的平滑值

当时间序列从某时期开始具有直线趋势时，可以使用直线趋势模型

进行预测

若 $\alpha =0.3$ 则预测的标准误差为

若 $\alpha =0.6$ 则预测的标准误差为

（4）从标准差的角度考虑，选择 $\alpha =0.6$ 的二次指数平滑模型。

（5）本题选用 $\alpha =0.6$ 的二次指数平滑模型作为最优化的模型得到1982年和1985年的产量预测值为153亿米和183.03亿米。

3 模型的求解【基于SQL语言实现】

3.1 数据准备

create table production as
    (select stack(
                    8,
                    '1974', '80.8',
                    '1975', '94.0',
                    '1976', '88.4',
                    '1977', '101.5',
                    '1978', '110.3',
                    '1979', '121.5',
                    '1980', '134.7',
                    '1981', '142.7'
            ) as (years, production));

3.2 问题分析

步骤1：计算初始值。

select years
     , production
     , case
           when rn = 1 then cast(avg(production)
                                      over (order by years rows between  current row and 2 following ) as decimal(18, 4)) end init_production
     , rn
from (select years
           , production
           , row_number() over (order by years) rn
      from production) t

对计算得到的初始值进行NULL值补全，便于后续计算。得到如下SQL

  select years
         , production
         , last_value(init_production ignore nulls) over (order by YEARS) init_production
         , rn
    from (select years
               , production
               , case
                     when rn = 1 then cast(avg(production)
                                               over (order by years rows between current row and 2 following ) as decimal(18, 1)) end init_production
               , rn
          from (select years
                     , production
                     , row_number() over (order by years) rn
                from production) t
         ) t

步骤2：计算一次平滑值。

平滑值计算公式如下：

公式解释：

当 $\alpha =0.3$ t=1时,一次平滑值计算如下：

$^{S{1}^{(1)}}$ =0.3*y1+0.6* $\mathbf{^{{S_{0}}^{(1)}}}$

其中 $\mathbf{^{{S_{0}}^{(1)}}}$ 为步骤1计算的初始值，y1为原始产量值，结果为0.3*80.8 + 0.6*87.7 = 85.63

依次类推：递推如下

	表达式	展开式	合并表达式
1	0.3y1 + 0.6S0	0.3y1 + 0.6S0	0.3y1 + 0.6S0
2	0.3y2 + 0.6(0.3y1 + 0.6S0)	0.3y2+0.60.3y1+0.6^2S0	0.3(0.6y1 + y2) +0.6^2*S0
3	0.3y3 +0.6(0.3y2 + 0.6(0.3y1 + 0.6S0))	0.3y3 +0.6^20.3y1+0.6^10.3y2 +0.6^3S0	0.3(0.6^2y1+ 0.6^1y2 +y3)+0.6^3S0
4	… …	… …	… …
…
n

经过上述演绎，我们总结通项公式如下：

$\alpha * \sum_{i=1}^{n} \left ( 1-\alpha \right ) ^{n-i} * y{_{i}} +\left ( 1-\alpha \right )^{n}*S_{0}$

对上述迭代公式分析，我们可以看出指数平滑方法会将更大的权重赋到最近的观测值，对于更久远的观测值则会赋予较小的权重，权重的衰减速度由参数 $\alpha$ 控制。这里权重会以指数方式逐渐衰减到0。对于0到1之间的任何 $\alpha$ 值，随着时间向前推移，观察值的权重呈指数型下降，因此我们称之为“指数平滑”。当 $\alpha$ 越大时权重衰减的越快。当 $\alpha$ 越小时权重衰减的越慢，当 $\alpha=1$ , $\hat{X}_{t+1}=X_t$ 的极端情况，指数平滑的预测值等于最后一个预测值。

通过通项公式，我们就很容易利用SQL语言去求解，从而避免了复杂的递归运算。要解决上述公式中第一项，且能够控制项数（n -i）我们自然相到用自关联形式得到全量数据集后再进行行行比较。其中 $\alpha ^{n}$ 的求解我们用power(x,n)函数，结果值保留四位小数，分别计算当 $\alpha =0.3$ 及 $\alpha =0.6$ 时的一次平滑值。具体SQL如下：

with init as (
    select years
         , production
         , last_value(init_production ignore nulls) over (order by YEARS) init_production
         , rn
    from (select years
               , production
               , case
                     when rn = 1 then cast(avg(production)
                                               over (order by years rows between current row and 2 following ) as decimal(18, 1)) end init_production
               , rn
          from (select years
                     , production
                     , row_number() over (order by years) rn
                from production) t
         ) t
)
--计算一次平滑值
   , s1 as (select t1.years
                 , t1.production
                 , t1.init_production
                 , t1.rn
                 , cast(sum(case when t2.rn <= t1.rn then t2.production * power(0.7, t1.rn - t2.rn) else 0 end) * 0.3 +
                        power(0.7, t1.rn) * t1.init_production as decimal(18, 4)) s1_p3
                 , cast(sum(case when t2.rn <= t1.rn then t2.production * power(0.4, t1.rn - t2.rn) else 0 end) * 0.6 +
                        power(0.4, t1.rn) * t1.init_production as decimal(18, 4)) s1_p6
            from init t1,
                 init t2
            group by t1.years
                   , t1.production
                   , t1.init_production
                   , t1.rn
)
select *
from s1
order by YEARS;

步骤3：计算二次平滑值 $S_{t}^{(2)}$

二次平滑计算指标和一次平滑计算指标公式基本一样，只不过依赖于一次平滑值来计算，借助于步骤2的方法，我们得到如下SQL：

with init as (
    select years
         , production
         , last_value(init_production ignore nulls) over (order by YEARS) init_production
         , rn
    from (select years
               , production
               , case
                     when rn = 1 then cast(avg(production)
                                               over (order by years rows between current row and 2 following ) as decimal(18, 1)) end init_production
               , rn
          from (select years
                     , production
                     , row_number() over (order by years) rn
                from production) t
         ) t
)
--计算一次平滑值
, s1 as (select t1.years
              , t1.production
              , t1.init_production
              , t1.rn
              , cast(sum(case when t2.rn <= t1.rn then t2.production * power(0.7, t1.rn - t2.rn) else 0 end) * 0.3 +
                     power(0.7, t1.rn) * t1.init_production as decimal(18, 4)) s1_p3
              , cast(sum(case when t2.rn <= t1.rn then t2.production * power(0.4, t1.rn - t2.rn) else 0 end) * 0.6 +
                     power(0.4, t1.rn) * t1.init_production as decimal(18, 4)) s1_p6
         from init t1,
              init t2
         group by t1.years
                , t1.production
                , t1.init_production
                , t1.rn
)
--计算二次平滑值
, s2 as (select t1.years
              , t1.production
              , t1.init_production
              , t1.rn
              , t1.s1_p3
              , t1.s1_p6
              , cast(sum(case when t2.rn <= t1.rn then t2.s1_p3 * power(0.7, t1.rn - t2.rn) else 0 end) * 0.3 +
                     power(0.7, t1.rn) * t1.init_production as decimal(18, 4)) s2_p3
              , cast(sum(case when t2.rn <= t1.rn then t2.s1_p6 * power(0.4, t1.rn - t2.rn) else 0 end) * 0.6 +
                     power(0.4, t1.rn) * t1.init_production as decimal(18, 4)) s2_p6
         from s1 t1,
              s1 t2
         group by t1.years
                , t1.production
                , t1.init_production
                , t1.rn
                , t1.s1_p3
                , t1.s1_p6
)
select *
from s2
order by YEARS;

步骤4：计算直线趋势模型的系数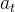 $a_{t}$ 及 $^{b_{t}}$

基于步骤3，按照给出的公式计算拟合的一次线性趋势模型的系数，具体SQL如下：

with init as (
    select years
         , production
         , last_value(init_production ignore nulls) over (order by YEARS) init_production
         , rn
    from (select years
               , production
               , case
                     when rn = 1 then cast(avg(production)
                                               over (order by years rows between current row and 2 following ) as decimal(18, 1)) end init_production
               , rn
          from (select years
                     , production
                     , row_number() over (order by years) rn
                from production) t
         ) t
)
--计算一次平滑值
, s1 as (select t1.years
              , t1.production
              , t1.init_production
              , t1.rn
              , cast(sum(case when t2.rn <= t1.rn then t2.production * power(0.7, t1.rn - t2.rn) else 0 end) * 0.3 +
                     power(0.7, t1.rn) * t1.init_production as decimal(18, 4)) s1_p3
              , cast(sum(case when t2.rn <= t1.rn then t2.production * power(0.4, t1.rn - t2.rn) else 0 end) * 0.6 +
                     power(0.4, t1.rn) * t1.init_production as decimal(18, 4)) s1_p6
         from init t1,
              init t2
         group by t1.years
                , t1.production
                , t1.init_production
                , t1.rn
)
--计算二次平滑值
, s2 as (select t1.years
              , t1.production
              , t1.init_production
              , t1.rn
              , t1.s1_p3
              , t1.s1_p6
              , cast(sum(case when t2.rn <= t1.rn then t2.s1_p3 * power(0.7, t1.rn - t2.rn) else 0 end) * 0.3 +
                     power(0.7, t1.rn) * t1.init_production as decimal(18, 4)) s2_p3
              , cast(sum(case when t2.rn <= t1.rn then t2.s1_p6 * power(0.4, t1.rn - t2.rn) else 0 end) * 0.6 +
                     power(0.4, t1.rn) * t1.init_production as decimal(18, 4)) s2_p6
         from s1 t1,
              s1 t2
         group by t1.years
                , t1.production
                , t1.init_production
                , t1.rn
                , t1.s1_p3
                , t1.s1_p6
)
--计算直线趋势模型系数
select years
     , production
     , init_production
     , rn
     , s1_p3
     , s1_p6
     , s2_p3
     , s2_p6
     , cast(case when rk=1 then 2*s1_p3 - s2_p3 else 0 end as decimal(18,2)) a_p3
     , cast(case when rk=1 then 2*s1_p6 - s2_p6 else 0 end as decimal(18,2)) a_p6
     , cast(case when rk=1 then (s1_p3 - s2_p3)*(0.3/(1-0.3)) else 0 end as decimal(18,2)) b_p3
     , cast(case when rk=1 then (s1_p6 - s2_p6)*(0.6/(1-0.6)) else 0 end as decimal(18,2))  b_p6
from (select years
           , production
           , init_production
           , rn
           , s1_p3
           , s1_p6
           , s2_p3
           , s2_p6
           , row_number() over (order by rn desc) rk
      from s2
     ) t
;

步骤5:构建线性预测模型进行结果预测

根据步骤4计算的结果，得到线性方程式如下

当 $\alpha =0.3$ 时

$y_m{} = 137.44 + 6.43 m, m=1,2... ...$

当 $\alpha =0.6$ 时

$y_m{} = 142.99 + 10.01 m, m=1,2... ...$

采用0.6的系数计算

1982年的预测产量为：142.99+10.01=153

1985年的预测产量为：142.99+10.01*4=183.03

3.3 结果分析及问题讨论

本题第一问建立出布的年产量预测模型为。本体第二问建立布的直线指数预测模型为。本题第三问从标准差的角度考虑，选择 $\alpha =0.6$ 的二次指数平滑模型。本题第四问选用 $\alpha =0.6$ 的二次指数平滑模型作为最优化的模型得到1982年和1985年的产量预测值为153 亿米和183.03亿米。

（1）本模型适合场景：产量预测、计划需求预测、企业营收预测等

（2）对于平滑系数的确定

在指数平滑法中，预测成功的关键是a的选择。a的大小规定了在新预测值中新数据和原预测值所占的比例。a值愈大，新数据所占的比重就愈大，原预测值所占比重就愈小，反之亦然。

对于平滑系数的选取，阅读相关文献后，你会发现一些经验值：

当需求历史比较稳定时，选择较小的α值，0.05～0.2；
·当需求历史有波动，但长期趋势没有大的变化时，可选择稍大的α值，0.1～0.4；
·当需求历史波动很大，呈现明显且迅速的上升或下降趋势时，宜选取较大的α值，0.6～0.8；
·当需求历史是上升或者下降序列时，α宜取较大值，0.6～1。

但是，需求多稳定才算稳定，波动多大才算大，这很难量化，各人理解也不相同。比如有家企业的营收每年翻倍，计划经理认为业务波动很大，在她的逻辑里，增长本身就意味着波动，α应该取0.6～0.8。但我研究了一些产品后，发现α实际上取0.3最合适，也就是说业务的变动没有想象的大。

在具体实践中，平滑系数可按以下方式择优：

（1）先把需求历史做成折线图，时间为横轴，需求历史为纵轴，大致判断需求历史的稳定性，以及是否有趋势、季节性；

（2）然后参照上述经验值，确定平滑系数的大致范围；

（3）最后套用几个不同的α值，一般每个相差0.05，看哪个的预测准确度最高，哪个就是最优的平滑系数。这一般会通过复盘的方式进行，比如复盘过去13周的预测，计算每周的均方误差，然后求得13周的平均均方误差，据此判断预测的准确度。

（3） 的选择

对于 $S_0$ 我们可以有两种选择方法：

选取第一个时刻的实际值作为 $S_0$ 。
使用前N个实际值的平均值作为 $S_0$ 。

（4） 指数平滑法的缺点：

• （1）对数据的转折点缺乏鉴别能力，但这一点可通过调查预测法或专家预测法加以弥补。

• （2）长期预测的效果较差，故多用于短期预测。

（5）指数平滑法的优点：

•    （1）对不同时间的数据的非等权处理较符合实际情况。

•    （2）实用中仅需选择一个模型参数a 即可进行预测，简便易行。

•    （3）具有适应性，也就是说预测模型能自动识别数据模式的变化而加以调整。

4 小结

文章通过纺织生产布料的年产量预测这一场景进行引入，利用二次指数平滑法构建线性预测模型该模型的实现主要采用SQL语言，通过均方根误差（RMSE）分析表明，当平滑系数 $\alpha =0.6$ 时，模型误差较小，相对准确。

在备品备件领域，特别是高值慢动的产品，需求很不频繁，一旦发生，往往意味着很多（小概率事件不容易发生，一旦发生则意味着不再是小概率事件）：是不是这批设备用到一定年限了，需要更换相应的备件，或者产线在做什么预防性维修等。简单指数平滑法能够更迅速地捡起这一信号，尽快调整预测，驱动供应链尽快响应。

指数平滑法未来挑战

简单指数平滑法虽然只有一个系数，但该平滑系数的优化不易。常见的误区是高估业务的变动性，取较大的平滑系数，灵敏度是足够了，但有可能过度反应，放大“杂音”，降低预测准确度。
简单指数平滑法适合短期预测，比如适合预测下一期的补货。但如果预测的时段长了，虽然我们假定未来每期的需求都一样，都等于下一期的预测，但时间跨度越长，这个假定越难成立。
跟移动平均法一样，简单指数平滑法是滞后的，一旦需求表现出趋势、季节性等，指数平滑法就一直处于“追赶”状态，我们得考虑更合适的指数平滑模型，比如霍尔特指数平滑（趋势）模型和霍尔特–温特（季节性加趋势）模型。

附录：预测通项公式完整推导过程

最简单的指数平滑方法被称为“简单指数平滑”，这种方法适用于预测没有明显趋势或季节特征的数据。简单指数平滑通过一个递归式来获取所有观测数据的权重,并在此基础上做出对未来的预测。简单指数平滑的递归式定义：

$S_t = \alpha X_t + (1-\alpha) S_{t-1} \quad \text{where} \quad \alpha \in (0,1)$

如果我们将上面的递归式展开可以得到如下的等式：

$S_t = \alpha X_t + (1-\alpha) S_{t-1}\\\\= \alpha X_t + \alpha(1-\alpha) X_{t-1} + \alpha(1-\alpha)^2 X_{t-2}+\cdots+ \alpha(1-\alpha)^{t-1} X_1+ (1-\alpha)^tS_0$

最后我们将此递归展开式进行整理后得到：

$S_t = \sum_{i=0}^{t-1} \alpha(1-\alpha)^i X_{t-i} + (1-\alpha)^tS_0$

预测公式：

$\hat{X}_{t+h} = S_t = \sum_{i=0}^{t-1} \alpha(1-\alpha)^i X_{t-i} + (1-\alpha)^tS_0 \quad \text{where} \quad h=1,2,3\cdots$

其中

$S_t$ ：表示t+h 时刻的预测值即 $\hat{X}_{t+h} = S_t \quad \text{where} \quad h=1,2,3\cdots$
$X_t$ : 表示时刻 t 的实际观测值.
$\alpha:$ 是平滑参数 $0 \le \alpha \le 1$
$S_0:$ : 它是递归展开式的初始化参数。

如果您觉得本文还不错，对你有帮助，那么不妨可以关注一下我的数字化建设实践之路专栏，这里的内容会更精彩。

专栏原价99，现在活动价59.9，按照阶梯式增长，还差5个人上升到69.9，最终恢复到原价。

专栏优势：
（1）一次收费持续更新。

（2）实战中总结的SQL技巧，帮助SQLBOY 在SQL语言上有质的飞越，无论你应对业务难题及面试都会游刃有余【全网唯一讲SQL实战技巧，方法独特】

（3）实战中数仓建模技巧总结，让你认识不一样的数仓。【数据建模+业务建模，不一样的认知体系】（如果只懂数据建模而不懂业务建模，数仓体系认知是不全面的）

（4）数字化建设当中遇到难题解决思路及问题思考。

我的专栏具体链接如下：

数字化建设通关指南_莫叫石榴姐的博客-CSDN博客

https://blog.csdn.net/godlovedaniel/category_12706766.html

标签：预测,平滑,years,布料,production,SQL,rn,0.6
From： https://blog.csdn.net/godlovedaniel/article/details/143226634

	表达式	展开式	合并表达式
1	0.3y1 + 0.6S0	0.3y1 + 0.6S0	0.3y1 + 0.6S0
2	0.3y2 + 0.6(0.3y1 + 0.6S0)	0.3y2+0.60.3y1+0.6^2S0	0.3(0.6y1 + y2) +0.6^2*S0
3	0.3y3 +0.6(0.3y2 + 0.6(0.3y1 + 0.6S0))	0.3y3 +0.6^20.3y1+0.6^10.3y2 +0.6^3S0	0.3(0.6^2y1+ 0.6^1y2 +y3)+0.6^3S0
4	… …	… …	… …
…
n

时间序列分析：一种二次指数平滑法构建的纺织生产布料年产量线性预测模型 | 基于SQL语言实现

0 问题描述

1 符号规定与基本假设

2 模型的分析与建立

3 模型的求解【基于SQL语言实现】

3.1 数据准备

3.2 问题分析

步骤1：计算初始值。

步骤2：计算一次平滑值。

步骤3：计算二次平滑值 $S_{t}^{(2)}$

步骤4：计算直线趋势模型的系数 $a_{t}$ 及 $^{b_{t}}$

步骤5:构建线性预测模型进行结果预测

3.3 结果分析及问题讨论

4 小结

指数平滑法未来挑战

附录：预测通项公式完整推导过程

相关文章

赞助商

阅读排行

时间序列分析：一种二次指数平滑法构建的纺织生产布料年产量线性预测模型 | 基于SQL语言实现

0 问题描述

1 符号规定与基本假设

2 模型的分析与建立

3 模型的求解 【基于SQL语言实现】

3.1 数据准备

3.2 问题分析

步骤1：计算初始值。

步骤2：计算一次平滑值。

步骤3：计算二次平滑值

步骤4：计算直线趋势模型的系数 及

步骤5:构建线性预测模型进行结果预测

3.3 结果分析及问题讨论

4 小结

指数平滑法未来挑战

附录：预测通项公式完整推导过程

相关文章

赞助商

阅读排行

3 模型的求解【基于SQL语言实现】

步骤3：计算二次平滑值 $S_{t}^{(2)}$

步骤4：计算直线趋势模型的系数 $a_{t}$ 及 $^{b_{t}}$