前缀和及差分
前缀和
一维前缀和
定义
一维前缀和,就是数组前若干项的和。
我们对于前缀和数组的定义非常广泛,
例如定义 \(S(x)\) 表示数组 \(A(x)\) 的前缀和,
定义 \(A(l,r)\) 表示 \(A(l)+A(l+1)+\dots+A(r)\),
-
\(S(x)=A(0,x)\);
-
\(S(x)=A(1,x)\);
-
\(S(x)=A(1,x-1)\);
-
\(S(x)=A(0,x-1)\)。
都是可以的,只不过我们一般用前两个。
实现
我们可以枚举每一个元素,用,
\[S(x)=\sum_{i=1}^xA(i) \]表示前缀和,那么有递推式,
\[S(x)=S(x-1)+A(x),S(0)=0 \]这是显然的。
C++ 语言中自带的前缀和函数为 std::partial_sum,
- 形如:
partial_sum(begin, end, dist), - 表示
[begin, end)的前缀和放在 dist 开始的位置, - 返回终止迭代器。
-
实现 1
最经典的方法,
for (int i = 1; i <= n; ++i) S[i] = S[i - 1] + A[i];这种方法会保留原数组的内容。
-
实现 2
我们在原数组直接进行操作,
for (int i = 1; i <= n; ++i) A[i] += A[i - 1];这种方法不会保留原数组的内容,但是省空间。
-
实现 3
冷知识,
for (int i = 1; i < n; ++i) A[i + 1] += A[i];的速度要比前一个略快,因为编译器对前一个的优化是不到位的。
这个问题在 GCC 12 修复,NOI-Linux 中的 GCC 9 是未修复的版本[1]。
-
实现 4
使用 STL 函数,
partial_sum(A + 1, A + n + 1, A + 1);进行原地的前缀和。
应用
我们可以利用一维前缀和,进行不带修的 \(\mathcal O(1)\) 区间求和。
具体的,
\[S(l,r)=S(r)-S(l-1) \]这是显然的。
另外,修改复杂度为 \(\mathcal O(n)\),一般不会使用。
如果要修改,一般会配合概率相关,
如果进行 \(m\) 次操作,每次操作修改的概率是 \(1/n\),
那么就可以进行 \(\mathcal O(n)\) 的修改,因为这样均摊的复杂度依旧是 \(\mathcal O(m)\) 的。
二维前缀和
定义
我们直接取比较常见的定义,
\[S(x,y)=\sum_{i\le x}\sum_{j\le y}A(i,j) \]几何意义就是,将二维平面划分为网格,建立平面直角坐标系。
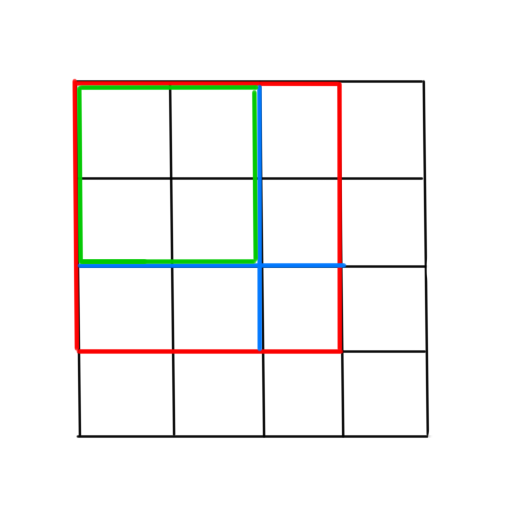
那么,其前缀和平面的每一个点表示的就是,
从原点(此处是 \((1,1)\))到这个点的矩形的权值和。
实现
那么可以容斥解决,
\[S(x,y)=A(x,y)+S(x-1,y)+S(x,y-1)-S(x-1,y-1) \]这么做是最直观的。
应用
不带修子区间求和问题,具体的,
\[S(a,b,c,d)=S(c,d)-S(c,b-1)-S(a-1,d)+S(a-1,b-1) \]同样修改复杂度是 \(\mathcal O(n^2)\) 的重构。
高维前缀和
定义
代数表示为,
\[S(x_1,x_2\dots,x_k)=\sum_{i_1\le x_2}\sum_{i_2\le x_2}\dots\sum_{i_k\le x_k}A(i_1,i_2,\dots,i_k) \]一般只有三维前缀和是具有直观的几何意义的,但是我们也不去讨论。
实现
假设我们要求边长为 \(n\) 的 \(k\) 维超正方体的前缀和,
那么,如果继续使用容斥原理,复杂度将是 \(\mathcal O(n^k2^k)\) 的,也就是说项数为 \(2^k\) 的。
这显然是难以接受的(在 \(3\) 维中就有 \(8\) 项,这是很恐怖的)。
但是,我们有一个类似 DP 的求解高维前缀和的方法,我们下面仅以 \(3\) 维为例。
我们先枚举每一个维度,然后对这个维度下进行前缀和,那么复杂度就是 \(\mathcal O(n^kk)\) 的。
尽管这个复杂度依然很大,但是一般来说我们很少讨论 \(4\) 维以上的前缀和,因此还是凑合的。
板子题:AtCoder - abc366_d - Cuboid Sum Query。
// 读入
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
for (int k = 1; k <= n; ++k)
cin >> s[i][j][k];
// 将第一维前缀和
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
for (int k = 1; k <= n; ++k)
s[i][j][k] += s[i - 1][j][k];
// 将第二维前缀和
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
for (int k = 1; k <= n; ++k)
s[i][j][k] += s[i][j - 1][k];
// 将第三维前缀和
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
for (int k = 1; k <= n; ++k)
s[i][j][k] += s[i][j][k - 1];
应用
高维子超立方体求和,我们发现式子会很复杂,
于是我们依然类似 DP 的,将每一个维度拆分考虑。
依旧以上一题的三维为例,我们使用 C++ 的函数重载特性,
int query(int x, int y, int z) {
return s[x][y][z];
}
// 拆分第三维
int query(int x, int y, int lz, int rz) {
return query(x, y, rz) - query(x, y, lz - 1);
}
// 拆分第二维
int query(int x, int ly, int ry, int lz, int rz) {
return query(x, ry, lz, rz) - query(x, ly - 1, lz, rz);
}
// 拆分第一维
int query(int lx, int rx, int ly, int ry, int lz, int rz) {
return query(rx, ly, ry, lz, rz) - query(lx - 1, ly, ry, lz, rz);
}
这就比较好理解了。
差分
一维差分
定义
我们定义 \(D\) 为 \(A\) 的差分,即,
\[D(x)=A(x)-A(x-1) \]对于一个长度为 \(n\) 的序列 \(A[1,n]\),有,
\[D(x)=\begin{cases} A(x)-A(x-1)&x\in[2,n]\\ A(x)&x=1 \end{cases} \]性质:
-
数组 \(A\) 的前缀和 \(S\) 的差分是 \(A\);
-
数组 \(A\) 的差分 \(D\) 的前缀和是 \(A\)。
即,差分与前缀和互为逆运算。
-
构造性的理解:
我们构造差分数组的过程,也可以构造性的来看:
我们知道数组 \(A\),求一个数组 \(D\) 使得 \(D\) 的前缀和是 \(A\)。
考虑 \(A(x)\) 的所有贡献,发现我们进行前缀和的时候就会对它及其后面所有数造成贡献。
因此,我们对于 \(A(x)\),进行操作,
\[\begin{aligned} D(x)&\gets D(x)+A(x)\\ D(x+1)&\gets D(x+1)-A(x) \end{aligned} \]那么进行前缀和的时候就会消去多余的贡献了。
然后再反过来考虑每一个 \(D(x)\) 受到了什么贡献,容易发现就是,
\[D(x)=A(x)-A(x-1) \]这就是一种构造性的理解。
C++ 中也有差分的函数 std::adjacent_difference,
- 形如:
adjacent_difference(begin, end, dist), - 表示
[begin, end)对相邻两项的差值, - 放在
dist + 1开始的位置,返回终止迭代器。
应用
类似上文构造性的方法,我们可以利用差分数组,进行 \(\mathcal O(1)\) 的区间加,\(\mathcal O(n)\) 的单点查询:
-
对 \([l,r]\) 加上 \(x\):令 \(D(l)\gets D(l)+x,D(r+1)\gets D(r+1)-x\);
-
查询:对数组跑一遍前缀和,发现多余的贡献都被消除了,那么就可以直接访问。
二维差分
定义
我们可以直接定义 \(D\) 为 \(A\) 的二维差分,当且仅当 \(D\) 的二维前缀和为 \(A\)。
考虑构造,我们发现只需要令,
\[\begin{aligned} D(x,y)&\gets D(x,y)+A(x,y)\\ D(x+1,y)&\gets D(x+1,y)-A(x,y)\\ D(x,y+1)&\gets D(x,y+1)-A(x,y)\\ D(x+1,y+1)&\gets D(x+1,y+1)+A(x,y) \end{aligned} \]这样子就是正确的。
应用
类似一维,可以进行 \(\mathcal O(1)\) 的子矩阵加,\(\mathcal O(n^2)\) 的单点查询。
具体略。
树上问题
一般讨论点权和边权。
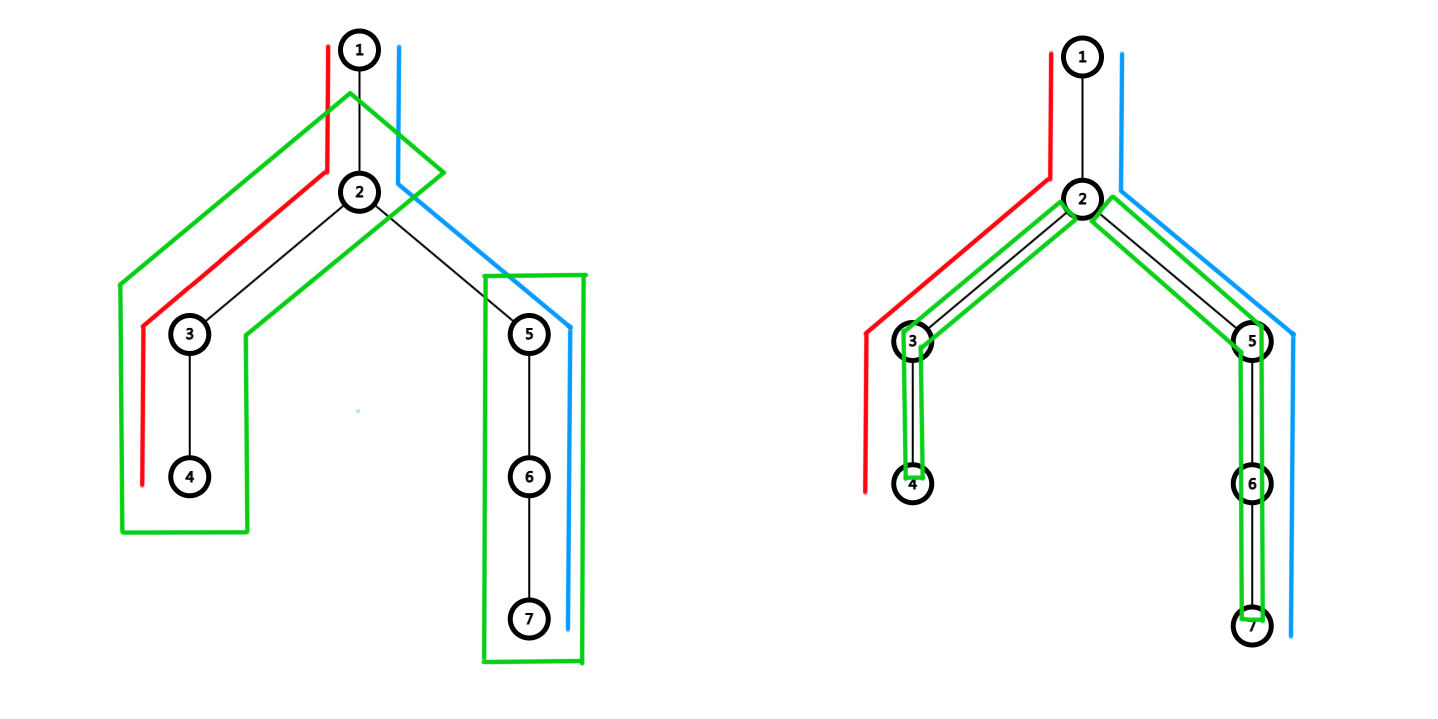
对于边权通常比较难处理,会下方到点权,下文所说边权均为下放到点权后的。
树上前缀和
设 \(S(u)\) 表示从根到节点 \(u\) 经过的所有权值和。
设 \(S(x,y)\) 表示 \(x\to y\) 路径上的权值和,
-
若是点权,\(S(x,y)=S(x)+S(y)-S(\mathrm{LCA})-S(\mathrm{fa_{LCA}})\);
-
若是边权,\(S(x,y)=S(x)+S(y)-2S(\mathrm{LCA})\)。
树上差分
树上差分可以用于在树上快速修改然后统一查询。
一般我们会对一条链进行操作,假设我们对 \(x\to y\) 路径上的权值进行修改,
-
若是点权,我们对 \(x,y\) 加 \(1\) 倍,对 \(\mathrm{LCA}\) 减 \(1\) 倍,对 \(\mathrm{fa_{LCA}}\) 减 \(1\) 倍即可。
-
若是边权,我们对 \(x,y\) 加 \(1\) 倍,对 \(\mathrm{LCA}\) 减 \(2\) 倍即可。
其他前缀
前缀积
我们设,
\[P(x)=\prod_{i=1}^xA(i) \]前缀积一般是满足可差分性的,但是取模后就不一定了。
例如,在某一处的前缀积关于模数不存在乘法逆元的情况。
我们只讨论满足可差分性的,那么有,
\[P(l,r)=\frac{P(r)}{P(l-1)} \]特殊的,我们定义 \(P(0)=1\)。
可以用于求一段区间的乘积,但是不常用,因为乘大了自然需要取模。
前缀最大最小值
以最大值为例。
我们设,
\[M(x)=\max_{i=1}^xA(i) \]这显然不满足可差分性,因此不能求区间的结果。
但是依然应用很广泛。
前缀异或和
我们设,
\[R(x)=\bigoplus_{i=1}^xA(i) \]其中 \(\oplus\) 运算符表示按位异或 \(\operatorname{xor}\) 运算。
注意到这是满足可差分性的,因为 \(x\operatorname{xor}x=0\),因此,
\[R(l,r)=R(r)\bigoplus R(l-1) \]这个也存在应用。
还有一些好玩的详见异或哈希算法。
参考 2024 国家集训队论文 宋佳兴《论现代硬件上的常数优化》。 ↩︎