1. 算法简介
先来看一个很现实的问题:
就拿 [luogu]P3372【模板】线段树 1 这道题为例。
按常规做法,应该是用普通线段树 + \(lazytag\) 即可,但这样做代码较长,达到了 \(118\) 行。
而如果用树状数组去做,只用 \(63\) 行就能搞定,用时更短,代码也很好理解。
以下是数据对比:

很明显,在两者都开了 \(O_2\) 的情况下,树状数组在时间、空间、代码长度上完胜线段树!!!
Q: 树状数组这么好用,为什么不直接用树状数组完全替代线段树呢?
这就又要讲到树状数组的特性:它是一颗‘前缀树’。也就是树状数组只能用于维护前缀信息,如前缀和、前缀积、前缀异或等等。想要维护区间信息,就必须要使维护的区间信息有 ‘可减性’(这里和线段树是相反的,线段树需要满足 ‘可合并性’)。在一些区间信息无 ‘可减性’ 的时候,树状数组就无法胜任。例如区间最值、区间第 \(k\) 小等等,普通的树状数组就无能为力了。
Q: 学习树状数组需要哪些前置知识呢?
二进制、位运算、前缀和,差分。最好有线段树基础。
到现在,大家应该对树状数组有了一定的了解还不是很了解,那就来由我来给大家讲讲树状数组的知识吧!
2. 算法实现
一个树状数组大概长这样(以区间和为例)
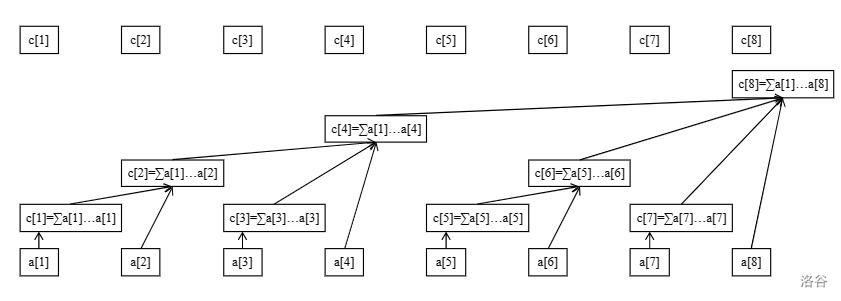
可以观察到,树状数组 \(c_i\) \((1 \le i \le n)\) 所管辖的范围为 \([i,i-lowbit(i)+1]\),其中 \(lowbit(i)\) 表示 \(i\) 在二进制下末尾 \(0\) 的。
比如 \(12_{(10)}=1100_{(2)}\),则 \(lowbit(12_{(10)})=100_{(2)}=4_{(10)}\).
然后进行修改和查询操作的时候,可以利用 \(lowbit\) 跳跃节点。(参考例图)
比如要将 \(1\) 号节点加 \(k\),先将 \(1\) 号节点加上 \(k\);然后跳跃至 \(1+lowbit(1)=2\) 号点,加上 \(k\);继续跳跃至 \(2+lowbit(2)=4\) 号点,加上 \(k\),最后跳跃至 \(4+lowbit(4)=8\) 号点,加上 \(k\)。
查询也是如此,只要依次跳跃至查询节点即可。
\(lowbit\) 函数实现:
int lb(int x) {
return x & -x;
}
单点修改实现:
void add(int x, int k) {
for (int i = x; i <= n; i += lb(i)) {
t[i] += k;
}
}
区间查询 \([1,x]\) 实现:
int qry(int x) {
int res = 0;
for (int i = x; i; i -= lb(i)) {
res += t[i];
}
return res;
}
2.1 单点加区间和
直接套用树状数组的单点加,区间和的操作即可。
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N = 5e5 + 10;
int n, m, t[N];
int lb(int x) {
return x & -x;
}
void add(int x, int k) {
for (int i = x; i <= n; i += lb(i)) {
t[i] += k;
}
}
int qry(int x) {
int res = 0;
for (int i = x; i; i -= lb(i)) {
res += t[i];
}
return res;
}
signed main() {
n = read(), m = read();
For(i,1,n) add(i, read());
while(m--) {
int op, x, y;
op = read(), x = read(), y = read();
if(op == 1) add(x, y);
else cout << qry(y) - qry(x - 1) << '\n';
}
return 0;
}
2.2 区间加单点和
树状数组维护差分。
每一次操作在差分序列上的 \(l\) 处加,\(r+1\) 处减等价在原序列的 \([l,r]\) 加。单点和即求 \([1,x]\) 的差分序列前缀和。
点击查看代码
#include <bits/stdc++.h>
#define ll long long
#define H 19260817
#define rint register int
#define For(i,l,r) for(rint i=l;i<=r;++i)
#define FOR(i,r,l) for(rint i=r;i>=l;--i)
#define MOD 1000003
#define mod 1000000007
using namespace std;
inline int read() {
rint x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
return x*f;
}
const int N = 5e5 + 10;
int n, m, t[N], a[N];
int lb(int x) {
return x & -x;
}
void add(int x, int k) {
for (int i = x; i <= n; i += lb(i)) {
t[i] += k;
}
}
int qry(int x) {
int res = 0;
for (int i = x; i; i -= lb(i)) {
res += t[i];
}
return res;
}
signed main() {
n = read(), m = read();
For(i,1,n) a[i] = read();
For(i,1,n) add(i, a[i] - a[i-1]);
while(m--) {
int op, x, y, k;
op = read();
if(op == 1) {
x = read(), y = read(), k = read();
add(x, k);
add(y+1, -k);
} else {
x = read();
cout << qry(x) << '\n';
}
}
return 0;
}
2.3 区间加区间和
维护差分序列 \(d_i\),则修改操作为单点,查询操作为查询 \(\sum\limits_{i=l}^r\sum\limits_{j=1}^i d_j\)。
然后拆式子 \(sum(x)=\sum\limits_{i=1}^x\sum\limits_{j=1}^i d_j=\sum\limits_{i=1}^x(x-i+1)d_i=x\sum\limits_{i=1}^xd_i+\sum\limits_{i=1}^xd_i\times (i+1)\)
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define For(i,l,r) for(int i=l;i<=r;++i)
#define FOR(i,r,l) for(int i=r;i>=l;--i)
using namespace std;
const int N = 1e5 + 10;
int n, m, a[N], t1[N], t2[N];
int lb(int x) {
return x & -x;
}
void add(int x, int k) {
for (int i = x; i <= n; i += lb(i)) {
t1[i] += k;
t2[i] += k * (x - 1);
}
}
int qry(bool f, int x) {
int ans = 0;
for (int i = x; i; i -= lb(i)) {
ans += (!f ? t1[i] : t2[i]);
}
return ans;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m;
For(i,1,n) {
cin >> a[i];
add(i, a[i] - a[i-1]);
}
while(m--) {
int op, x, y, k;
cin >> op >> x >> y;
if(op == 1) {
cin >> k;
add(x, k);
add(y+1, -k);
} else {
cout << (y * qry(0, y) - qry(1, y)) - (((x-1) * qry(0, x-1)) - qry(1, x-1)) << '\n';
}
}
return 0;
}
开两个树状数组分别维护 \(\sum\limits_{i=1}^xd_i\),\(\sum\limits_{i=1}^xd_i\times (i+1)\) 即可。
标签:ch,树状,int,sum,算法,数组,define From: https://www.cnblogs.com/Daniel-yao/p/17258699.html