标签:queue 第三十五 int max c++ 坐牢 stcak data size
一.作业
1.使用模版类自定义栈
代码:
#include <iostream>
using namespace std;
template<typename T>
// 封装一个栈
class stcak
{
private:
T *data; //
int max_size; // 最大容量
int top; // 下标
public:
// 无参构造函数
stcak();
// 有参构造函数
stcak(int size);
// 拷贝构造函数
stcak(const stcak &other);
// 析构函数
~stcak();
// 判空函数
bool empty();
// 判满函数
bool full();
// 扩容函数
void resize(int new_size);
// 返回元素个数函数
int size();
// 向栈顶插入元素函数
void push(T value);
// 删除栈顶元素函数
T pop();
// 访问栈顶元素函数
T get_top();
// 赋值重载函数
stcak &operator=(const stcak &other);
// 遍历栈里元素函数
void show();
//清空队列函数
void clear();
};
// 无参构造函数
template<typename T>
stcak<T>::stcak() : max_size(10)
{
data = new T[10];
max_size = 10;
top = -1;
cout << "无参构造" << endl;
}
// 有参构造函数
template<typename T>
stcak<T>::stcak(int size)
{
data = new T[size];
max_size = size;
top = -1;
cout << "有参构造" << endl;
}
// 拷贝构造函数
template<typename T>
stcak<T>::stcak(const stcak &other)
{
max_size = other.max_size;
top = other.top;
data = new T[max_size];
for (int i = 0; i <= top; i++)
{
data[i] = other.data[i];
}
cout << "拷贝构造" << endl;
}
// 析构函数
template<typename T>
stcak<T>::~stcak()
{
delete[] data;
cout << "析构函数" << endl;
}
// 判空函数
template<typename T>
bool stcak<T>::empty()
{
return top == -1;
}
// 判满函数
template<typename T>
bool stcak<T>::full()
{
return top == max_size - 1;
}
// 扩容函数
template<typename T>
void stcak<T>::resize(int new_size)
{
int *new_data = new T[new_size];
for (int i = 0; i <= top; i++)
{
new_data[i] = data[i];
}
delete[] data;
data = new_data;
max_size = new_size;
}
// 返回元素个数函数
template<typename T>
int stcak<T>::size()
{
return top + 1;
}
// 向栈顶插入元素函数
template<typename T>
void stcak<T>::push(T value)
{
if (full())
{
// 调用扩容函数
resize(max_size * 2);
}
data[++top] = value;
}
// 删除栈顶元素函数
template<typename T>
T stcak<T>::pop()
{
if (empty())
{
cout << "栈是空的";
return -1;
}
return data[top--]; // 出栈
}
// 访问栈顶元素函数
template<typename T>
T stcak<T>::get_top()
{
if (empty())
{
cout << "栈是空的";
return T();
}
return data[top];
}
// 赋值重载函数
template<typename T>
stcak<T> &stcak<T>::operator=(const stcak &other)
{
if (this == &other)
{
return *this;
}
delete[] data;
max_size = other.max_size;
top = other.top;
data = new T[max_size];
for (int i = 0; i <= top; i++)
{
data[i] = other.data[i];
}
return *this;
}
// 遍历栈里元素函数
template<typename T>
void stcak<T>::show()
{
if (empty())
{
cout << "遍历失败栈是空的"<<endl;
return;
}
cout << "栈里元素有:"<<endl;
for (int i = 0; i <= top; i++)
{
cout<< data[i] <<'\t';
}
cout <<endl;
}
//清空栈函数
template<typename T>
void stcak<T>::clear()
{
top=-1;
cout <<"栈已清空"<<endl;
}
/******************主函数*********************/
int main()
{
stcak<int> s;
s.push(1);
s.push(2);
s.push(3);
s.show();
cout << "栈的大小:" << s.size() << endl;
cout <<s.get_top()<< endl;
s.pop();
s.show();
cout << "栈的大小:" << s.size() << endl;
s.clear();
s.show();
return 0;
}
结果:

2.使用模版类自定义队列
代码:
#include <iostream>
using namespace std;
template<typename T>
class queue
{
private:
T *data; // 容器
int max_size; // 最大容量
int front; // 头下标
int tail; // 尾下标
public:
// 无参构造函数
queue();
// 有参构造函数
queue(int size);
// 拷贝构造函数
queue(const queue &other);
// 析构函数
~queue();
// 判空函数
bool empty();
// 判满函数
bool full();
// 扩容函数
void resize(int new_size);
// 元素个数函数
int size();
// 向队列尾部插入元素函数
void push(T value);
// 删除首个元素函数 出队
void pop();
// 遍历队列元素
void show();
// 赋值重载函数
queue &operator=(const queue &other);
//清空队列函数
void clear();
};
// 无参构造函数
template<typename T>
queue<T>::queue():max_size(10)
{
data = new T[10];
max_size = 10;
front = tail = 0;
cout << "无参构造" << endl;
}
// 有参构造函数
template<typename T>
queue<T>::queue(int size)
{
data = new T[size];
max_size = size;
front = tail = 0;
cout << "有参构造" << endl;
}
// 拷贝构造函数
template<typename T>
queue<T>::queue(const queue &other)
{
max_size=other.max_size;
front=other.front;
tail=other.tail;
data=new T[max_size];
for (int i = front; i != tail; i = (i + 1) % max_size)
{
data[i]=other.data[i];
}
cout << "拷贝构造" << endl;
}
// 析构函数
template<typename T>
queue<T>::~queue()
{
delete[] data;
cout << "析构函数" << endl;
}
// 判空函数
template<typename T>
bool queue<T>::empty()
{
return front == tail;
}
// 判满函数
template<typename T>
bool queue<T>::full()
{
return (tail+1)% max_size == front;
}
// 元素个数函数
template<typename T>
int queue<T>::size()
{
return (tail-front+max_size) % max_size;
}
// 扩容函数
template<typename T>
void queue<T>::resize(int new_size)
{
int *new_data = new T[new_size];
for (int i = front; i <= tail; i++)
{
new_data[i] = data[i];
}
data = new_data;
max_size = new_size;
front =0;
tail =size();
}
// 向队列尾部插入元素函数
template<typename T>
void queue<T>::push(T value)
{
if (full())
{
// 调用扩容函数
resize(max_size * 2);
}
data[tail] = value;
tail = (tail + 1) % max_size;
}
// 删除首个元素函数 出队
template<typename T>
void queue<T>::pop()
{
if (empty())
{
cout << "队列为空" << endl;
return ;
}
cout << data[front] << "出队" << endl;
front = (front + 1) % max_size;
// return 0;
}
// 遍历队列元素
template<typename T>
void queue<T>::show()
{
if (empty())
{
cout << "遍历失败队列为空" << endl;
return;
}
cout << "队列元素:" << endl;
for (int i = front; i != tail; i = (i + 1) % max_size)
{
cout << data[i] << '\t';
}
cout << endl;
}
// 赋值重载函数
template<typename T>
queue<T> &queue<T>::operator=(const queue &other)
{
if (this == &other)
{
return *this;
}
delete []data;
max_size=other.max_size;
front=other.front;
tail=other.tail;
data=new T[max_size];
for (int i = front; i != tail; i = (i + 1) % max_size)
{
data[i]=other.data[i];
}
cout << "拷贝赋值函数" <<endl;
return *this;
}
//清空队列函数
template<typename T>
void queue<T>::clear()
{
front=tail=0;
cout << "队列已清空"<<endl;
}
/******************主函数*********************/
int main()
{
queue<int> s;
s.push(1);
s.push(2);
s.push(3);
s.show();
cout << "队列的大小:" << s.size() << endl;
s.pop();
s.show();
cout << "队列的大小:" << s.size() << endl;
s.clear();
s.show();
return 0;
}
结果:
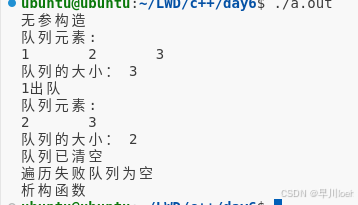
3.使用模版类自定义动态数组
代码:
#include <iostream>
#include <cstring> // 引入cstring以使用memcpy
using namespace std;
template <typename T>
class SeqList
{
private:
T *data; // 顺序表的数组
int max_size; // 容器最大内存
int size = 0; // 数组的大小
int len = 0; // 顺序表实际长度
public:
// 构造函数
SeqList()
{
init(10, 100);
}
SeqList(int s, int max_s)
{
init(s, max_s);
}
// 析构函数
~SeqList()
{
free();
}
// 拷贝构造
SeqList(const SeqList<T> &other)
{
init(other.size, other.max_size);
for (int i = 0; i < other.len; i++)
{
add(other.data[i]);
}
}
// 初始化函数
void init(int s, int max_s)
{
max_size = max_s;
size = s; // 当前数组的最大容量
data = new T[size]; // 在堆区申请一个顺序表容器
}
// 判空函数
bool empty()
{
return len == 0;
}
// 判满函数
bool full()
{
return size==len;
}
// 添加数据函数
bool add(T e)
{
if (data == NULL)
{
cout << "添加数据失败" << endl;
return false;
}
if (full())
{
if (len == max_size)
{
cout << "添加数据失败,内存已满" << endl;
return false;
}
expend();
}
data[len++] = e;
cout << "添加数据成功" << endl;
return true;
}
// 求当前顺序表的实际长度
int length()
{
return len;
}
// 任意位置插入函数
bool insert_pos(int pos, T e)
{
if (data == NULL || pos < 0 || pos > len)
{
cout << "插入数据失败" << endl;
return false;
}
if (full())
{
expend();
}
for (int i = len - 1; i >= pos; i--)
{
data[i + 1] = data[i];
}
data[pos] = e;
len++;
cout << "插入数据成功" << endl;
return true;
}
// 任意位置删除函数
bool delete_pos(int pos)
{
if (data == NULL || SeqList::empty() || pos < 0 || pos >= len)
{
cout << "删除数据失败" << endl;
return false;
}
for (int i = pos + 1; i < len; i++)
{
data[i - 1] = data[i];
}
len--;
cout << "删除数据成功" << endl;
return true;
}
// 访问容器中任意一个元素 at
T &at(int index)
{
if (data == NULL || SeqList::empty() || index < 0 || index >= len)
{
cout << "访问数据失败" << endl;
}
return data[index];
}
// 遍历整个数组输出
void show()
{
if (data == NULL || SeqList::empty())
{
cout << "遍历数组失败" << endl;
return;
}
cout << "数组中的数据:" << endl;
for (int i = 0; i < length(); i++)
{
cout << data[i] << '\t';
}
cout << endl;
}
// 君子函数:二倍扩容
void expend()
{
T *temp;
size = 2 * size;
temp = new T[size];
memcpy(temp, data, sizeof(T) * len);
free();
data = temp;
}
// 释放函数
void free()
{
delete[] data;
data = NULL;
cout << "释放空间成功" << endl;
}
};
int main()
{
SeqList<int> L;
L.add(1);
L.add(2);
L.add(3);
L.add(4);
L.add(5);
L.add(6);
L.add(6);
L.add(6);
L.add(99);
L.add(99);
L.add(99);
L.add(99);
L.show();
L.free();
L.show();
return 0;
}
结果:
二.思维导图
标签:queue,
第三十五,
int,
max,
c++,
坐牢,
stcak,
data,
size
From: https://blog.csdn.net/m0_62828714/article/details/141901816



