目录
前言
关于二叉树的存储,昨天我们提到有顺序存储和链式存储这两种方式,不过非完全二叉树顺序存储的话会造成很大的空间浪费,所以我们昨天使用的是链式存储结构。但是,对于二叉树的存储而言,引用(指针)是没办法存储到文件里的,也就没办法成功还原二叉树;此外,众所周知顺序表的查找是非常高效的,所以今天我们再次考虑二叉树的顺序存储。
一、压缩存储
对于非完全二叉树的顺序存储,我们昨天的方法是用特殊符号去填充“空位”,如下图:
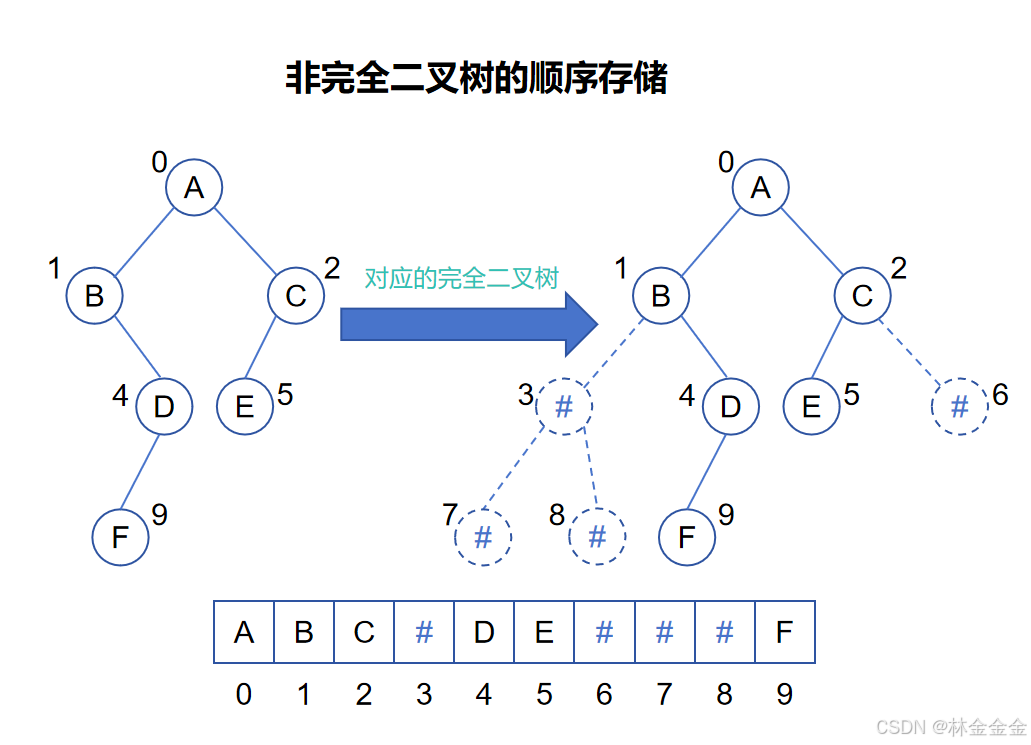
显然,这样确实会造成很大空间的浪费。所以,这里我们采取了“压缩存储”的方式对其改进优化,具体来说就是使用两个顺序表,一个顺序表存放每个有效结点的数据元素,另一个顺序表存放对应结点的索引值。改进后如下:
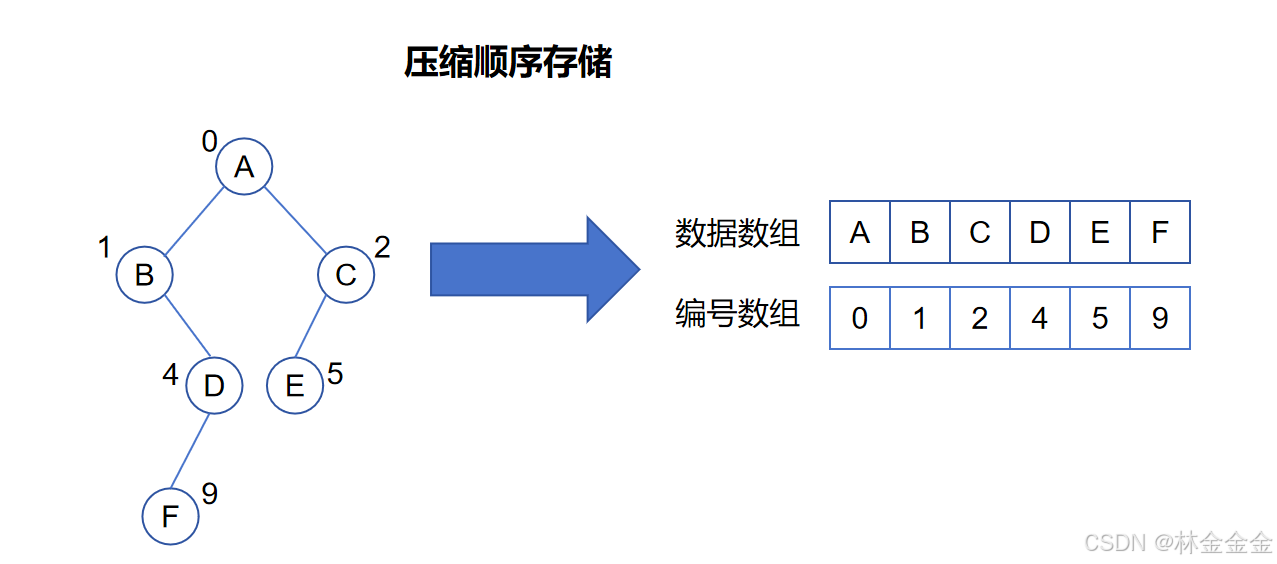
二、层次遍历
在昨天的文章中,如果仔细一点,其实可以发现,二叉树的顺序存储和层次遍历很相像,前者是从上往下、从左往右进行存储,而后者是从上往下、从左往右进行遍历,所以我们讨论二叉树的顺序存储,必然会用到层次遍历,也可以称为广度优先搜索(BFS:Breadth First Search)。
层次遍历要求从上往下、从左往右进行遍历,即需要确保在访问某个结点之前,该结点的所有前置结点(包括更高层次的结点以及同层次更左边的结点)都已经被访问,而队列“先进先出”的特性正好和该需求相吻合,能够实现层次遍历要求的从上往下、从左往右的访问顺序。因此,层次遍历基于队列实现。
以下图为例,在一个队列中,如果我们将D在B、C之后进入,那么D就会在B、C之后被访问;又将D在E、F、G之前入队,那么D就会在E、F、G之前被访问,这和层次遍历要求的从上往下、从左往右的顺序一模一样。
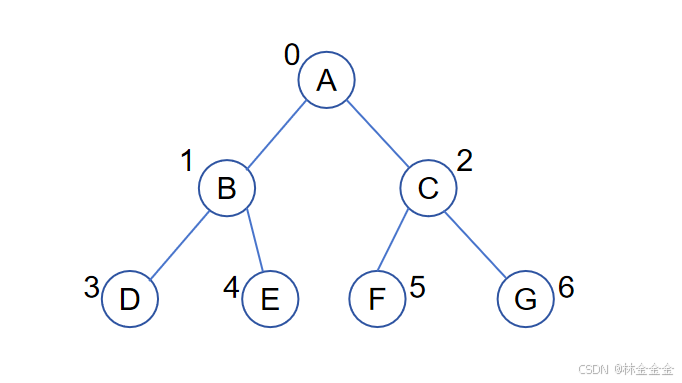
根据以上分析,层次遍历的具体过程可以总结如下:
- 创建一个队列,并将根结点入队
- 当队列不空时,取出队列中的第一个结点,访问该结点
- 将该结点的所有直接相连的子结点依次(从左往右)入队
- 又取出当前队列的第一个结点,访问该结点
- 将新取出结点的所有直接相连的子结点依次(从左往右)入队
- …………(不断重复以上操作,直到队列为空)
为方便理解,我们以上图为例,进行层次遍历:
- 创建一个队列,并将根结点A入队,此时队列变为[A]
- 显然队列不空,此时取出队列中的第一个结点(即结点A),访问结点A
- 将结点A的所有直接相连的子结点依次入队(即将结点B、C依次入队),此时队列变为[B,C]
- 显然队列不空,取出当前队列的第一个结点(即结点B),访问结点B
- 将结点B的所有直接相连的子结点依次入队(即将结点D、E依次入队),此时队列变为[C、D、E]
- 显然队列不空,取出当前队列的第一个结点(即结点C),访问结点C
- 将结点C的所有直接相连的子结点依次入队(即将结点F、G依次入队),此时队列变为[D、E、F、G]
- 显然队列不空,取出当前队列的第一个结点(即结点D),访问结点D
- D无子结点,不再入队,此时队列为[E、F、G]
- 显然队列不空,取出当前队列的第一个结点(即结点E),访问结点E
- E无子结点,不再入队,此时队列为[F、G]
- 显然队列不空,取出当前队列的第一个结点(即结点F),访问结点F
- F无子结点,不再入队,此时队列为[G]
- 显然队列不空,取出当前队列的第一个结点(即结点G),访问结点G
- 队列为空,遍历结束
为了后续操作方便,这里我们将队列代码再写一遍,不过需要把数据类型更改为Object型:
package datastructure.queue;
/**
* Circle Object queue.
*
* @author Xin Lin [email protected].
*/
public class CircleObjectQueue {
/**
* The total space. One space can never be used.
*/
public static final int TOTAL_SPACE = 10;
/**
* The data.
*/
Object[] data;
/**
* The index of the head.
*/
int head;
/**
* The index of the tail.
*/
int tail;
/**
*******************
* The constructor
*******************
*/
public CircleObjectQueue() {
data = new Object[TOTAL_SPACE];
head = 0;
tail = 0;
} // Of the first constructor
/**
*********************
* Enqueue.
*
* @param paraValue The value of the new node.
*********************
*/
public void enqueue(Object paraValue) {
if ((tail + 1) % TOTAL_SPACE == head) {
System.out.println("Queue full.");
return;
} // Of if
data[tail % TOTAL_SPACE] = paraValue;
tail++;
}// Of enqueue
/**
*********************
* Dequeue.
*
* @return The value at the head.
*********************
*/
public Object dequeue() {
if (head == tail) {
//System.out.println("No element in the queue");
return null;
} // Of if
Object resultValue = data[head % TOTAL_SPACE];
head++;
return resultValue;
} // Of dequeue
/**
*********************
* Overrides the method claimed in Object, the superclass of any class.
*********************
*/
public String toString() {
String resultString = "";
if (head == tail) {
return "empty";
} // Of if
for (int i = head; i < tail; i++) {
resultString += data[i % TOTAL_SPACE] + ", ";
} // Of for i
return resultString;
} // Of toString
/**
*********************
* The entrance of the program.
*
* @param args Not used now.
*********************
*/
public static void main(String args[]) {
CircleObjectQueue tempQueue = new CircleObjectQueue();
} // Of main
} // Of CircleObjectQueue补充以下3种基本数据类型:
- String:字符串
- boolean:布尔值
- Object:对象
三、代码实现
1.顺序表创建及初始化
首先,创建两个顺序表。由于今天的代码是基于昨天的代码,最后数据测试时使用的也是昨天创建的字符二叉树,所以这里我们定义数据数组时用char修饰(实际问题中,根据需要更改即可)。
/**
* The values of nodes according to breadth first traversal.
*/
char[] valuesArray;
/**
* The indices in the complete binary tree.
*/
int[] indicesArray;创建完毕后,进行初始化,由于后面我们数据测试时用的是昨天创建的二叉树,所以直接将该二叉树的结点总数作为顺序表的最大长度即可。
//Initialize arrays.
int tempLength = getNumNodes();
valuesArray = new char[tempLength];
indicesArray = new int[tempLength];
int i = 0;2.方法创建
首先,创建两个队列,一个数据队列,一个下标队列,并对这两个队列进行初始化,如下:
CircleObjectQueue tempQueue = new CircleObjectQueue();
tempQueue.enqueue(this);
CircleIntQueue tempIntQueue = new CircleIntQueue();
tempIntQueue.enqueue(0)对下标队列的初始化没什么好说的,就是将索引值0进行入队;而对数据队列的初始化,则是将this入队。这里需要简单补充一下this,this是指当前类的对象,和其他普通对象一样也可以通过点操作符来访问当前类的属性和方法,由于我们是在昨天代码的基础上进行,所以这里的当前类就是指昨天的BinaryCharTree类,因此this就是BinaryCharTree类的一个对象,即一个结点。这里初始化数据队列时将this入队,就相当于把this作为了根结点。
根据上面我们对层次遍历具体过程的总结,代码模拟如下:
BinaryCharTree tempTree = (BinaryCharTree) tempQueue.dequeue();
int tempIndex = tempIntQueue.dequeue();
while (tempTree != null) {
valuesArray[i] = tempTree.value;
indicesArray[i] = tempIndex;
i++;
if (tempTree.leftChild != null) {
tempQueue.enqueue(tempTree.leftChild);
tempIntQueue.enqueue(tempIndex * 2 + 1);
} // Of if
if (tempTree.rightChild != null) {
tempQueue.enqueue(tempTree.rightChild);
tempIntQueue.enqueue(tempIndex * 2 + 2);
} // Of if
tempTree = (BinaryCharTree) tempQueue.dequeue();
tempIndex = tempIntQueue.dequeue();
} // Of while因为创建队列及根结点入队之前就已经完成了,所以这里直接从取出队列的第一个结点开始,需要注意,由于我们创建的数据队列是Object类型,所以出队时需要“强转”一下,变成BinaryCharTree类型。
然后将该取出结点进行存储,即把数据域(即tempTree.value)赋给数据数组valuesArrays[i],把对应下标(即tempIndex)赋给下标数组indicesArrays[i]。
如果该取出结点的左子树不空,则将它的左子树入队(数据队列),同时将tempIndex * 2 + 1入队(下标队列),右子树同理。然后,再次取出当前数据队列的第一个结点赋给tempTree,同时取出下标队列中的对应下标赋给tempIndex。
3.数据测试
接下来,我们利用昨天创建的二叉树进行数据测试,最后输出时调用Arrays类中的toString()方法,以便输出一维数组的字符串形式,代码如下:
/**
*********************
* The entrance of the program.
*
* @param args Not used now.
*********************
*/
public static void main(String args[]) {
BinaryCharTree tempTree = manualConstructTree();
System.out.println("\r\nPreorder visit:");
tempTree.preOrderVisit();
System.out.println("\r\nIn-order visit:");
tempTree.inOrderVisit();
System.out.println("\r\nPost-order visit:");
tempTree.postOrderVisit();
System.out.println("\r\n\r\nThe depth is: " + tempTree.getDepth());
System.out.println("The number of nodes is: " + tempTree.getNumNodes());
tempTree.toDataArrays();
System.out.println("The values are: " + Arrays.toString(tempTree.valuesArray));
System.out.println("The indices are: " + Arrays.toString(tempTree.indicesArray));
}// Of main 4.完整的程序代码
package datastructure.tree;
import datastructure.queue.*;
import java.util.Arrays;
/**
* Binary tree with char type elements.
*
*@auther Xin Lin [email protected].
*/
public class BinaryCharTree {
/**
* The value
*/
char value;
/**
* The left child
*/
BinaryCharTree leftChild;
/**
* The right child
*/
BinaryCharTree rightChild;
/**
*********************
* The first constructor.
*
* @param paraName The value.
*********************
*/
public BinaryCharTree(char paraName) {
value = paraName;
leftChild = null;
rightChild = null;
} // of constructor
/**
*********************
* Manually construct a tree. Only for testing.
*********************
*/
public static BinaryCharTree manualConstructTree() {
// Step 1. Construct a tree with only one node.
BinaryCharTree resultTree = new BinaryCharTree('a');
// Step 2. Construct all Nodes. The first node is the root.
// BinaryCharTree tempTreeA = resultTree.root;
BinaryCharTree tempTreeB = new BinaryCharTree('b');
BinaryCharTree tempTreeC = new BinaryCharTree('c');
BinaryCharTree tempTreeD = new BinaryCharTree('d');
BinaryCharTree tempTreeE = new BinaryCharTree('e');
BinaryCharTree tempTreeF = new BinaryCharTree('f');
BinaryCharTree tempTreeG = new BinaryCharTree('g');
// Step 3. Link all Nodes.
resultTree.leftChild = tempTreeB;
resultTree.rightChild = tempTreeC;
tempTreeB.rightChild = tempTreeD;
tempTreeC.leftChild = tempTreeE;
tempTreeD.leftChild = tempTreeF;
tempTreeD.rightChild = tempTreeG;
return resultTree;
} // of manualConstructTree
/**
*********************
* Pre-order visit.
*********************
*/
public void preOrderVisit() {
System.out.print("" + value + " ");
if(leftChild != null) {
leftChild.preOrderVisit();
} // of if
if(rightChild != null) {
rightChild.preOrderVisit();
} // of if
} // of preOrderVisit
/**
*********************
* In-order visit.
*********************
*/
public void inOrderVisit() {
if(leftChild != null) {
leftChild.inOrderVisit();
} // of if
System.out.print("" + value + " ");
if(rightChild != null) {
rightChild.inOrderVisit();
} // of if
} // of inOrderVisit
/**
*********************
* Post-order visit.
*********************
*/
public void postOrderVisit() {
if(leftChild != null) {
leftChild.postOrderVisit();
} // of if
if(rightChild != null) {
rightChild.postOrderVisit();
} // of if
System.out.print("" + value + " ");
} // of postOrderVisit
/**
*********************
* Get the depth of the binary char tree.
*
* @return The depth.
*********************
*/
public int getDepth() {
if((leftChild == null) && (rightChild == null)) {
return 1;
} // of if
// The depth of the left child.
int tempLeftDepth = 0;
if(leftChild != null) {
tempLeftDepth = leftChild.getDepth();
} // of if
// The depth of the right child.
int tempRightDepth = 0;
if(rightChild != null) {
tempRightDepth = rightChild.getDepth();
} // of if
if(tempLeftDepth >= tempRightDepth) {
return tempLeftDepth + 1;
} else {
return tempRightDepth + 1;
} // of if
} // of getDepth
/**
*********************
* Get the number of nodes of the binary char tree.
*
* @return The number of nodes.
*********************
*/
public int getNumNodes() {
if((leftChild == null) && (rightChild == null)) {
return 1;
} // of if
// The number of nodes of the left child.
int tempLeftNodes = 0;
if(leftChild != null) {
tempLeftNodes = leftChild.getNumNodes();
} // of if
// The number of nodes of the right child.
int tempRightNodes = 0;
if(rightChild != null) {
tempRightNodes = rightChild.getNumNodes();
} // of if
// The total number of nodes.
return tempLeftNodes + tempRightNodes + 1;
} // of getNumNodes
/**
* The values of nodes according to breadth first traversal.
*/
char[] valuesArray;
/**
* The indices in the complete binary tree.
*/
int[] indicesArray;
/**
********************
* Convert the tree to data arrays, including a char array and an int array.
* The results are stored in two member variables.
*
* @see #valuesArray
* @see #indicesArray
*********************
*/
public void toDataArrays() {
//Initialize arrays.
int tempLength = getNumNodes();
valuesArray = new char[tempLength];
indicesArray = new int[tempLength];
int i = 0;
//Traverse and convert at the same time.
CircleObjectQueue tempQueue = new CircleObjectQueue();
tempQueue.enqueue(this);
CircleIntQueue tempIntQueue = new CircleIntQueue();
tempIntQueue.enqueue(0);
BinaryCharTree tempTree = (BinaryCharTree) tempQueue.dequeue();
int tempIndex = tempIntQueue.dequeue();
while (tempTree != null) {
valuesArray[i] = tempTree.value;
indicesArray[i] = tempIndex;
i++;
if (tempTree.leftChild != null) {
tempQueue.enqueue(tempTree.leftChild);
tempIntQueue.enqueue(tempIndex * 2 + 1);
} // Of if
if (tempTree.rightChild != null) {
tempQueue.enqueue(tempTree.rightChild);
tempIntQueue.enqueue(tempIndex * 2 + 2);
} // Of if
tempTree = (BinaryCharTree) tempQueue.dequeue();
tempIndex = tempIntQueue.dequeue();
} // Of while
} // Of toDataArrays
/**
*********************
* The entrance of the program.
*
* @param args Not used now.
*********************
*/
public static void main(String args[]) {
BinaryCharTree tempTree = manualConstructTree();
System.out.println("\r\nPreorder visit:");
tempTree.preOrderVisit();
System.out.println("\r\nIn-order visit:");
tempTree.inOrderVisit();
System.out.println("\r\nPost-order visit:");
tempTree.postOrderVisit();
System.out.println("\r\n\r\nThe depth is: " + tempTree.getDepth());
System.out.println("The number of nodes is: " + tempTree.getNumNodes());
tempTree.toDataArrays();
System.out.println("The values are: " + Arrays.toString(tempTree.valuesArray));
System.out.println("The indices are: " + Arrays.toString(tempTree.indicesArray));
}// Of main
} // of class BinaryCharTree注意,由于在创建队列时我们用到了CircleObjectQueue类(位于datastructure.queue包),而在数据测试时使用了Arrays类中的toString()方法,所以在程序开头需要进行导包。其中*为import通配符,表示导入指定包里的所有类。
import datastructure.queue.*; import java.util.Arrays;
运行结果:

总结
今天我们主要涉及的是二叉树的层次遍历以及“压缩顺序存储”。层次遍历从根结点开始,逐层向下进行遍历访问,这种遍历方式能够保证树的每一个结点都被访问到,且只被访问一次;同时,层次遍历这种从上往下、从左往右的有序性在很多场景中都是必需的,比如树的序列化、重建。为了实现二叉树的“压缩顺序存储”,我们采用的是层次遍历与队列结合使用。尽管树的链式存储结构操作简便,但我们仍然考虑使用顺序存储,这说明在选择数据结构时,我们除了需要考虑操作的便利性,还需要考虑到表示是否优良。
标签:BinaryCharTree,结点,Java,队列,day22,入队,二叉树,tempTree,null From: https://blog.csdn.net/2301_80594618/article/details/141172896