目录
1 概述
位置一分配问题起源于美国民用航空局(CAB),其航空公司航线的结构为轴辐系统(Hub-and-Spoke),以某一个主要的机场为轴(Hub),众多由此辐射而出的航线为辐(Spoke),在中枢的主要机场看成一个转运点,从而提供旅客和货物的转运.其中 P-Hub中心问题即是轴辐系统的一种,该问题已广泛应用在现实生活中,如航线问题、邮件传送问题、货物运送问题、通讯问题等.
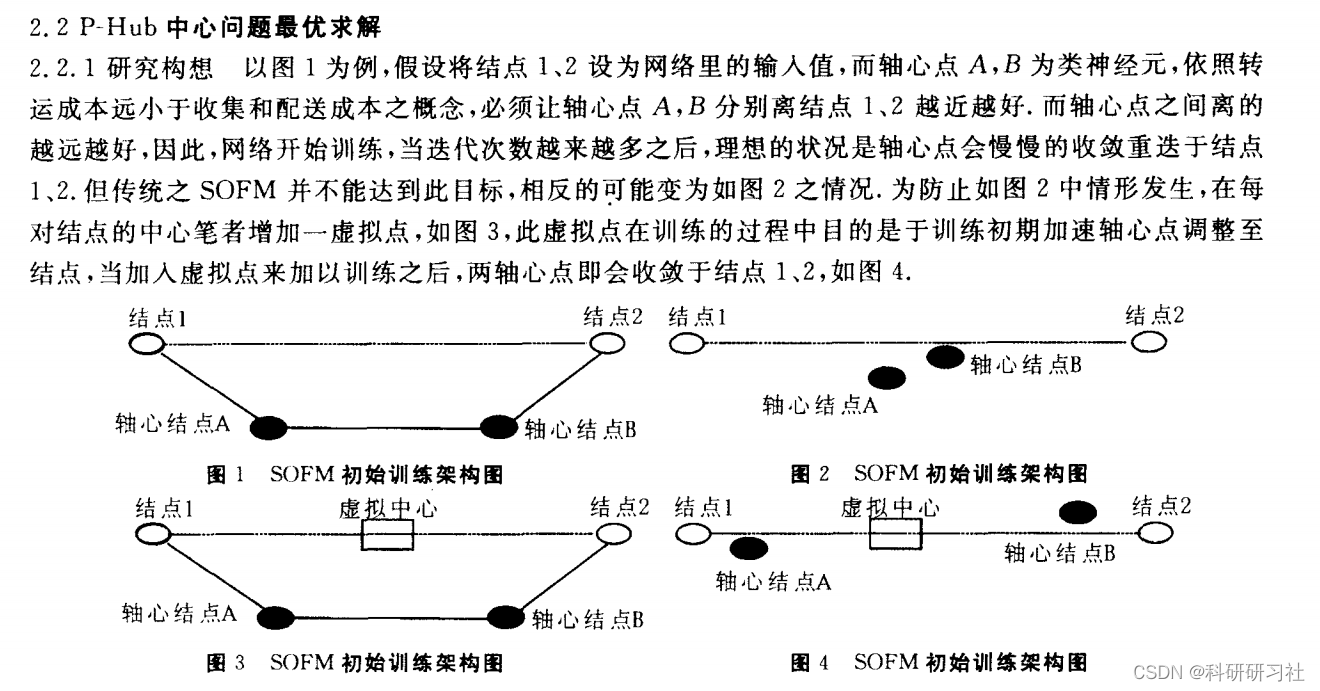
基于粒子群优化(Particle Swarm Optimization, PSO)算法的p-Hub选址问题是一个在物流、交通、网络设计等领域中常见的组合优化问题。该问题旨在从众多候选地点中选择p个hub(中心节点),以最小化整个网络中的运输成本或最大化网络效率。Hub是网络中的关键节点,用于集中和分配流量,而p-Hub问题则是确定最优的hub数量和位置,使得通过这些hub的货物或信息流通达到最优化。
p-Hub 选址问题概述
在p-Hub问题中,通常有一个完整的无向图G=(V,E),其中V是节点集合,表示可能的地点;E是边集合,表示两地点之间的直接连接及其关联成本。目标是选择一个由p个节点组成的子集H⊆V作为hub,所有非hub节点到其最近hub的总距离(或成本)被最小化。这涉及到解决两个子问题:一是决定哪些节点成为hub,二是如何有效地将非hub节点分配给这些hub。
粒子群优化算法简介
粒子群优化算法是一种基于群体智能的全局优化技术,灵感来源于鸟群觅食行为。在PSO中,每个解表示为一个“粒子”,在解空间中飞行并更新其位置以接近最优解。每个粒子有两个关键参数:位置(代表潜在解决方案)和速度(指导位置的更新)。通过迭代地调整这些粒子的位置和速度,算法逐渐搜索到问题的最优或近似最优解。
PSO应用于p-Hub选址问题
应用PSO解决p-Hub问题时,每个粒子代表一个潜在的hub配置(即p个hub的位置选择)。粒子的位置可以通过编码来表示,例如使用二进制或实数编码。适应度函数评估每个配置的整体成本,即所有非hub节点到其最近hub的距离之和。PSO算法的更新规则会驱动粒子群探索解空间,通过个体最优解(pBest)和全局最优解(gBest)来引导搜索方向,逐渐逼近最优的hub布局。
关键步骤
- 初始化:随机生成初始粒子群,每个粒子代表一个hub配置。
- 评估:计算每个粒子的适应度值(即总成本)。
- 更新速度与位置:根据当前速度、个体最优解和全局最优解更新每个粒子的速度和位置。
- 重复评估与更新:进行多次迭代,直到满足停止条件(如达到最大迭代次数或适应度改进小于预定阈值)。
- 结果输出:输出找到的最佳hub配置及其相应的总成本。
挑战与改进
- 早熟收敛:PSO容易在局部最优解附近过早收敛。为克服此挑战,可以引入多样性保持机制,如动态调整惯性权重、采用多群策略或引入自适应变异操作。
- 大规模问题处理:对于大规模网络,PSO的计算复杂度较高。采用启发式初始化、并行处理或与局部搜索算法结合可提高效率。
基于粒子群优化的p-Hub选址优化研究是一个不断发展的领域,通过算法的持续改进和针对特定问题的定制化,能更有效地解决实际的网络设计和物流规划问题。
部分代码:
function sol=ParseSolution(xhat,model)
N=model.N;
P=model.P;
c=model.c;
alpha=model.alpha;
f=model.f;
r=model.r;
xii=diag(xhat)';
if any(xii>=0.5)
[~, so]=sort(xii,'descend');
nHub=0;
for i=so
if xii(i)<0.5 || nHub>=P
break;
end
xii(i)=1;
nHub=nHub+1;
end
xii(xii<1)=0;
else
[~, imax]=max(xii);
xii(:)=0;
xii(imax)=1;
end
Hubs=find(xii==1);
x=xhat;
for i=1:N
if xii(i)==0
x(i,:)=0;
else
x(:,i)=0;
x(i,i)=1;
end
end
h=zeros(1,N);
for i=1:N
XI=x(:,i);
XI(xii==0)=-inf;
[~, h(i)]=max(XI);
x(:,i)=0;
x(h(i),i)=1;
end
oc=zeros(N,N);
for i=1:N
for j=1:N
if i==j
oc(i,j)=0;
else
k=h(i);
l=h(j);
oc(i,j)=c(i,k)+alpha*c(k,l)+c(l,j);
end
end
end
ocr=oc.*r;
SumOCR=sum(ocr(:));
xiif=xii.*f;
SumXF=sum(xiif);
TotalCost=SumOCR+SumXF;
sol.x=x;
sol.h=h;
sol.Hubs=Hubs;
sol.SumOCR=SumOCR;
sol.SumXF=SumXF;
sol.TotalCost=TotalCost;
end
2 运行结果
2.1 算例1


2.2 算例2

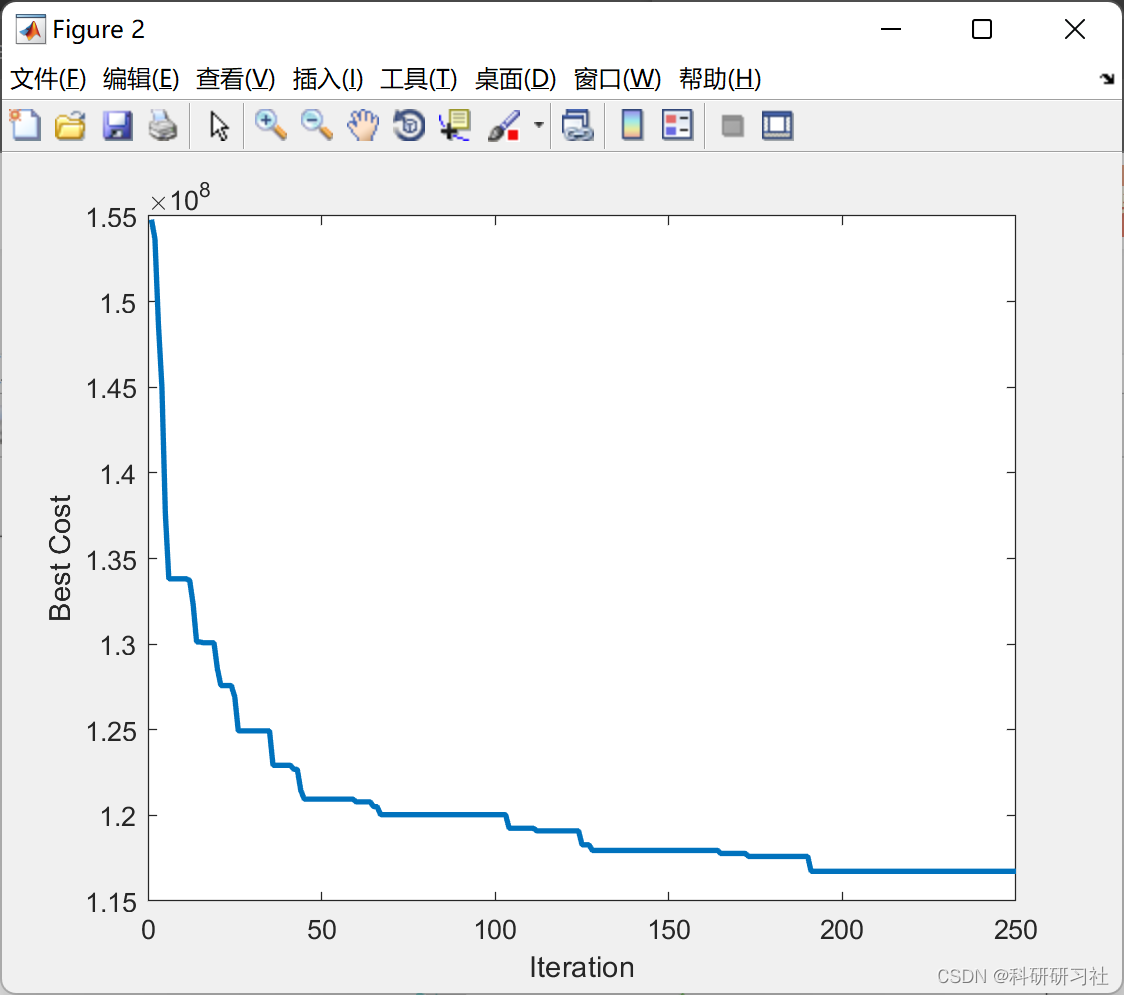
2.3 算例3
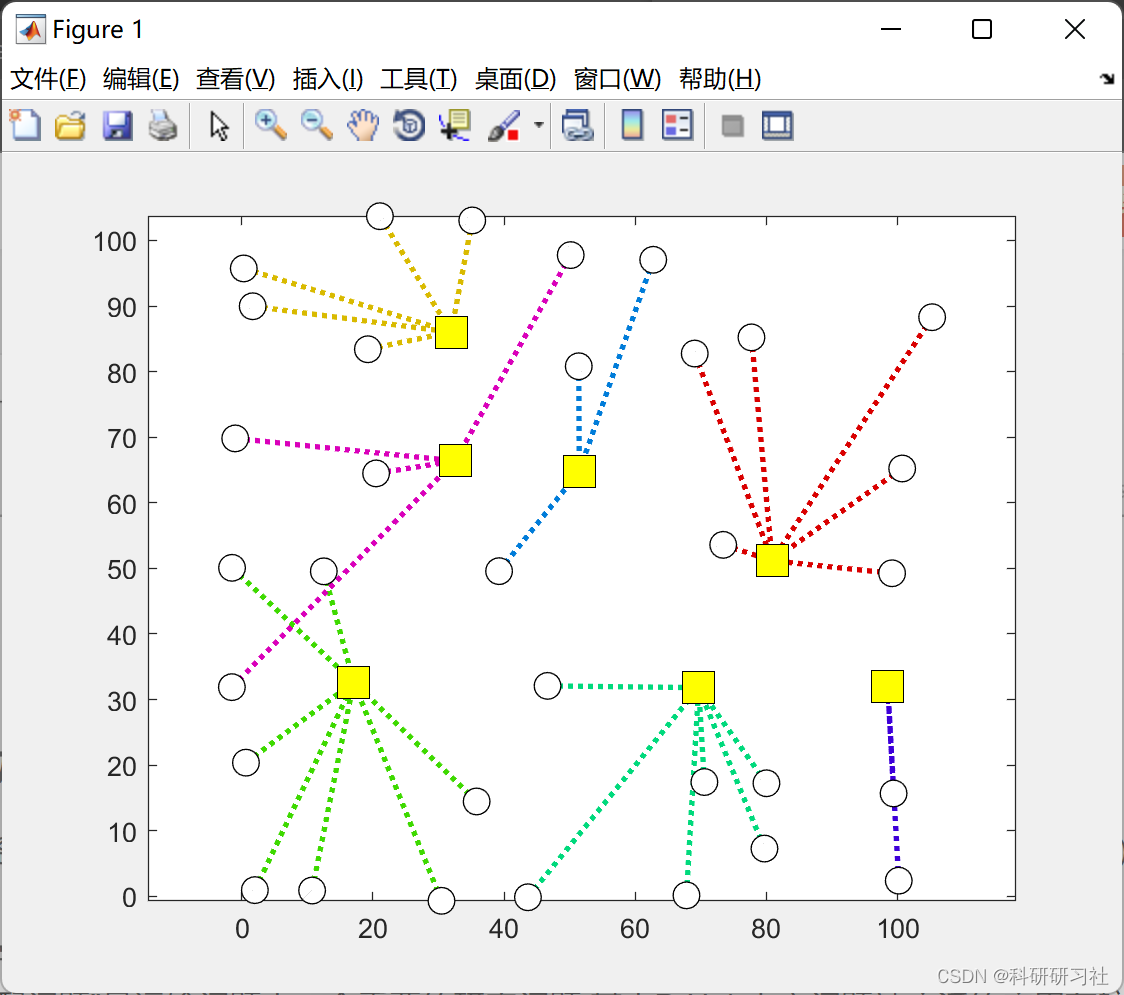

3 参考文献
部分理论引用网络文献,如有侵权请联系删除。
[1]卓月明,樊晓兵.基于SOFM的P-Hub中心问题的最优求解.吉首大学学报:自然科学版,2009(5):60-63
机构:吉首大学物理科学与信息工程学院
摘要:"位置-分配问题"是运输问题中一个重要的研究问题,其中P-Hub中心问题被广泛的应用在航空、通讯、邮件送发问题上.目前已有许多启发式的方法被广泛应用求最优解,如基因算法、模拟退火法、Hopfield network等;本研究针对顾客及服务中心数目已知的条件下,提出了基于人工神经网络的自组织特征映射网络求解方法,运用神经元的自我学习功能来找出最佳的服务中心位置.