前言:
此文章为线段树基础知识可供学习参考
咳咳,进入正题:
我们在做题的时候可能会遇到 给定一个数组 同时给出一个值进行修改 或是 区间性的操作
这里以单点修改和区间查询为例子:
我们每次枚举一遍答案可能会非常的慢,时间分别可能为 \(O(1)\), \(O(n)\)
或许会有人说 用前缀和 区间求和就会降为 \(O(1)\) 但是区间求改 变为了\(O(n)\) 那有没有可能平均一下 将两个情况都成 \(O(\log n)\)
答案肯定是有的 : 那就是线段树———— Segment tree。
线段树学习分为 \(3\) 个阶段 --------- 自我总结 \(4\) 个知识点如下:
(我会根据以下的顺序进行续写)
1.1: 建树;
2.1: 单点修改;
2.1.1: 单点增值
3.1: 区间修改;
3.1.1: 区间求和;
3.1.2: 区间增值;
3.1.3: 区间查询
4.1 : lazy标记 *
1.1: 建树:
对于线段树的编写 第一步的重点就是建树 此后所有进行的更改均需第一步建树
顾名思义: 建树从字面意义上来讲就是 数组以树的方式存储下来。
举个例子:
令 \(a_{n} = \left\{1,3,5,7,9,11\right\}\)
同时再开一个数组 \(tree[4 \cdot n]\) (这里对于线段树来说一般需要开 \(4 \cdot n\) 的空间 \(n\) 为原数组大小)
核心思想:每次进行对数组二分 分为 L R 两个分叉 每个叶子的父节点为其子节点的和
下面我将以图的形式把 \(a\) 数组所对应的 \(tree\) 展现出来 方便理解;
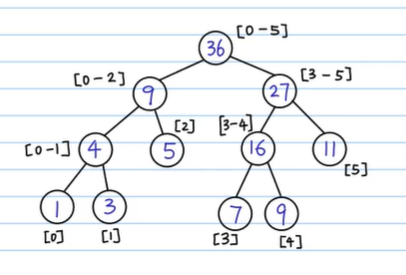
P.s.图为b站某up主的,仅为参考
此图即为 \(a\) 数组所对应的 \(tree\) 在这颗树上每个父节点即为其右上角所对应的区间和
相应代码如下:
void build_tree(int node, int start, int end)//node为本节点
{
if (start == end)//start为区间的左端 , end即为右端
tree[node] = arr[start];//如果start == end 说明已经遍历到本棵树的最深节点 我们就将其存储下来
else
{
int mid = (start + end) / 2;//每次将其二分
int left_node = 2 * node + 1;//这里对应着其节点的左儿子
int right_node = 2 * node + 2;//则这里为右儿子
build_tree(left_node, start, mid);
build_tree(right_node, mid + 1, end);//递归进行求解
tree[node] = tree[left_node] + tree[right_node];//这里说明本node的节点为其左右儿子的和
}
}
最后,我们只需按照 层序遍历 将其输出, 答案即为 \(a\) 数组 的 树 组:
a数组 1 3 5 7 9 11
对应下标: 0 1 2 3 4 5
tree数组 36 9 27 4 5 16 11 1 3 0 0 7 9 0 0
对应下标 : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
(正常来说可能会出现非满二叉树的情况我们只需要 其余空节点记为 \(0\) 即可方便查询)
以上为建树的所有内容。
2.1 单点修改
单点修改分为:
1.单点更改。
2.单点增值。
什么是单点更改呢? 举个栗子:
给出一组数 1 3 5 7 9 11
下标 0 1 2 3 4 5
请将下标为 3 的数 变为 9
这里输出的是: 1 3 5 9 9 11
根据常理来说 从头开始遍历 一个一个枚举 时间复杂度为 O(n)。
若有时可以为 O(1) 的情况 不过出题人不会那么良心的。
因此 我们需要加速 便可以用线段树来做。
大体的思路 : 从最高父节点遍历 通过给定的下标确定数所在的区间 进行深层搜索 直到找到为止)。
我们还是以图的形式论述,更加直观:
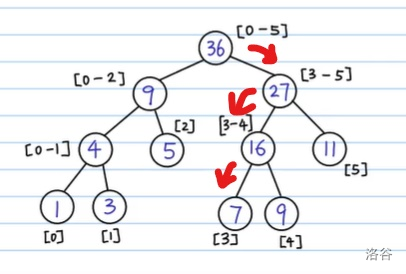
对于 \(3\) 这个下标 首先找到对应区间 发现 :
\(2 < 3 < 5\) 。
所以 区间便到了 \([ 3 \sim 5 ]\)。
此时我们可以发现 继续往下搜索 通过比对 :
$ 3 < 4 < 5$。
因此 区间便到了 \([ 3 \sim 4 ]\)。
发现依然没有找到答案 所以继续往下;直到节点 \([ 3 ]\) 停止搜索 将其数值更新 。
可是更新之后 此棵树的左半部分所有父节点收到了影响 违背了线段树的原理:
每个叶子的父节点为其子节点的和。
所有 最后我们还需自下而上进行更新节点操作。
代码如下:
void arr_tree(int node, int start, int end, int X, int K)//将 X 的值变为 K
{
if (start == end)//如果找到
{
arr[X] = K;//更新原数组
tree[node] = arr[X];同时更新树
}
else
{
int mid = (start + end) / 2;
int left_node = 2 * node + 1;
int right_node = 2 * node + 2;
if (X >= start && X <= mid)//如果 X 比中值小则遍历左区间
arr_tree(left_node, start, mid, X, K);
else //反之则遍历右区间
arr_tree(right_node, mid + 1, end, X, K);
tree[node] = tree[left_node] + tree[right_node];//更新每个更改后的父节点
}
}
以上则为单点修改所有内容。
2.1.1 单点增值
这里 单点增值 指的是给定一个下标 使该下标上的数增加 \(n\)。
其实原理单点修改完全一样 不多论述,将其代码改一处地方即可:
if (start == end)
{
arr[X] += K;
tree[node] += K;
}
P.s: 每一次增值后需将 \(lazy\) 下放 ( \(lazy\) 数组具体后面说
2.1 整节 结束
3.1 区间性问题
3.1.1 : 区间求和
大意为 :给定一个左端点 给定一个右端点 求得左右端点之间所有数的和。
继续接着线段树的思路说 :
在建完树之后 我们可以得知 父节点即为 --- 左儿子 \(+\) 右儿子
因此只需要判断一下 \(\text{L}\), \(\text{R}\) 所包含的区间在哪即可 从最底层遍历 直到 $start = L $, \(end = R\)
代码如下:
int query_tree(int node, int start, int end, int L, int R)
{
if (R < start || L > end)//若区间不覆盖此数组之间返回0
return 0;
else if (L <= start && end <= R)//剪枝
return tree[node];
else if (start == end)
return tree[node];//若遍历到最深节同样返回值
else
{
int mid = (start + end) / 2;
int left_node = 2 * node + 1;
int right_node = 2 * node + 2;
int sum_left = query_tree(left_node, start, mid, L, R);
int sum_right = query_tree(right_node, mid + 1, end, L, R);//分别遍历左右子树 进行求和
return sum_left + sum_right;//返回左右子树相加结果
}
}
3.1.2: 区间增值 ( 雾
意义: 给定 \(\text{L}\), \(\text{R}\) 将其所有值相加。
如果按照线段树进行之间修改 时间复杂度会飞起QAQ
所以,这里提前引入一个新东西 : lazy标记。
\(lazy\) 标记顾名思义:懒标记..
思路 : 在每次遍历子树时 若找到 \(\text{L}\), \(\text{R}\) 所在的区间 则在当前父节点打上标记 将其值更新为:$val + val \cdot up $ 即为更新后的值。 每次遍历时将标记下放 , 取消先前标记 以后遍历时标记过的点直接跳过即可 直至更新的最深层节点。
这样子操作之后 大大降低了时间复杂度。
代码如下:
void push_down(int node, int m)
{
if (add[node])
{
add[2 * node + 1] += add[node];
add[2 * node + 2] += add[node];
tree[2 * node + 1] += (m - (m >> 1)) * add[node];
tree[2 * node + 2] += (m >> 1) * add[node];
add[node] = 0;
}
}
这里 \(add\) 为 \(lazy\) 数组 这里包含了下放操作 由此可知没此更新 \(lazy\) 数组之后 重新赋值为 \(0\) (删除标记)
$ m $ 为此修改区间长度
3.1.2: 区间增值
讲完了 \(lazy\) 数组之后其实区间增值就很好理解了。
和区间求和一样 分左右子树根据区间进行遍历 每一次递归后再更新其父节点的值
代码如下:
void arr_tree(int node, int start, int end, int L, int R)
{
if (L <= start && end <= R)
{
add[node] += 1;
tree[node] = end - start + 1 - tree[node];
return;
}
push_down(node, end - start + 1);
//本节点进行标记 并且做下放操作 长度即为 end - start + 1
int mid = (start + end) / 2;
int left_node = 2 * node + 1;
int right_node = 2 * node + 2;
if (L <= mid)
arr_tree(left_node, start, mid, L, R);
if (R > mid)
arr_tree(right_node, mid + 1, end, L, R);
tree[node] = tree[left_node] + tree[right_node];//更新节点
}
这里代码给出的是 将 \(L \sim R\) 这个区间所有数加一 ( 非常容易理解是不是qwq
3.1.3: 区间查询
我想 看到这里 大家对线段树已经 有了很深的理解了 区间查询我就不多说了 和所有区间操作一样。
口糊一下思路: 遍历子树 直到相对应的节点 输出即可 若直接有树上修改操作 则每次遍历需 pushdown 。
好啦 线段树的学习就到这了 以上所有的乘除操作均可以换成位运算加快效率
最后给出一个洛谷官方的 线段树练习题单:
标签:node,int,线段,tree,笔记,start,算法,区间,节点 From: https://www.cnblogs.com/S1gMa/p/16808365.html