首先区别一下图跟树:
树不会包含环,图可以包含环。
图的生成树其实就是在图中找一棵包含图中的所有节点的树。专业点说,生成树是含有图中所有顶点的无环连通子图。
最小生成树就是再所有可能的生成树中,权重和最小的那棵生成树就叫最小生成树(注意:最小生成树有n-1条边)。
Kruskal算法和Prim算法都是用于解决图的最小生成树(Minimum Spanning Tree,简称MST)问题的经典算法。在这个问题中,我们需要找到一个图中的最小生成树,即包含所有节点但总权重最小的子图(B站有up主做了很易懂的动画:【最小生成树(Kruskal(克鲁斯卡尔)和Prim(普里姆))算法动画演示】https://www.bilibili.com/video/BV1Eb41177d1?vd_source=dd65e5938f5f6dab5dc478dad590c5f9)。
Kruskal算法:
1. 概述:
Kruskal算法是一种贪婪算法,它通过不断选择边来构建最小生成树。它的基本思想是从小到大选择图中的边,并且保证所选边不构成环。
2. 算法步骤:
- 初始化: 将所有的边按照权重从小到大进行排序。
- 循环选择边: 从最小的边开始,依次考虑每一条边。
- 如果当前边不会形成环(即加入该边后不会导致图中出现环),则选择该边加入最小生成树。
- 如果形成环,则舍弃该边。
- 重复步骤直至生成树包含了所有的节点。
 图片来自b站up主@WAY_zhong
图片来自b站up主@WAY_zhong
3. 实现要点:
- 使用并查集来判断是否形成环。
Prim算法:
1. 概述:
Prim算法也是一种贪婪算法,它从一个节点开始逐步构建最小生成树。与Kruskal算法不同,Prim算法是基于节点而不是边的选择来构建最小生成树。
2. 算法步骤:
- 选择初始节点: 从图中任意一个节点开始。
- 逐步扩展生成树:
- 在当前的最小生成树集合和其余节点中选择一个最小权重的边,将其加入最小生成树。
- 将新加入的节点加入到最小生成树的集合中。
- 重复步骤直至生成树包含了所有的节点。
 图片来自b站up主@WAY_zhong
图片来自b站up主@WAY_zhong
3. 实现要点:
- 使用优先队列来选择最小权重的边。
- 用一个集合来记录已经加入最小生成树的节点,以避免重复选择。
例题引入
leetcode 第1584题 https://leetcode.cn/problems/min-cost-to-connect-all-points/description/
题目:给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的 曼哈顿距离 :|xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
示例 1:
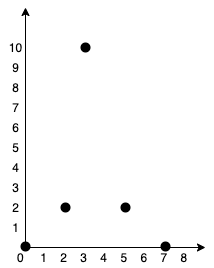
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出:20
解释:
我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达
Kruskal算法
思路:
- 首先,遍历点集points,构建边,并将该边在points中的下标i,j和曼哈顿距离d存入arr
- 由于Kruskal特点是先添加费用小的边,所以将arr按照曼哈顿距离从小到大排序
- 利用并查集构建最小生成树。如果当前边的两个点没有不在最小生成树中,则将该边添加到最小生成树中,更新边数和费用,edge+=1,cost+=d,当边数edge==n-1时,说明构建完最小生成树。
点击查看代码
class Solution:
def minCostConnectPoints(self, points: List[List[int]]) -> int:
res = [] #存储每条边在points中的两个下标和曼哈顿距离
n = len(points)
# 计算任意两点之间的曼哈顿距离,并将边添加到边列表中
for i in range(n):
x1, y1 = points[i]
for j in range(i+1,n):
x2,y2 = points[j]
res.append([i,j,abs(x2-x1)+abs(y2-y1)]) #i,j表示边的起点和终点
#对边排序
res.sort(key=lambda x:x[2])
#初始化并查集
parent = list(range(n))#列表存储了每个节点的父节点信息。
#在最初的时候,每个节点的父节点都是自身,即parent[i] = i,表示每个节点自成一个集合。
def find(x):
if x != parent[x]:
parent[x] = find(parent[x])
return parent[x]
#构建最小生成树
edge = 0 #初始化边数为0
cost = 0
for i ,j ,d in res:
a,b = find(i),find(j)
if a!= b: #每次考虑一条边,检查该边的两个端点是否已经在同一个集合中(即是否构成环)
parent[b] = a
edge += 1
cost += d
if edge == n-1: #结束条件(最小生成树边数为n-1)
break
return cost
Prim算法
思路:
初始化:
- d列表用于表示各个顶点与加入最小生成树的顶点之间的最小距离,初始值设为无穷大。
- vis列表表示是否已经加入到了最小生成树中,初始值设为False。
选择初始点:
- 选取第一个点作为起始点,将其距离设为0,表示到自身的距离为0。
逐步扩展生成树:
- 外层循环迭代每个点
- 内层循环在未加入最小生成树的点中找到距离最小的点。
- 将找到的点加入最小生成树,并更新距离列表。
- 计算当前轮的最小距离,并加入到答案中。
返回结果:
- 返回连接所有点的最小总费用ans。
点击查看代码
n = len(points)
d = [float("inf")]*n # 表示各个顶点与加入最小生成树的顶点之间的最小距离
vis = [False]*n # 表示是否已经加入到了最小生成树里面
d[0]= 0 # 选择第一个点作为起始点,将其距离设为0,表示到自身的距离为0
cost = 0 # 最小生成树的总费用
# 遍历每个顶点,将其加入到最小生成树中
for _ in range(n): #也可替换成while循环
# 寻找当前轮的最小d
m = float("inf")
node = -1 # 用于记录当前轮中距离最小的点
for i in range(n):
# 如果顶点i未加入到最小生成树,并且与已加入点之间的距离小于当前最小距离,则更新最小距离
if not vis[i] and d[i] < m:
node = i
m = d[i]
vis[node] = True # 将该点标记为已加入最小生成树
cost += m # 更新最小生成树的总费用
# 更新与加入的顶点相连接的顶点的d
for i in range(n):
# 如果顶点i未加入到最小生成树,则更新其与加入顶点的距离
if not vis[i]:
# 计算顶点i与加入顶点之间的曼哈顿距离,并更新距离列表d[i]
d[i] = min(d[i],abs(points[i][0]-points[node][0])+abs(points[i][1]-points[node][1]))
return cost
总结比较:
- Kruskal算法:基于边的选择,适用于稀疏图,实现相对简单,使用并查集来检测环。
- Prim算法:基于节点的选择,适用于稠密图,实现相对简单,使用优先队列来选择最小权重的边。
在选择算法时,可以根据具体的图的特点来决定使用哪种算法。如果图比较稀疏,即边数相对节点数较少,则Kruskal算法可能更有效率;而如果图比较稠密,即边数接近节点数的平方,则Prim算法可能更合适。
标签:Prim,Kruskal,最小,生成,算法,points,节点 From: https://www.cnblogs.com/taixian/p/18095594