2024牛客寒假算法基础集训营2

C. Tokitsukaze and Min-Max XOR

题解：01 Trie

• 观察后发现对序列 \(a\) 排序并不影响结果
• 然后容易知道，对于 \(i < j, a_i \oplus a_j \leq k\) ，一共有 \(2^{i - j - 1}\) 种序列 \(b\) 满足条件，特别的，如果 \(i = j\)，只有 \(1\) 种满足条件
• 那么现在问题就转换为，我们固定 \(a_j\) 作为最大值，然后枚举 \(a_i\) \((i < j)\) 作为最小值，如果满足题目的限制条件，那么就统计对答案的贡献
• 但是这样枚举显然是 \(O(n^2)\) 的，考虑优化
• 由于是异或，我们考虑 01 Trie
• 我们再将题目转化一下：对于每个 \(a_j\)，其对答案的贡献为 \(1 + \sum_{i = 1}^{j - 1} 2^{j - i - 1}·(a_i \oplus a_j \leq k) = 1 + 2^{j - 1}\sum_{i = 1}^{j - 1} 2^{-i}·(a_i \oplus a_j \leq k)\)
• 那么我们定义 \(a_i\) 的贡献为 \(2^{-i}\)
• 然后就是在 01 Trie 上统计答案，类似求前缀中有多少个 \(a_i\) 使得 \(a_j \oplus a_i \leq k\)

D. Tokitsukaze and Slash Draw

题解：最短路

• 发现本题就是起点为 \(k\) ，终点为 \(n\) 的在模 \(n\) 意义下的最短路问题
• 对于每种操作，考虑对每个位置 \(i\) 向 \((i + a_i)\mod n\) 建边，那么边数为 \(O(nm)\)
• 然后直接跑 \(dij\) 即可

F. Tokitsukaze and Eliminate

题解

Solution 1：贪心

显然利用 \(n\) 个 vector 记录每个颜色的位置，每次挑末尾位置最小的宝石删除即可，复杂度 \(O(n)\)

Solution 2: 贪心

我们考虑如果我们需要通过删除 \(i\) 来删除其后面的所有宝石，我们必须保证 \(i\) 后面没有和 \(i\) 颜色相同的宝石，定义 \(nxt[i]\) 为在第 \(i\) 个宝石后面与第 \(i\) 个宝石颜色相同的宝石所在位置，即必须保证此时末尾宝石在 \([i, nxt[i] - 1]\)

如果我们对每个宝石都考虑这个问题，那么题目就转化了一个经典的贪心模型：给定 \(n\) 条线段，求用最少的线段数覆盖区间 \([1, n]\)

Solution 3：线段树优化 dp

定义 \(dp_i\) 为消除 \(i\) 及其后面所有宝石的最小操作次数，转移显然为 \(dp[i] = \min_{j = i + 1}^{nxt[i]} dp[j]\)

线段树优化即可

H. Tokitsukaze and Power Battle

题解

Solution 1：基于"区间查询最大子段和"思想

类似最大子段和，考虑线段树直接维护答案，合并时考虑 “减号” 所在位置：

• 减号在左儿子那一段，答案为左儿子包含右端点的最大答案 - 右儿子包含左端点的最小子段和
• 减号在中间，答案为左儿子包含右端点的最大子段和 - 右儿子包含左端点的最小子段和
• 减号在右儿子那一段，答案为左儿子包含右端点的最大子段和 + 右儿子包含左端点的最大答案

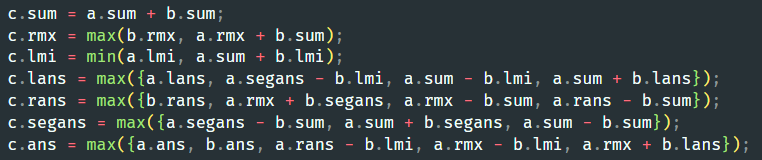
线段树维护信息如下：

• \(sum\)：区间和
• \(lmi\)：包含左端点的最小子段和
• \(rmx\)：包含右端点的最大子段和
• \(lans\)：包含左端点的最大答案
• \(rans\)：包含右端点的最大答案
• \(segans\)：包含区间左右端点的整一段的答案
• \(ans\)：区间答案

信息之间的合并：

Solution 2：线段树维护式子