标签：__ tensor self torch 程序员 FastAI 面向我们 def

原文：www.bookstack.cn/read/th-fastai-book

译者：飞龙

协议：CC BY-NC-SA 4.0

第四部分：从零开始的深度学习

第十七章：基础神经网络

原文：www.bookstack.cn/read/th-fastai-book/f6eef03cb69f6500.md

译者：飞龙

协议：CC BY-NC-SA 4.0

本章开始了一段旅程，我们将深入研究我们在前几章中使用的模型的内部。我们将涵盖许多我们以前见过的相同内容，但这一次我们将更加密切地关注实现细节，而不那么密切地关注事物为什么是这样的实际问题。

我们将从头开始构建一切，仅使用对张量的基本索引。我们将从头开始编写一个神经网络，然后手动实现反向传播，以便我们在调用loss.backward时确切地知道 PyTorch 中发生了什么。我们还将看到如何使用自定义autograd函数扩展 PyTorch，允许我们指定自己的前向和后向计算。

从头开始构建神经网络层

让我们首先刷新一下我们对基本神经网络中如何使用矩阵乘法的理解。由于我们正在从头开始构建一切，所以最初我们将仅使用纯 Python（除了对 PyTorch 张量的索引），然后在看到如何创建后，将纯 Python 替换为 PyTorch 功能。

建模神经元

神经元接收一定数量的输入，并为每个输入设置内部权重。它对这些加权输入求和以产生输出，并添加内部偏置。在数学上，这可以写成

$o u t = \sum_{i = 1}^{n} x_{i} w_{i} + b$

如果我们将输入命名为 $left-parenthesis x 1 comma ellipsis comma x Subscript n Baseline right-parenthesis$ ，我们的权重为 $left-parenthesis w 1 comma ellipsis comma w Subscript n Baseline right-parenthesis$ ，以及我们的偏置 $b$ 。在代码中，这被翻译为以下内容：

output = sum([x*w for x,w in zip(inputs,weights)]) + bias

然后将此输出馈送到非线性函数中，称为激活函数，然后发送到另一个神经元。在深度学习中，最常见的是修正线性单元，或ReLU，正如我们所见，这是一种花哨的说法：

def relu(x): return x if x >= 0 else 0

然后通过在连续的层中堆叠许多这些神经元来构建深度学习模型。我们创建一个具有一定数量的神经元（称为隐藏大小）的第一层，并将所有输入链接到每个神经元。这样的一层通常称为全连接层或密集层（用于密集连接），或线性层。

它要求您计算每个input和具有给定weight的每个神经元的点积：

sum([x*w for x,w in zip(input,weight)])

如果您对线性代数有一点了解，您可能会记得当您进行矩阵乘法时会发生许多这些点积。更准确地说，如果我们的输入在大小为batch_size乘以n_inputs的矩阵x中，并且如果我们已将神经元的权重分组在大小为n_neurons乘以n_inputs的矩阵w中（每个神经元必须具有与其输入相同数量的权重），以及将所有偏置分组在大小为n_neurons的向量b中，则此全连接层的输出为

y = x @ w.t() + b

其中@表示矩阵乘积，w.t()是w的转置矩阵。然后输出y的大小为batch_size乘以n_neurons，在位置(i,j)上我们有这个（对于数学爱好者）：

$y_{i, j} = \sum_{k = 1}^{n} x_{i, k} w_{k, j} + b_{j}$

或者在代码中：

y[i,j] = sum([a * b for a,b in zip(x[i,:],w[j,:])]) + b[j]

转置是必要的，因为在矩阵乘积m @ n的数学定义中，系数(i,j)如下：

sum([a * b for a,b in zip(m[i,:],n[:,j])])

所以我们需要的非常基本的操作是矩阵乘法，因为这是神经网络核心中隐藏的内容。

从头开始的矩阵乘法

让我们编写一个函数，计算两个张量的矩阵乘积，然后再允许我们使用 PyTorch 版本。我们只会在 PyTorch 张量中使用索引：

import torch
from torch import tensor

我们需要三个嵌套的for循环：一个用于行索引，一个用于列索引，一个用于内部求和。ac和ar分别表示a的列数和行数（对于b也是相同的约定），我们通过检查a的列数是否与b的行数相同来确保计算矩阵乘积是可能的：

def matmul(a,b):
    ar,ac = a.shape # n_rows * n_cols
    br,bc = b.shape
    assert ac==br
    c = torch.zeros(ar, bc)
    for i in range(ar):
        for j in range(bc):
            for k in range(ac): c[i,j] += a[i,k] * b[k,j]
    return c

为了测试这一点，我们假装（使用随机矩阵）我们正在处理一个包含 5 个 MNIST 图像的小批量，将它们展平为28*28向量，然后使用线性模型将它们转换为 10 个激活值：

m1 = torch.randn(5,28*28)
m2 = torch.randn(784,10)

让我们计时我们的函数，使用 Jupyter 的“魔术”命令%time：

%time t1=matmul(m1, m2)

CPU times: user 1.15 s, sys: 4.09 ms, total: 1.15 s
Wall time: 1.15 s

看看这与 PyTorch 内置的@有什么区别？

%timeit -n 20 t2=m1@m2

14 µs ± 8.95 µs per loop (mean ± std. dev. of 7 runs, 20 loops each)

正如我们所看到的，在 Python 中三个嵌套循环是一个坏主意！Python 是一种慢速语言，这不会高效。我们在这里看到 PyTorch 比 Python 快大约 100,000 倍——而且这还是在我们开始使用 GPU 之前！

这种差异是从哪里来的？PyTorch 没有在 Python 中编写矩阵乘法，而是使用 C++来加快速度。通常，当我们在张量上进行计算时，我们需要向量化它们，以便利用 PyTorch 的速度，通常使用两种技术：逐元素算术和广播。

逐元素算术

所有基本运算符（+、-、*、/、>、<、==）都可以逐元素应用。这意味着如果我们为两个具有相同形状的张量a和b写a+b，我们将得到一个由a和b元素之和组成的张量：

a = tensor([10., 6, -4])
b = tensor([2., 8, 7])
a + b

tensor([12., 14.,  3.])

布尔运算符将返回一个布尔数组：

a < b

tensor([False,  True,  True])

如果我们想知道a的每个元素是否小于b中对应的元素，或者两个张量是否相等，我们需要将这些逐元素操作与torch.all结合起来：

(a < b).all(), (a==b).all()

(tensor(False), tensor(False))

像all、sum和mean这样的缩减操作返回只有一个元素的张量，称为秩-0 张量。如果要将其转换为普通的 Python 布尔值或数字，需要调用.item：

(a + b).mean().item()

9.666666984558105

逐元素操作适用于任何秩的张量，只要它们具有相同的形状：

m = tensor([[1., 2, 3], [4,5,6], [7,8,9]])
m*m

tensor([[ 1.,  4.,  9.],
        [16., 25., 36.],
        [49., 64., 81.]])

但是，不能对形状不同的张量执行逐元素操作（除非它们是可广播的，如下一节所讨论的）：

n = tensor([[1., 2, 3], [4,5,6]])
m*n

 RuntimeError: The size of tensor a (3) must match the size of tensor b (2) at
 dimension 0

通过逐元素算术，我们可以去掉我们的三个嵌套循环中的一个：我们可以在将a的第i行和b的第j列对应的张量相乘之前对它们进行求和，这将加快速度，因为内部循环现在将由 PyTorch 以 C 速度执行。

要访问一列或一行，我们可以简单地写a[i,：]或b[:,j]。:表示在该维度上取所有内容。我们可以限制这个并只取该维度的一个切片，通过传递一个范围，比如1:5，而不仅仅是:。在这种情况下，我们将取第 1 到第 4 列的元素（第二个数字是不包括在内的）。

一个简化是我们总是可以省略尾随冒号，因此a[i,:]可以缩写为a[i]。考虑到所有这些，我们可以编写我们矩阵乘法的新版本：

def matmul(a,b):
    ar,ac = a.shape
    br,bc = b.shape
    assert ac==br
    c = torch.zeros(ar, bc)
    for i in range(ar):
        for j in range(bc): c[i,j] = (a[i] * b[:,j]).sum()
    return c

%timeit -n 20 t3 = matmul(m1,m2)

1.7 ms ± 88.1 µs per loop (mean ± std. dev. of 7 runs, 20 loops each)

我们已经快了约 700 倍，只是通过删除那个内部的for循环！这只是开始——通过广播，我们可以删除另一个循环并获得更重要的加速。

广播

正如我们在第四章中讨论的那样，广播是由Numpy 库引入的一个术语，用于描述在算术操作期间如何处理不同秩的张量。例如，显然无法将 3×3 矩阵与 4×5 矩阵相加，但如果我们想将一个标量（可以表示为 1×1 张量）与矩阵相加呢？或者大小为 3 的向量与 3×4 矩阵？在这两种情况下，我们可以找到一种方法来理解这个操作。

广播为编码规则提供了特定的规则，用于在尝试进行逐元素操作时确定形状是否兼容，以及如何扩展较小形状的张量以匹配较大形状的张量。如果您想要能够编写快速执行的代码，掌握这些规则是至关重要的。在本节中，我们将扩展我们之前对广播的处理，以了解这些规则。

使用标量进行广播

使用标量进行广播是最简单的广播类型。当我们有一个张量a和一个标量时，我们只需想象一个与a形状相同且填充有该标量的张量，并执行操作：

a = tensor([10., 6, -4])
a > 0

tensor([ True,  True, False])

我们如何能够进行这种比较？0被广播以具有与a相同的维度。请注意，这是在不在内存中创建一个充满零的张量的情况下完成的（这将是低效的）。

如果要通过减去均值（标量）来标准化数据集（矩阵）并除以标准差（另一个标量），这是很有用的：

m = tensor([[1., 2, 3], [4,5,6], [7,8,9]])
(m - 5) / 2.73

tensor([[-1.4652, -1.0989, -0.7326],
        [-0.3663,  0.0000,  0.3663],
        [ 0.7326,  1.0989,  1.4652]])

如果矩阵的每行有不同的均值怎么办？在这种情况下，您需要将一个向量广播到一个矩阵。

将向量广播到矩阵

我们可以将一个向量广播到一个矩阵中：

c = tensor([10.,20,30])
m = tensor([[1., 2, 3], [4,5,6], [7,8,9]])
m.shape,c.shape

(torch.Size([3, 3]), torch.Size([3]))

m + c

tensor([[11., 22., 33.],
        [14., 25., 36.],
        [17., 28., 39.]])

这里，c的元素被扩展为使三行匹配，从而使操作成为可能。同样，PyTorch 实际上并没有在内存中创建三个c的副本。这是由幕后的expand_as方法完成的：

c.expand_as(m)

tensor([[10., 20., 30.],
        [10., 20., 30.],
        [10., 20., 30.]])

如果我们查看相应的张量，我们可以请求其storage属性（显示用于张量的内存实际内容）来检查是否存储了无用的数据：

t = c.expand_as(m)
t.storage()

 10.0
 20.0
 30.0
[torch.FloatStorage of size 3]

尽管张量在官方上有九个元素，但内存中只存储了三个标量。这是可能的，这要归功于给该维度一个 0 步幅的巧妙技巧。在该维度上（这意味着当 PyTorch 通过添加步幅查找下一行时，它不会移动）：

t.stride(), t.shape

((0, 1), torch.Size([3, 3]))

由于m的大小为 3×3，有两种广播的方式。在最后一个维度上进行广播的事实是一种约定，这是来自广播规则的规定，与我们对张量排序的方式无关。如果我们这样做，我们会得到相同的结果：

c + m

tensor([[11., 22., 33.],
        [14., 25., 36.],
        [17., 28., 39.]])

实际上，只有通过n，我们才能将大小为n的向量广播到大小为m的矩阵中：

c = tensor([10.,20,30])
m = tensor([[1., 2, 3], [4,5,6]])
c+m

tensor([[11., 22., 33.],
        [14., 25., 36.]])

这不起作用：

c = tensor([10.,20])
m = tensor([[1., 2, 3], [4,5,6]])
c+m

 RuntimeError: The size of tensor a (2) must match the size of tensor b (3) at
 dimension 1

如果我们想在另一个维度上进行广播，我们必须改变向量的形状，使其成为一个 3×1 矩阵。这可以通过 PyTorch 中的unsqueeze方法来实现：

c = tensor([10.,20,30])
m = tensor([[1., 2, 3], [4,5,6], [7,8,9]])
c = c.unsqueeze(1)
m.shape,c.shape

(torch.Size([3, 3]), torch.Size([3, 1]))

这次，c在列侧进行了扩展：

c+m

tensor([[11., 12., 13.],
        [24., 25., 26.],
        [37., 38., 39.]])

与以前一样，只有三个标量存储在内存中：

t = c.expand_as(m)
t.storage()

 10.0
 20.0
 30.0
[torch.FloatStorage of size 3]

扩展后的张量具有正确的形状，因为列维度的步幅为 0：

t.stride(), t.shape

((1, 0), torch.Size([3, 3]))

使用广播，如果需要添加维度，则默认情况下会在开头添加。在之前进行广播时，PyTorch 在幕后执行了c.unsqueeze(0)：

c = tensor([10.,20,30])
c.shape, c.unsqueeze(0).shape,c.unsqueeze(1).shape

(torch.Size([3]), torch.Size([1, 3]), torch.Size([3, 1]))

unsqueeze命令可以被None索引替换：

c.shape, c[None,:].shape,c[:,None].shape

(torch.Size([3]), torch.Size([1, 3]), torch.Size([3, 1]))

您可以始终省略尾随冒号，...表示所有前面的维度：

c[None].shape,c[...,None].shape

(torch.Size([1, 3]), torch.Size([3, 1]))

有了这个，我们可以在我们的矩阵乘法函数中删除另一个for循环。现在，我们不再将a[i]乘以b[:,j]，而是使用广播将a[i]乘以整个矩阵b，然后对结果求和：

def matmul(a,b):
    ar,ac = a.shape
    br,bc = b.shape
    assert ac==br
    c = torch.zeros(ar, bc)
    for i in range(ar):
#       c[i,j] = (a[i,:]          * b[:,j]).sum() # previous
        c[i]   = (a[i  ].unsqueeze(-1) * b).sum(dim=0)
    return c

%timeit -n 20 t4 = matmul(m1,m2)

357 µs ± 7.2 µs per loop (mean ± std. dev. of 7 runs, 20 loops each)

现在我们比第一次实现快了 3700 倍！在继续之前，让我们更详细地讨论一下广播规则。

广播规则

在操作两个张量时，PyTorch 会逐个元素地比较它们的形状。它从尾部维度开始，逆向工作，在遇到空维度时添加 1。当以下情况之一为真时，两个维度是兼容的：

它们是相等的。
其中之一是 1，此时该维度会被广播以使其与其他维度相同。

数组不需要具有相同数量的维度。例如，如果您有一个 256×256×3 的 RGB 值数组，并且想要按不同值缩放图像中的每种颜色，您可以将图像乘以一个具有三个值的一维数组。根据广播规则排列这些数组的尾部轴的大小表明它们是兼容的：

Image  (3d tensor): 256 x 256 x 3
Scale  (1d tensor):  (1)   (1)  3
Result (3d tensor): 256 x 256 x 3

然而，一个大小为 256×256 的 2D 张量与我们的图像不兼容：

Image  (3d tensor): 256 x 256 x   3
Scale  (1d tensor):  (1)  256 x 256
Error

在我们早期的例子中，使用了一个 3×3 矩阵和一个大小为 3 的向量，广播是在行上完成的：

Matrix (2d tensor):   3 x 3
Vector (1d tensor): (1)   3
Result (2d tensor):   3 x 3

作为练习，尝试确定何时需要添加维度（以及在何处），以便将大小为64 x 3 x 256 x 256的图像批次与三个元素的向量（一个用于均值，一个用于标准差）进行归一化。

另一种简化张量操作的有用方法是使用爱因斯坦求和约定。

爱因斯坦求和

在使用 PyTorch 操作@或torch.matmul之前，我们可以实现矩阵乘法的最后一种方法：爱因斯坦求和（einsum）。这是一种将乘积和求和以一般方式组合的紧凑表示。我们可以写出这样的方程：

ik,kj -> ij

左侧表示操作数的维度，用逗号分隔。这里我们有两个分别具有两个维度（i,k和k,j）的张量。右侧表示结果维度，所以这里我们有一个具有两个维度i,j的张量。

爱因斯坦求和符号的规则如下：

重复的索引会被隐式求和。
每个索引在任何项中最多只能出现两次。
每个项必须包含相同的非重复索引。

因此，在我们的例子中，由于k是重复的，我们对该索引求和。最终，该公式表示当我们在（i,j）中放入所有第一个张量中的系数（i,k）与第二个张量中的系数（k,j）相乘的总和时得到的矩阵……这就是矩阵乘积！

以下是我们如何在 PyTorch 中编写这段代码：

def matmul(a,b): return torch.einsum('ik,kj->ij', a, b)

爱因斯坦求和是一种非常实用的表达涉及索引和乘积和的操作的方式。请注意，您可以在左侧只有一个成员。例如，

torch.einsum('ij->ji', a)

返回矩阵a的转置。您也可以有三个或更多成员：

torch.einsum('bi,ij,bj->b', a, b, c)

这将返回一个大小为b的向量，其中第k个坐标是a[k,i] b[i,j] c[k,j]的总和。当您有更多维度时，这种表示特别方便，因为有批次。例如，如果您有两批次的矩阵并且想要计算每批次的矩阵乘积，您可以这样做：

torch.einsum('bik,bkj->bij', a, b)

让我们回到使用einsum实现的新matmul，看看它的速度：

%timeit -n 20 t5 = matmul(m1,m2)

68.7 µs ± 4.06 µs per loop (mean ± std. dev. of 7 runs, 20 loops each)

正如您所看到的，它不仅实用，而且非常快。einsum通常是在 PyTorch 中执行自定义操作的最快方式，而无需深入研究 C++和 CUDA。（但通常不如精心优化的 CUDA 代码快，正如您从“从头开始的矩阵乘法”的结果中看到的。）

现在我们知道如何从头开始实现矩阵乘法，我们准备构建我们的神经网络——具体来说，是它的前向和后向传递——只使用矩阵乘法。

前向和后向传递

正如我们在第四章中看到的，为了训练一个模型，我们需要计算给定损失对其参数的所有梯度，这被称为反向传播。在前向传播中，我们根据矩阵乘积计算给定输入上模型的输出。当我们定义我们的第一个神经网络时，我们还将深入研究适当初始化权重的问题，这对于使训练正确开始至关重要。

定义和初始化一个层

首先我们将以两层神经网络为例。正如我们所看到的，一层可以表示为y = x @ w + b，其中x是我们的输入，y是我们的输出，w是该层的权重（如果我们不像之前那样转置，则大小为输入数量乘以神经元数量），b是偏置向量：

def lin(x, w, b): return x @ w + b

我们可以将第二层叠加在第一层上，但由于数学上两个线性操作的组合是另一个线性操作，只有在中间放入一些非线性的东西才有意义，称为激活函数。正如本章开头提到的，在深度学习应用中，最常用的激活函数是 ReLU，它返回x和0的最大值。

在本章中，我们实际上不会训练我们的模型，因此我们将为我们的输入和目标使用随机张量。假设我们的输入是大小为 100 的 200 个向量，我们将它们分组成一个批次，我们的目标是 200 个随机浮点数：

x = torch.randn(200, 100)
y = torch.randn(200)

对于我们的两层模型，我们将需要两个权重矩阵和两个偏置向量。假设我们的隐藏大小为 50，输出大小为 1（对于我们的输入之一，相应的输出在这个玩具示例中是一个浮点数）。我们随机初始化权重，偏置为零：

w1 = torch.randn(100,50)
b1 = torch.zeros(50)
w2 = torch.randn(50,1)
b2 = torch.zeros(1)

然后我们的第一层的结果就是这样的：

l1 = lin(x, w1, b1)
l1.shape

torch.Size([200, 50])

请注意，这个公式适用于我们的输入批次，并返回一个隐藏状态批次：l1是一个大小为 200（我们的批次大小）乘以 50（我们的隐藏大小）的矩阵。

然而，我们的模型初始化方式存在问题。要理解这一点，我们需要查看l1的均值和标准差（std）：

l1.mean(), l1.std()

(tensor(0.0019), tensor(10.1058))

均值接近零，这是可以理解的，因为我们的输入和权重矩阵的均值都接近零。但标准差，表示我们的激活离均值有多远，从 1 变为 10。这是一个真正的大问题，因为这只是一个层。现代神经网络可以有数百层，因此如果每一层将我们的激活的规模乘以 10，到了最后一层，我们将无法用计算机表示数字。

实际上，如果我们在x和大小为 100×100 的随机矩阵之间进行 50 次乘法运算，我们将得到这个结果：

x = torch.randn(200, 100)
for i in range(50): x = x @ torch.randn(100,100)
x[0:5,0:5]

tensor([[nan, nan, nan, nan, nan],
        [nan, nan, nan, nan, nan],
        [nan, nan, nan, nan, nan],
        [nan, nan, nan, nan, nan],
        [nan, nan, nan, nan, nan]])

结果是到处都是nan。也许我们的矩阵的规模太大了，我们需要更小的权重？但如果我们使用太小的权重，我们将遇到相反的问题-我们的激活的规模将从 1 变为 0.1，在 100 层之后，我们将到处都是零：

x = torch.randn(200, 100)
for i in range(50): x = x @ (torch.randn(100,100) * 0.01)
x[0:5,0:5]

tensor([[0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.]])

因此，我们必须精确地缩放我们的权重矩阵，以使我们的激活的标准差保持在 1。我们可以通过数学计算出要使用的确切值，正如 Xavier Glorot 和 Yoshua Bengio 在“理解训练深度前馈神经网络的困难”中所示。给定层的正确比例是 $1 slash StartRoot n Subscript i n Baseline EndRoot$ ，其中 $n_{i n}$ 代表输入的数量。

在我们的情况下，如果有 100 个输入，我们应该将我们的权重矩阵缩放为 0.1：

x = torch.randn(200, 100)
for i in range(50): x = x @ (torch.randn(100,100) * 0.1)
x[0:5,0:5]

tensor([[ 0.7554,  0.6167, -0.1757, -1.5662,  0.5644],
        [-0.1987,  0.6292,  0.3283, -1.1538,  0.5416],
        [ 0.6106,  0.2556, -0.0618, -0.9463,  0.4445],
        [ 0.4484,  0.7144,  0.1164, -0.8626,  0.4413],
        [ 0.3463,  0.5930,  0.3375, -0.9486,  0.5643]])

终于，一些既不是零也不是nan的数字！请注意，即使经过了那 50 个虚假层，我们的激活的规模仍然是稳定的：

x.std()

tensor(0.7042)

如果你稍微调整一下 scale 的值，你会注意到即使从 0.1 稍微偏离，你会得到非常小或非常大的数字，因此正确初始化权重非常重要。

让我们回到我们的神经网络。由于我们稍微改变了我们的输入，我们需要重新定义它们：

x = torch.randn(200, 100)
y = torch.randn(200)

对于我们的权重，我们将使用正确的 scale，这被称为Xavier 初始化（或Glorot 初始化）：

from math import sqrt
w1 = torch.randn(100,50) / sqrt(100)
b1 = torch.zeros(50)
w2 = torch.randn(50,1) / sqrt(50)
b2 = torch.zeros(1)

现在如果我们计算第一层的结果，我们可以检查均值和标准差是否受控制：

l1 = lin(x, w1, b1)
l1.mean(),l1.std()

(tensor(-0.0050), tensor(1.0000))

非常好。现在我们需要经过一个 ReLU，所以让我们定义一个。ReLU 去除负数并用零替换它们，这另一种说法是它将我们的张量夹在零处：

def relu(x): return x.clamp_min(0.)

我们通过这个激活：

l2 = relu(l1)
l2.mean(),l2.std()

(tensor(0.3961), tensor(0.5783))

现在我们回到原点：我们的激活均值变为 0.4（这是可以理解的，因为我们去除了负数），标准差下降到 0.58。所以像以前一样，经过几层后我们可能最终会得到零：

x = torch.randn(200, 100)
for i in range(50): x = relu(x @ (torch.randn(100,100) * 0.1))
x[0:5,0:5]

tensor([[0.0000e+00, 1.9689e-08, 4.2820e-08, 0.0000e+00, 0.0000e+00],
        [0.0000e+00, 1.6701e-08, 4.3501e-08, 0.0000e+00, 0.0000e+00],
        [0.0000e+00, 1.0976e-08, 3.0411e-08, 0.0000e+00, 0.0000e+00],
        [0.0000e+00, 1.8457e-08, 4.9469e-08, 0.0000e+00, 0.0000e+00],
        [0.0000e+00, 1.9949e-08, 4.1643e-08, 0.0000e+00, 0.0000e+00]])

这意味着我们的初始化不正确。为什么？在 Glorot 和 Bengio 撰写他们的文章时，神经网络中最流行的激活函数是双曲正切（tanh，他们使用的那个），而该初始化并没有考虑到我们的 ReLU。幸运的是，有人已经为我们计算出了正确的 scale 供我们使用。在“深入研究整流器：超越人类水平的性能”（我们之前见过的文章，介绍了 ResNet），Kaiming He 等人表明我们应该使用以下 scale 代替： $StartRoot 2 slash n Subscript i n Baseline EndRoot$ ，其中 $n_{i n}$ 是我们模型的输入数量。让我们看看这给我们带来了什么：

x = torch.randn(200, 100)
for i in range(50): x = relu(x @ (torch.randn(100,100) * sqrt(2/100)))
x[0:5,0:5]

tensor([[0.2871, 0.0000, 0.0000, 0.0000, 0.0026],
        [0.4546, 0.0000, 0.0000, 0.0000, 0.0015],
        [0.6178, 0.0000, 0.0000, 0.0180, 0.0079],
        [0.3333, 0.0000, 0.0000, 0.0545, 0.0000],
        [0.1940, 0.0000, 0.0000, 0.0000, 0.0096]])

好了：这次我们的数字不全为零。所以让我们回到我们神经网络的定义，并使用这个初始化（被称为Kaiming 初始化或He 初始化）：

x = torch.randn(200, 100)
y = torch.randn(200)

w1 = torch.randn(100,50) * sqrt(2 / 100)
b1 = torch.zeros(50)
w2 = torch.randn(50,1) * sqrt(2 / 50)
b2 = torch.zeros(1)

让我们看看通过第一个线性层和 ReLU 后激活的规模：

l1 = lin(x, w1, b1)
l2 = relu(l1)
l2.mean(), l2.std()

(tensor(0.5661), tensor(0.8339))

好多了！现在我们的权重已经正确初始化，我们可以定义我们的整个模型：

def model(x):
    l1 = lin(x, w1, b1)
    l2 = relu(l1)
    l3 = lin(l2, w2, b2)
    return l3

这是前向传播。现在剩下的就是将我们的输出与我们拥有的标签（在这个例子中是随机数）进行比较，使用损失函数。在这种情况下，我们将使用均方误差。（这是一个玩具问题，这是下一步计算梯度所使用的最简单的损失函数。）

唯一的微妙之处在于我们的输出和目标形状并不完全相同——经过模型后，我们得到这样的输出：

out = model(x)
out.shape

torch.Size([200, 1])

为了去掉这个多余的 1 维，我们使用squeeze函数：

def mse(output, targ): return (output.squeeze(-1) - targ).pow(2).mean()

现在我们准备计算我们的损失：

loss = mse(out, y)

前向传播到此结束，现在让我们看一下梯度。

梯度和反向传播

我们已经看到 PyTorch 通过一个神奇的调用loss.backward计算出我们需要的所有梯度，但让我们探究一下背后发生了什么。

现在我们需要计算损失相对于模型中所有权重的梯度，即w1、b1、w2和b2中的所有浮点数。为此，我们需要一点数学，具体来说是链式法则。这是指导我们如何计算复合函数导数的微积分规则：

$left-parenthesis g ring f right-parenthesis prime left-parenthesis x right-parenthesis equals g prime left-parenthesis f left-parenthesis x right-parenthesis right-parenthesis f prime left-parenthesis x right-parenthesis$

Jeremy 说

我发现这种符号很难理解，所以我喜欢这样想：如果 y = g(u) 和 u=f(x)，那么 dy/dx = dy/du * du/dx。这两种符号意思相同，所以使用任何一种都可以。

我们的损失是不同函数的大组合：均方误差（实际上是均值和平方的组合），第二个线性层，一个 ReLU，和第一个线性层。例如，如果我们想要损失相对于 b2 的梯度，而我们的损失由以下定义：

loss = mse(out,y) = mse(lin(l2, w2, b2), y)

链式法则告诉我们我们有这个：

$\frac{d l o s s}{d b_{2}} = \frac{d l o s s}{d o u t} \times \frac{d o u t}{d b_{2}} = \frac{d}{d o u t} m s e (o u t, y) \times \frac{d}{d b_{2}} l i n (l_{2}, w_{2}, b_{2})$

要计算损失相对于 $b 2$ 的梯度，我们首先需要损失相对于我们的输出 $o u t$ 的梯度。如果我们想要损失相对于 $w 2$ 的梯度也是一样的。然后，要得到损失相对于 $b 1$ 或 $w 1$ 的梯度，我们将需要损失相对于 $l 1$ 的梯度，这又需要损失相对于 $l 2$ 的梯度，这将需要损失相对于 $o u t$ 的梯度。

因此，为了计算更新所需的所有梯度，我们需要从模型的输出开始，逐层向后工作，一层接一层地——这就是为什么这一步被称为反向传播。我们可以通过让我们实现的每个函数（relu、mse、lin）提供其反向步骤来自动化它：也就是说，如何从损失相对于输出的梯度推导出损失相对于输入的梯度。

在这里，我们将这些梯度填充到每个张量的属性中，有点像 PyTorch 在.grad中所做的那样。

首先是我们模型输出（损失函数的输入）相对于损失的梯度。我们撤消了mse中的squeeze，然后我们使用给出 $x^{2}$ 的导数的公式： $2 x$ 。均值的导数只是 1/n，其中n是我们输入中的元素数：

def mse_grad(inp, targ):
    # grad of loss with respect to output of previous layer
    inp.g = 2. * (inp.squeeze() - targ).unsqueeze(-1) / inp.shape[0]

对于 ReLU 和我们的线性层的梯度，我们使用相对于输出的损失的梯度（在out.g中）并应用链式法则来计算相对于输出的损失的梯度（在inp.g中）。链式法则告诉我们inp.g = relu'(inp) * out.g。relu的导数要么是 0（当输入为负数时），要么是 1（当输入为正数时），因此这给出了以下结果：

def relu_grad(inp, out):
    # grad of relu with respect to input activations
    inp.g = (inp>0).float() * out.g

计算损失相对于线性层中的输入、权重和偏差的梯度的方案是相同的：

def lin_grad(inp, out, w, b):
    # grad of matmul with respect to input
    inp.g = out.g @ w.t()
    w.g = inp.t() @ out.g
    b.g = out.g.sum(0)

我们不会深入讨论定义它们的数学公式，因为对我们的目的来说它们不重要，但如果你对这个主题感兴趣，可以查看可汗学院出色的微积分课程。

一旦我们定义了这些函数，我们就可以使用它们来编写后向传递。由于每个梯度都会自动填充到正确的张量中，我们不需要将这些_grad函数的结果存储在任何地方——我们只需要按照前向传递的相反顺序执行它们，以确保在每个函数中out.g存在：

def forward_and_backward(inp, targ):
    # forward pass:
    l1 = inp @ w1 + b1
    l2 = relu(l1)
    out = l2 @ w2 + b2
    # we don't actually need the loss in backward!
    loss = mse(out, targ)

    # backward pass:
    mse_grad(out, targ)
    lin_grad(l2, out, w2, b2)
    relu_grad(l1, l2)
    lin_grad(inp, l1, w1, b1)

现在我们可以在w1.g、b1.g、w2.g和b2.g中访问我们模型参数的梯度。我们已经成功定义了我们的模型——现在让我们让它更像一个 PyTorch 模块。

重构模型

我们使用的三个函数有两个相关的函数：一个前向传递和一个后向传递。我们可以创建一个类将它们包装在一起，而不是分开编写它们。该类还可以存储后向传递的输入和输出。这样，我们只需要调用backward：

class Relu():
    def __call__(self, inp):
        self.inp = inp
        self.out = inp.clamp_min(0.)
        return self.out

    def backward(self): self.inp.g = (self.inp>0).float() * self.out.g

__call__是 Python 中的一个魔术名称，它将使我们的类可调用。当我们键入y = Relu()(x)时，将执行这个操作。我们也可以对我们的线性层和 MSE 损失做同样的操作：

class Lin():
    def __init__(self, w, b): self.w,self.b = w,b

    def __call__(self, inp):
        self.inp = inp
        self.out = [email protected] + self.b
        return self.out

    def backward(self):
        self.inp.g = self.out.g @ self.w.t()
        self.w.g = self.inp.t() @ self.out.g
        self.b.g = self.out.g.sum(0)

class Mse():
    def __call__(self, inp, targ):
        self.inp = inp
        self.targ = targ
        self.out = (inp.squeeze() - targ).pow(2).mean()
        return self.out

    def backward(self):
        x = (self.inp.squeeze()-self.targ).unsqueeze(-1)
        self.inp.g = 2.*x/self.targ.shape[0]

然后我们可以把一切都放在一个模型中，我们用我们的张量w1、b1、w2和b2来初始化：

class Model():
    def __init__(self, w1, b1, w2, b2):
        self.layers = [Lin(w1,b1), Relu(), Lin(w2,b2)]
        self.loss = Mse()

    def __call__(self, x, targ):
        for l in self.layers: x = l(x)
        return self.loss(x, targ)

    def backward(self):
        self.loss.backward()
        for l in reversed(self.layers): l.backward()

这种重构和将事物注册为模型的层的好处是，前向和后向传递现在非常容易编写。如果我们想要实例化我们的模型，我们只需要写这个：

model = Model(w1, b1, w2, b2)

然后前向传递可以这样执行：

loss = model(x, y)

然后使用这个进行后向传递：

model.backward()

转向 PyTorch

我们编写的Lin、Mse和Relu类有很多共同之处，所以我们可以让它们都继承自同一个基类：

class LayerFunction():
    def __call__(self, *args):
        self.args = args
        self.out = self.forward(*args)
        return self.out

    def forward(self):  raise Exception('not implemented')
    def bwd(self):      raise Exception('not implemented')
    def backward(self): self.bwd(self.out, *self.args)

然后我们只需要在每个子类中实现forward和bwd：

class Relu(LayerFunction):
    def forward(self, inp): return inp.clamp_min(0.)
    def bwd(self, out, inp): inp.g = (inp>0).float() * out.g

class Lin(LayerFunction):
    def __init__(self, w, b): self.w,self.b = w,b

    def forward(self, inp): return [email protected] + self.b

    def bwd(self, out, inp):
        inp.g = out.g @ self.w.t()
        self.w.g = self.inp.t() @ self.out.g
        self.b.g = out.g.sum(0)

class Mse(LayerFunction):
    def forward (self, inp, targ): return (inp.squeeze() - targ).pow(2).mean()
    def bwd(self, out, inp, targ):
        inp.g = 2*(inp.squeeze()-targ).unsqueeze(-1) / targ.shape[0]

我们模型的其余部分可以与以前相同。这越来越接近 PyTorch 的做法。我们需要区分的每个基本函数都被写成一个torch.autograd.Function对象，它有一个forward和一个backward方法。PyTorch 将跟踪我们进行的任何计算，以便能够正确运行反向传播，除非我们将张量的requires_grad属性设置为False。

编写其中一个（几乎）和编写我们原始类一样容易。不同之处在于我们选择保存什么并将其放入上下文变量中（以确保我们不保存不需要的任何内容），并在backward传递中返回梯度。很少需要编写自己的Function，但如果您需要某些奇特的东西或想要干扰常规函数的梯度，这里是如何编写的：

from torch.autograd import Function

class MyRelu(Function):
    @staticmethod
    def forward(ctx, i):
        result = i.clamp_min(0.)
        ctx.save_for_backward(i)
        return result

    @staticmethod
    def backward(ctx, grad_output):
        i, = ctx.saved_tensors
        return grad_output * (i>0).float()

用于构建利用这些Function的更复杂模型的结构是torch.nn.Module。这是所有模型的基本结构，到目前为止您看到的所有神经网络都是从该类中继承的。它主要有助于注册所有可训练的参数，正如我们已经看到的可以在训练循环中使用的那样。

要实现一个nn.Module，你只需要做以下几步：

确保在初始化时首先调用超类__init__。
将模型的任何参数定义为具有nn.Parameter属性。
定义一个forward函数，返回模型的输出。

这里是一个从头开始的线性层的例子：

import torch.nn as nn

class LinearLayer(nn.Module):
    def __init__(self, n_in, n_out):
        super().__init__()
        self.weight = nn.Parameter(torch.randn(n_out, n_in) * sqrt(2/n_in))
        self.bias = nn.Parameter(torch.zeros(n_out))

    def forward(self, x): return x @ self.weight.t() + self.bias

正如您所看到的，这个类会自动跟踪已定义的参数：

lin = LinearLayer(10,2)
p1,p2 = lin.parameters()
p1.shape,p2.shape

(torch.Size([2, 10]), torch.Size([2]))

正是由于nn.Module的这个特性，我们可以只说opt.step，并让优化器循环遍历参数并更新每个参数。

请注意，在 PyTorch 中，权重存储为一个n_out x n_in矩阵，这就是为什么在前向传递中我们有转置的原因。

通过使用 PyTorch 中的线性层（也使用 Kaiming 初始化），我们在本章中一直在构建的模型可以这样编写：

class Model(nn.Module):
    def __init__(self, n_in, nh, n_out):
        super().__init__()
        self.layers = nn.Sequential(
            nn.Linear(n_in,nh), nn.ReLU(), nn.Linear(nh,n_out))
        self.loss = mse

    def forward(self, x, targ): return self.loss(self.layers(x).squeeze(), targ)

fastai 提供了自己的Module变体，与nn.Module相同，但不需要您调用super().__init__()（它会自动为您执行）：

class Model(Module):
    def __init__(self, n_in, nh, n_out):
        self.layers = nn.Sequential(
            nn.Linear(n_in,nh), nn.ReLU(), nn.Linear(nh,n_out))
        self.loss = mse

    def forward(self, x, targ): return self.loss(self.layers(x).squeeze(), targ)

在第十九章中，我们将从这样一个模型开始，看看如何从头开始构建一个训练循环，并将其重构为我们在之前章节中使用的内容。

结论

在本章中，我们探讨了深度学习的基础，从矩阵乘法开始，然后实现了神经网络的前向和反向传递。然后我们重构了我们的代码，展示了 PyTorch 在底层的工作原理。

以下是一些需要记住的事项：

神经网络基本上是一堆矩阵乘法，中间夹杂着非线性。
Python 很慢，所以为了编写快速代码，我们必须对其进行向量化，并利用诸如逐元素算术和广播等技术。
如果从末尾开始向后匹配的维度相同（如果它们相同，或者其中一个是 1），则两个张量是可广播的。为了使张量可广播，我们可能需要使用unsqueeze或None索引添加大小为 1 的维度。
正确初始化神经网络对于开始训练至关重要。当我们有 ReLU 非线性时，应使用 Kaiming 初始化。
反向传递是应用链式法则多次计算，从我们模型的输出开始，逐层向后计算梯度。
在子类化nn.Module时（如果不使用 fastai 的Module），我们必须在我们的__init__方法中调用超类__init__方法，并且我们必须定义一个接受输入并返回所需结果的forward函数。

问卷

编写 Python 代码来实现一个单个神经元。
编写实现 ReLU 的 Python 代码。
用矩阵乘法的术语编写一个密集层的 Python 代码。
用纯 Python 编写一个密集层的 Python 代码（即使用列表推导和内置到 Python 中的功能）。
一个层的“隐藏大小”是什么？
在 PyTorch 中，t方法是做什么的？
为什么在纯 Python 中编写矩阵乘法非常慢？
在matmul中，为什么ac==br？
在 Jupyter Notebook 中，如何测量执行单个单元格所需的时间？
什么是逐元素算术？
编写 PyTorch 代码来测试 a 的每个元素是否大于 b 的对应元素。
什么是秩为 0 的张量？如何将其转换为普通的 Python 数据类型？
这返回什么，为什么？
```
tensor([1,2]) + tensor([1])
```
这返回什么，为什么？
```
tensor([1,2]) + tensor([1,2,3])
```
逐元素算术如何帮助我们加速 matmul？
广播规则是什么？
expand_as 是什么？展示一个如何使用它来匹配广播结果的示例。
unsqueeze 如何帮助我们解决某些广播问题？
我们如何使用索引来执行与 unsqueeze 相同的操作？
我们如何显示张量使用的内存的实际内容？
将大小为 3 的向量添加到大小为 3×3 的矩阵时，向量的元素是添加到矩阵的每一行还是每一列？（确保通过在笔记本中运行此代码来检查您的答案。）
广播和 expand_as 会导致内存使用增加吗？为什么或为什么不？
使用爱因斯坦求和实现 matmul。
在 einsum 的左侧重复索引字母代表什么？
爱因斯坦求和符号的三条规则是什么？为什么？
神经网络的前向传播和反向传播是什么？
为什么我们需要在前向传播中存储一些计算出的中间层的激活？
具有标准差远离 1 的激活的缺点是什么？
权重初始化如何帮助避免这个问题？
初始化权重的公式是什么，以便在普通线性层和 ReLU 后跟线性层中获得标准差为 1？
为什么有时我们必须在损失函数中使用 squeeze 方法？
squeeze 方法的参数是做什么的？为什么可能很重要包含这个参数，尽管 PyTorch 不需要它？
链式法则是什么？展示本章中提出的两种形式中的任意一种方程。
展示如何使用链式法则计算 mse(lin(l2, w2, b2), y) 的梯度。
ReLU 的梯度是什么？用数学或代码展示它。（您不应该需要记住这个—尝试使用您对函数形状的知识来弄清楚它。）
在反向传播中，我们需要以什么顺序调用 *_grad 函数？为什么？
__call__ 是什么？
编写 torch.autograd.Function 时我们必须实现哪些方法？
从头开始编写 nn.Linear 并测试其是否有效。
nn.Module 和 fastai 的 Module 之间有什么区别？

进一步研究

将 ReLU 实现为 torch.autograd.Function 并用它训练模型。
如果您对数学感兴趣，请确定数学符号中线性层的梯度。将其映射到本章中的实现。
了解 PyTorch 中的 unfold 方法，并结合矩阵乘法实现自己的二维卷积函数。然后训练一个使用它的 CNN。
使用 NumPy 而不是 PyTorch 在本章中实现所有内容。

第十八章：使用 CAM 解释 CNN

原文：www.bookstack.cn/read/th-fastai-book/20b17a5a56ea9b6f.md

译者：飞龙

协议：CC BY-NC-SA 4.0

现在我们知道如何从头开始构建几乎任何东西，让我们利用这些知识来创建全新（并非常有用！）的功能：类激活图。它让我们对 CNN 为何做出预测有一些见解。

在这个过程中，我们将学习到 PyTorch 中一个我们之前没有见过的方便功能，hook，并且我们将应用本书中介绍的许多概念。如果你想真正测试你对本书材料的理解，完成本章后，尝试将其放在一边，从头开始重新创建这里的想法（不要偷看！）。

CAM 和 Hooks

类激活图（CAM）是由周博磊等人在“学习用于区分定位的深度特征”中引入的。它使用最后一个卷积层的输出（就在平均池化层之前）以及预测结果，为我们提供一个热图可视化，解释模型为何做出决定。这是一个有用的解释工具。

更准确地说，在我们最终卷积层的每个位置，我们有与最后一个线性层中一样多的滤波器。因此，我们可以计算这些激活与最终权重的点积，以便为我们特征图上的每个位置得到用于做出决定的特征的分数。

在训练模型时，我们需要一种方法来访问模型内部的激活。在 PyTorch 中，可以通过 hook 来实现。Hook 是 PyTorch 的等价于 fastai 的回调。然而，与允许您像 fastai 的 Learner 回调一样将代码注入训练循环不同，hook 允许您将代码注入前向和反向计算本身。我们可以将 hook 附加到模型的任何层，并且在计算输出（前向 hook）或反向传播（后向 hook）时执行。前向 hook 是一个接受三个参数的函数——一个模块，它的输入和输出——它可以执行任何您想要的行为。（fastai 还提供了一个方便的 HookCallback，我们这里不涉及，但看看 fastai 文档；它使使用 hook 更容易一些。）

为了说明，我们将使用我们在第一章中训练的相同的猫狗模型：

path = untar_data(URLs.PETS)/'images'
def is_cat(x): return x[0].isupper()
dls = ImageDataLoaders.from_name_func(
    path, get_image_files(path), valid_pct=0.2, seed=21,
    label_func=is_cat, item_tfms=Resize(224))
learn = cnn_learner(dls, resnet34, metrics=error_rate)
learn.fine_tune(1)

轮次	训练损失	验证损失	错误率	时间
0	0.141987	0.018823	0.007442	00:16
轮次	训练损失	验证损失	错误率	时间
---	---	---	---	---
0	0.050934	0.015366	0.006766	00:21

首先，我们将获取一张猫的图片和一批数据：

img = PILImage.create('images/chapter1_cat_example.jpg')
x, = first(dls.test_dl([img]))

对于 CAM，我们想要存储最后一个卷积层的激活。我们将我们的 hook 函数放在一个类中，这样它就有一个我们稍后可以访问的状态，并且只存储输出的副本：

class Hook():
    def hook_func(self, m, i, o): self.stored = o.detach().clone()

然后我们可以实例化一个 Hook 并将其附加到我们想要的层，即 CNN 主体的最后一层：

hook_output = Hook()
hook = learn.model[0].register_forward_hook(hook_output.hook_func)

现在我们可以获取一个批次并将其通过我们的模型：

with torch.no_grad(): output = learn.model.eval()(x)

我们可以访问我们存储的激活：

act = hook_output.stored[0]

让我们再次双重检查我们的预测：

F.softmax(output, dim=-1)

tensor([[7.3566e-07, 1.0000e+00]], device='cuda:0')

我们知道 0（对于 False）是“狗”，因为在 fastai 中类别会自动排序，但我们仍然可以通过查看 dls.vocab 来进行双重检查：

dls.vocab

(#2) [False,True]

所以，我们的模型非常确信这是一张猫的图片。

为了对我们的权重矩阵（2 乘以激活数量）与激活（批次大小乘以激活乘以行乘以列）进行点积，我们使用自定义的 einsum：

x.shape

torch.Size([1, 3, 224, 224])

cam_map = torch.einsum('ck,kij->cij', learn.model[1][-1].weight, act)
cam_map.shape

torch.Size([2, 7, 7])

对于我们批次中的每个图像，对于每个类别，我们得到一个 7×7 的特征图，告诉我们激活较高和较低的位置。这将让我们看到哪些图片区域影响了模型的决策。

例如，我们可以找出哪些区域使模型决定这个动物是一只猫（请注意，由于DataLoader对输入x进行了归一化，我们需要decode，并且由于在撰写本书时，PyTorch 在索引时不保留类型，我们需要转换为TensorImage——这可能在您阅读本文时已经修复）：

x_dec = TensorImage(dls.train.decode((x,))[0][0])
_,ax = plt.subplots()
x_dec.show(ctx=ax)
ax.imshow(cam_map[1].detach().cpu(), alpha=0.6, extent=(0,224,224,0),
              interpolation='bilinear', cmap='magma');

在这种情况下，明亮黄色的区域对应于高激活，紫色区域对应于低激活。在这种情况下，我们可以看到头部和前爪是使模型决定这是一张猫的图片的两个主要区域。

完成钩子后，应该将其删除，否则可能会泄漏一些内存：

hook.remove()

这就是为什么将Hook类作为上下文管理器通常是一个好主意，当您进入时注册钩子，当您退出时删除它。上下文管理器是一个 Python 构造，在with子句中创建对象时调用__enter__，在with子句结束时调用__exit__。例如，这就是 Python 处理with open(...) as f:构造的方式，您经常会看到用于打开文件而不需要在最后显式调用close(f)。

如果我们将Hook定义如下

class Hook():
    def __init__(self, m):
        self.hook = m.register_forward_hook(self.hook_func)
    def hook_func(self, m, i, o): self.stored = o.detach().clone()
    def __enter__(self, *args): return self
    def __exit__(self, *args): self.hook.remove()

我们可以安全地这样使用它：

with Hook(learn.model[0]) as hook:
    with torch.no_grad(): output = learn.model.eval()(x.cuda())
    act = hook.stored

fastai 为您提供了这个Hook类，以及一些其他方便的类，使使用钩子更容易。

这种方法很有用，但仅适用于最后一层。梯度 CAM是一个解决这个问题的变体。

梯度 CAM

我们刚刚看到的方法让我们只能计算最后激活的热图，因为一旦我们有了我们的特征，我们必须将它们乘以最后的权重矩阵。这对网络中的内部层不起作用。2016 年的一篇论文“Grad-CAM: Why Did You Say That?”由 Ramprasaath R. Selvaraju 等人介绍了一种变体，使用所需类的最终激活的梯度。如果您还记得一点关于反向传播的知识，最后一层输出的梯度与该层输入的梯度相对应，因为它是一个线性层。

对于更深的层，我们仍然希望梯度，但它们不再等于权重。我们必须计算它们。PyTorch 在反向传播期间为我们计算每一层的梯度，但它们不会被存储（除了requires_grad为True的张量）。然而，我们可以在反向传播上注册一个钩子，PyTorch 将把梯度作为参数传递给它，因此我们可以在那里存储它们。为此，我们将使用一个HookBwd类，它的工作方式类似于Hook，但是拦截并存储梯度而不是激活：

class HookBwd():
    def __init__(self, m):
        self.hook = m.register_backward_hook(self.hook_func)
    def hook_func(self, m, gi, go): self.stored = go[0].detach().clone()
    def __enter__(self, *args): return self
    def __exit__(self, *args): self.hook.remove()

然后对于类索引1（对于True，即“猫”），我们拦截最后一个卷积层的特征，如前所述，计算我们类的输出激活的梯度。我们不能简单地调用output.backward，因为梯度只对标量有意义（通常是我们的损失），而output是一个秩为 2 的张量。但是，如果我们选择单个图像（我们将使用0）和单个类（我们将使用1），我们可以计算我们喜欢的任何权重或激活的梯度，与该单个值相关，使用output[0,cls].backward。我们的钩子拦截了我们将用作权重的梯度：

cls = 1
with HookBwd(learn.model[0]) as hookg:
    with Hook(learn.model[0]) as hook:
        output = learn.model.eval()(x.cuda())
        act = hook.stored
    output[0,cls].backward()
    grad = hookg.stored

Grad-CAM 的权重由特征图上的梯度平均值给出。然后就像以前一样：

w = grad[0].mean(dim=[1,2], keepdim=True)
cam_map = (w * act[0]).sum(0)

_,ax = plt.subplots()
x_dec.show(ctx=ax)
ax.imshow(cam_map.detach().cpu(), alpha=0.6, extent=(0,224,224,0),
              interpolation='bilinear', cmap='magma');

Grad-CAM 的新颖之处在于我们可以在任何层上使用它。例如，在这里我们将其用于倒数第二个 ResNet 组的输出：

with HookBwd(learn.model[0][-2]) as hookg:
    with Hook(learn.model[0][-2]) as hook:
        output = learn.model.eval()(x.cuda())
        act = hook.stored
    output[0,cls].backward()
    grad = hookg.stored

w = grad[0].mean(dim=[1,2], keepdim=True)
cam_map = (w * act[0]).sum(0)

现在我们可以查看此层的激活图：

_,ax = plt.subplots()
x_dec.show(ctx=ax)
ax.imshow(cam_map.detach().cpu(), alpha=0.6, extent=(0,224,224,0),
              interpolation='bilinear', cmap='magma');

结论

模型解释是一个活跃研究领域，我们只是在这一简短章节中探讨了可能性的一部分。类激活图让我们了解模型为什么预测了某个结果，它展示了图像中对于给定预测最负责的区域。这可以帮助我们分析假阳性，并找出在我们的训练中缺少了哪种数据以避免它们。

问卷调查

PyTorch 中的 hook 是什么？
CAM 使用哪个层的输出？
为什么 CAM 需要一个 hook？
查看ActivationStats类的源代码，看看它如何使用 hooks。
编写一个 hook，用于存储模型中给定层的激活（如果可能的话，不要偷看）。
为什么我们在获取激活之前要调用eval？为什么我们要使用no_grad？
使用torch.einsum来计算模型主体最后激活的每个位置的“狗”或“猫”得分。
如何检查类别的顺序（即索引→类别的对应关系）？
为什么我们在显示输入图像时使用decode？
什么是上下文管理器？需要定义哪些特殊方法来创建一个？
为什么我们不能对网络的内部层使用普通的 CAM？
为了执行 Grad-CAM，为什么我们需要在反向传播中注册一个 hook？
当output是每个图像每个类别的输出激活的秩为 2 的张量时，为什么我们不能调用output.backward？

进一步研究

尝试移除keepdim，看看会发生什么。查阅 PyTorch 文档中的这个参数。为什么我们在这个笔记本中需要它？
创建一个类似这个的笔记本，但用于 NLP，并用它来找出电影评论中哪些词对于评估特定电影评论的情感最重要。

第十九章：从头开始创建一个 fastai 学习器

原文：www.bookstack.cn/read/th-fastai-book/5443c76c2b161687.md

译者：飞龙

协议：CC BY-NC-SA 4.0

这最后一章（除了结论和在线章节）将会有所不同。它包含的代码比以前的章节要多得多，而叙述要少得多。我们将介绍新的 Python 关键字和库，而不进行讨论。这一章的目的是为您开展一项重要的研究项目。您将看到，我们将从头开始实现 fastai 和 PyTorch API 的许多关键部分，仅建立在我们在第十七章中开发的组件上！这里的关键目标是最终拥有自己的Learner类和一些回调函数，足以训练一个模型在 Imagenette 上，包括我们学习的每个关键技术的示例。在构建Learner的过程中，我们将创建我们自己的Module、Parameter和并行DataLoader的版本，这样您就会对 PyTorch 类的功能有一个很好的了解。

本章末尾的问卷调查对于本章非常重要。这是我们将指导您探索许多有趣方向的地方，使用本章作为起点。我们建议您在计算机上跟着本章进行学习，并进行大量的实验、网络搜索和其他必要的工作，以了解发生了什么。在本书的其余部分，您已经积累了足够的技能和专业知识来做到这一点，所以我们相信您会做得很好！

让我们开始手动收集一些数据。

数据

查看untar_data的源代码，看看它是如何工作的。我们将在这里使用它来访问 Imagene 的 160 像素版本，以在本章中使用：

path = untar_data(URLs.IMAGENETTE_160)

要访问图像文件，我们可以使用get_image_files：

t = get_image_files(path)
t[0]

Path('/home/jhoward/.fastai/data/imagenette2-160/val/n03417042/n03417042_3752.JP
 > EG')

或者我们可以使用 Python 的标准库glob来做同样的事情：

from glob import glob
files = L(glob(f'{path}/**/*.JPEG', recursive=True)).map(Path)
files[0]

Path('/home/jhoward/.fastai/data/imagenette2-160/val/n03417042/n03417042_3752.JP
 > EG')

如果您查看get_image_files的源代码，您会发现它使用了 Python 的os.walk；这是一个比glob更快、更灵活的函数，所以一定要尝试一下。

我们可以使用 Python Imaging Library 的Image类打开一张图片：

im = Image.open(files[0])
im

im_t = tensor(im)
im_t.shape

torch.Size([160, 213, 3])

这将成为我们独立变量的基础。对于我们的因变量，我们可以使用pathlib中的Path.parent。首先，我们需要我们的词汇表

lbls = files.map(Self.parent.name()).unique(); lbls

(#10) ['n03417042','n03445777','n03888257','n03394916','n02979186','n03000684','
 > n03425413','n01440764','n03028079','n02102040']

以及反向映射，感谢L.val2idx：

v2i = lbls.val2idx(); v2i

{'n03417042': 0,
 'n03445777': 1,
 'n03888257': 2,
 'n03394916': 3,
 'n02979186': 4,
 'n03000684': 5,
 'n03425413': 6,
 'n01440764': 7,
 'n03028079': 8,
 'n02102040': 9}

这就是我们需要组合成Dataset的所有部分。

数据集

在 PyTorch 中，Dataset可以是任何支持索引（__getitem__）和len的东西：

class Dataset:
    def __init__(self, fns): self.fns=fns
    def __len__(self): return len(self.fns)
    def __getitem__(self, i):
        im = Image.open(self.fns[i]).resize((64,64)).convert('RGB')
        y = v2i[self.fns[i].parent.name]
        return tensor(im).float()/255, tensor(y)

我们需要一个训练和验证文件名列表传递给Dataset.__init__：

train_filt = L(o.parent.parent.name=='train' for o in files)
train,valid = files[train_filt],files[~train_filt]
len(train),len(valid)

(9469, 3925)

现在我们可以尝试一下：

train_ds,valid_ds = Dataset(train),Dataset(valid)
x,y = train_ds[0]
x.shape,y

(torch.Size([64, 64, 3]), tensor(0))

show_image(x, title=lbls[y]);

正如您所看到的，我们的数据集返回独立变量和因变量作为元组，这正是我们需要的。我们需要将这些整合成一个小批量。通常，可以使用torch.stack来完成这个任务，这就是我们将在这里使用的方法：

def collate(idxs, ds):
    xb,yb = zip(*[ds[i] for i in idxs])
    return torch.stack(xb),torch.stack(yb)

这是一个包含两个项目的小批量，用于测试我们的collate：

x,y = collate([1,2], train_ds)
x.shape,y

(torch.Size([2, 64, 64, 3]), tensor([0, 0]))

现在我们有了数据集和一个整合函数，我们准备创建DataLoader。我们将在这里添加两个东西：一个可选的shuffle用于训练集，以及一个ProcessPoolExecutor来并行进行预处理。并行数据加载器非常重要，因为打开和解码 JPEG 图像是一个缓慢的过程。一个 CPU 核心不足以快速解码图像以使现代 GPU 保持繁忙。这是我们的DataLoader类：

class DataLoader:
    def __init__(self, ds, bs=128, shuffle=False, n_workers=1):
        self.ds,self.bs,self.shuffle,self.n_workers = ds,bs,shuffle,n_workers

    def __len__(self): return (len(self.ds)-1)//self.bs+1

    def __iter__(self):
        idxs = L.range(self.ds)
        if self.shuffle: idxs = idxs.shuffle()
        chunks = [idxs[n:n+self.bs] for n in range(0, len(self.ds), self.bs)]
        with ProcessPoolExecutor(self.n_workers) as ex:
            yield from ex.map(collate, chunks, ds=self.ds)

让我们尝试一下我们的训练和验证数据集：

n_workers = min(16, defaults.cpus)
train_dl = DataLoader(train_ds, bs=128, shuffle=True, n_workers=n_workers)
valid_dl = DataLoader(valid_ds, bs=256, shuffle=False, n_workers=n_workers)
xb,yb = first(train_dl)
xb.shape,yb.shape,len(train_dl)

(torch.Size([128, 64, 64, 3]), torch.Size([128]), 74)

这个数据加载器的速度不比 PyTorch 的慢，但它要简单得多。因此，如果您正在调试一个复杂的数据加载过程，不要害怕尝试手动操作，以帮助您准确地了解发生了什么。

对于归一化，我们需要图像统计数据。通常，可以在一个训练小批量上计算这些数据，因为这里不需要精度：

stats = [xb.mean((0,1,2)),xb.std((0,1,2))]
stats

[tensor([0.4544, 0.4453, 0.4141]), tensor([0.2812, 0.2766, 0.2981])]

我们的Normalize类只需要存储这些统计数据并应用它们（要查看为什么需要to_device，请尝试将其注释掉，然后查看后面的笔记本中会发生什么）：

class Normalize:
    def __init__(self, stats): self.stats=stats
    def __call__(self, x):
        if x.device != self.stats[0].device:
            self.stats = to_device(self.stats, x.device)
        return (x-self.stats[0])/self.stats[1]

我们总是喜欢在笔记本中测试我们构建的一切，一旦我们构建它：

norm = Normalize(stats)
def tfm_x(x): return norm(x).permute((0,3,1,2))

t = tfm_x(x)
t.mean((0,2,3)),t.std((0,2,3))

(tensor([0.3732, 0.4907, 0.5633]), tensor([1.0212, 1.0311, 1.0131]))

这里tfm_x不仅仅应用Normalize，还将轴顺序从NHWC排列为NCHW（如果你需要提醒这些首字母缩写指的是什么，请参阅第十三章）。PIL 使用HWC轴顺序，我们不能在 PyTorch 中使用，因此需要这个permute。

这就是我们模型的数据所需的全部内容。现在我们需要模型本身！

Module 和 Parameter

要创建一个模型，我们需要Module。要创建Module，我们需要Parameter，所以让我们从那里开始。回想一下，在第八章中我们说Parameter类“没有添加任何功能（除了自动调用requires_grad_）。它只用作一个‘标记’，以显示要包含在parameters中的内容。”这里有一个确切的定义：

class Parameter(Tensor):
    def __new__(self, x): return Tensor._make_subclass(Parameter, x, True)
    def __init__(self, *args, **kwargs): self.requires_grad_()

这里的实现有点尴尬：我们必须定义特殊的__new__ Python 方法，并使用内部的 PyTorch 方法_make_subclass，因为在撰写本文时，PyTorch 否则无法正确处理这种子类化或提供官方支持的 API 来执行此操作。也许在你阅读本文时，这个问题已经得到解决，所以请查看本书网站以获取更新的详细信息。

我们的Parameter现在表现得就像一个张量，正如我们所希望的：

Parameter(tensor(3.))

tensor(3., requires_grad=True)

现在我们有了这个，我们可以定义Module：

class Module:
    def __init__(self):
        self.hook,self.params,self.children,self._training = None,[],[],False

    def register_parameters(self, *ps): self.params += ps
    def register_modules   (self, *ms): self.children += ms

    @property
    def training(self): return self._training
    @training.setter
    def training(self,v):
        self._training = v
        for m in self.children: m.training=v

    def parameters(self):
        return self.params + sum([m.parameters() for m in self.children], [])

    def __setattr__(self,k,v):
        super().__setattr__(k,v)
        if isinstance(v,Parameter): self.register_parameters(v)
        if isinstance(v,Module):    self.register_modules(v)

    def __call__(self, *args, **kwargs):
        res = self.forward(*args, **kwargs)
        if self.hook is not None: self.hook(res, args)
        return res

    def cuda(self):
        for p in self.parameters(): p.data = p.data.cuda()

关键功能在parameters的定义中：

self.params + sum([m.parameters() for m in self.children], [])

这意味着我们可以询问任何Module的参数，并且它将返回它们，包括所有子模块（递归地）。但是它是如何知道它的参数是什么的呢？这要归功于实现 Python 的特殊__setattr__方法，每当 Python 在类上设置属性时，它就会为我们调用。我们的实现包括这一行：

if isinstance(v,Parameter): self.register_parameters(v)

正如你所看到的，这是我们将新的Parameter类用作“标记”的地方——任何属于这个类的东西都会被添加到我们的params中。

Python 的__call__允许我们定义当我们的对象被视为函数时会发生什么；我们只需调用forward（这里不存在，所以子类需要添加）。在我们这样做之前，如果定义了钩子，我们将调用一个钩子。现在你可以看到 PyTorch 的钩子并没有做任何花哨的事情——它们只是调用任何已注册的钩子。

除了这些功能之外，我们的Module还提供了cuda和training属性，我们很快会用到。

现在我们可以创建我们的第一个Module，即ConvLayer：

class ConvLayer(Module):
    def __init__(self, ni, nf, stride=1, bias=True, act=True):
        super().__init__()
        self.w = Parameter(torch.zeros(nf,ni,3,3))
        self.b = Parameter(torch.zeros(nf)) if bias else None
        self.act,self.stride = act,stride
        init = nn.init.kaiming_normal_ if act else nn.init.xavier_normal_
        init(self.w)

    def forward(self, x):
        x = F.conv2d(x, self.w, self.b, stride=self.stride, padding=1)
        if self.act: x = F.relu(x)
        return x

我们不是从头开始实现F.conv2d，因为你应该已经在第十七章的问卷中使用unfold完成了这个任务。相反，我们只是创建了一个小类，将它与偏置和权重初始化一起包装起来。让我们检查它是否与Module.parameters正确工作：

l = ConvLayer(3, 4)
len(l.parameters())

并且我们可以调用它（这将导致forward被调用）：

xbt = tfm_x(xb)
r = l(xbt)
r.shape

torch.Size([128, 4, 64, 64])

同样，我们可以实现Linear：

class Linear(Module):
    def __init__(self, ni, nf):
        super().__init__()
        self.w = Parameter(torch.zeros(nf,ni))
        self.b = Parameter(torch.zeros(nf))
        nn.init.xavier_normal_(self.w)

    def forward(self, x): return [email protected]() + self.b

测试一下是否有效：

l = Linear(4,2)
r = l(torch.ones(3,4))
r.shape

torch.Size([3, 2])

让我们也创建一个测试模块来检查，如果我们将多个参数作为属性包含，它们是否都被正确注册：

class T(Module):
    def __init__(self):
        super().__init__()
        self.c,self.l = ConvLayer(3,4),Linear(4,2)

由于我们有一个卷积层和一个线性层，每个层都有权重和偏置，我们期望总共有四个参数：

t = T()
len(t.parameters())

我们还应该发现，在这个类上调用cuda会将所有这些参数放在 GPU 上：

t.cuda()
t.l.w.device

device(type='cuda', index=5)

现在我们可以使用这些部分来创建一个 CNN。

简单的 CNN

正如我们所见，Sequential类使许多架构更容易实现，所以让我们创建一个：

class Sequential(Module):
    def __init__(self, *layers):
        super().__init__()
        self.layers = layers
        self.register_modules(*layers)

    def forward(self, x):
        for l in self.layers: x = l(x)
        return x

这里的forward方法只是依次调用每个层。请注意，我们必须使用我们在Module中定义的register_modules方法，否则layers的内容不会出现在parameters中。

所有的代码都在这里

请记住，我们在这里没有使用任何 PyTorch 模块的功能；我们正在自己定义一切。所以如果你不确定register_modules做什么，或者为什么需要它，再看看我们为Module编写的代码！

我们可以创建一个简化的AdaptivePool，它只处理到 1×1 输出的池化，并且也将其展平，只需使用mean：

class AdaptivePool(Module):
    def forward(self, x): return x.mean((2,3))

这就足够我们创建一个 CNN 了！

def simple_cnn():
    return Sequential(
        ConvLayer(3 ,16 ,stride=2), #32
        ConvLayer(16,32 ,stride=2), #16
        ConvLayer(32,64 ,stride=2), # 8
        ConvLayer(64,128,stride=2), # 4
        AdaptivePool(),
        Linear(128, 10)
    )

让我们看看我们的参数是否都被正确注册了：

m = simple_cnn()
len(m.parameters())

现在我们可以尝试添加一个钩子。请注意，我们在Module中只留了一个钩子的空间；您可以将其变成列表，或者使用类似Pipeline的东西将几个钩子作为单个函数运行：

def print_stats(outp, inp): print (outp.mean().item(),outp.std().item())
for i in range(4): m.layers[i].hook = print_stats

r = m(xbt)
r.shape

0.5239089727401733 0.8776043057441711
0.43470510840415955 0.8347987532615662
0.4357188045978546 0.7621666193008423
0.46562111377716064 0.7416611313819885
torch.Size([128, 10])

我们有数据和模型。现在我们需要一个损失函数。

损失

我们已经看到如何定义“负对数似然”：

def nll(input, target): return -input[range(target.shape[0]), target].mean()

实际上，这里没有对数，因为我们使用与 PyTorch 相同的定义。这意味着我们需要将对数与 softmax 放在一起：

def log_softmax(x): return (x.exp()/(x.exp().sum(-1,keepdim=True))).log()

sm = log_softmax(r); sm[0][0]

tensor(-1.2790, grad_fn=<SelectBackward>)

将这些结合起来就得到了我们的交叉熵损失：

loss = nll(sm, yb)
loss

tensor(2.5666, grad_fn=<NegBackward>)

请注意公式

$log (\frac{a}{b}) = log (a) - log (b)$

在计算对数 softmax 时，这给出了一个简化，之前定义为(x.exp()/(x.exp().sum(-1))).log()：

def log_softmax(x): return x - x.exp().sum(-1,keepdim=True).log()
sm = log_softmax(r); sm[0][0]

tensor(-1.2790, grad_fn=<SelectBackward>)

然后，有一种更稳定的计算指数和的对数的方法，称为LogSumExp技巧。这个想法是使用以下公式

$log 左括号 sigma-求和下标 j 等于 1 上标 n 上标 e 上标 x 上标 j 下标基准右括号等于 log 左括号 e 上标 a 基准 sigma-求和下标 j 等于 1 上标 n 上标 e 上标 x 上标 j 下标减 a 基准右括号等于 a 加 log 左括号 sigma-求和下标 j 等于 1 上标 n 上标 e 上标 x 上标 j 下标减 a 基准右括号$

其中a是 $x_{j}$ 的最大值。

以下是相同的代码：

x = torch.rand(5)
a = x.max()
x.exp().sum().log() == a + (x-a).exp().sum().log()

tensor(True)

我们将其放入一个函数中

def logsumexp(x):
    m = x.max(-1)[0]
    return m + (x-m[:,None]).exp().sum(-1).log()

logsumexp(r)[0]

tensor(3.9784, grad_fn=<SelectBackward>)

因此我们可以将其用于我们的log_softmax函数：

def log_softmax(x): return x - x.logsumexp(-1,keepdim=True)

这与之前得到的结果相同：

sm = log_softmax(r); sm[0][0]

tensor(-1.2790, grad_fn=<SelectBackward>)

我们可以使用这些来创建交叉熵：

def cross_entropy(preds, yb): return nll(log_softmax(preds), yb).mean()

现在让我们将所有这些部分组合起来创建一个学习者。

学习者

我们有数据、模型和损失函数；在我们可以拟合模型之前，我们只需要另一件事，那就是优化器！这里是 SGD：

class SGD:
    def __init__(self, params, lr, wd=0.): store_attr(self, 'params,lr,wd')
    def step(self):
        for p in self.params:
            p.data -= (p.grad.data + p.data*self.wd) * self.lr
            p.grad.data.zero_()

正如我们在本书中所看到的，有了学习者生活就变得更容易了。学习者需要知道我们的训练和验证集，这意味着我们需要DataLoaders来存储它们。我们不需要任何其他功能，只需要一个地方来存储它们并访问它们：

class DataLoaders:
    def __init__(self, *dls): self.train,self.valid = dls

dls = DataLoaders(train_dl,valid_dl)

现在我们准备创建我们的学习者类：

class Learner:
    def __init__(self, model, dls, loss_func, lr, cbs, opt_func=SGD):
        store_attr(self, 'model,dls,loss_func,lr,cbs,opt_func')
        for cb in cbs: cb.learner = self

    def one_batch(self):
        self('before_batch')
        xb,yb = self.batch
        self.preds = self.model(xb)
        self.loss = self.loss_func(self.preds, yb)
        if self.model.training:
            self.loss.backward()
            self.opt.step()
        self('after_batch')

    def one_epoch(self, train):
        self.model.training = train
        self('before_epoch')
        dl = self.dls.train if train else self.dls.valid
        for self.num,self.batch in enumerate(progress_bar(dl, leave=False)):
            self.one_batch()
        self('after_epoch')

    def fit(self, n_epochs):
        self('before_fit')
        self.opt = self.opt_func(self.model.parameters(), self.lr)
        self.n_epochs = n_epochs
        try:
            for self.epoch in range(n_epochs):
                self.one_epoch(True)
                self.one_epoch(False)
        except CancelFitException: pass
        self('after_fit')

    def __call__(self,name):
        for cb in self.cbs: getattr(cb,name,noop)()

这是我们在本书中创建的最大的类，但每个方法都非常小，所以通过依次查看每个方法，您应该能够理解发生了什么。

我们将调用的主要方法是fit。这个循环

for self.epoch in range(n_epochs)

并在每个 epoch 中分别调用self.one_epoch，然后train=True，然后train=False。然后self.one_epoch对dls.train或dls.valid中的每个批次调用self.one_batch，适当地（在将DataLoader包装在fastprogress.progress_bar之后）。最后，self.one_batch遵循我们在本书中看到的适合一个小批量的一系列步骤。

在每个步骤之前和之后，Learner调用self，self调用__call__（这是标准的 Python 功能）。__call__在self.cbs中的每个回调上使用getattr(cb,name)，这是 Python 的内置函数，返回具有请求名称的属性（在本例中是一个方法）。因此，例如，self('before_fit')将为每个定义了该方法的回调调用cb.before_fit()。

正如您所看到的，Learner实际上只是使用了我们的标准训练循环，只是在适当的时候还调用了回调。所以让我们定义一些回调！

回调

在Learner.__init__中，我们有

for cb in cbs: cb.learner = self

换句话说，每个回调都知道它是在哪个学习器中使用的。这是至关重要的，否则回调无法从学习器中获取信息，或者更改学习器中的内容。因为从学习器中获取信息是如此常见，我们通过将Callback定义为GetAttr的子类，并将默认属性定义为learner，使其更容易：

class Callback(GetAttr): _default='learner'

GetAttr是一个 fastai 类，为您实现了 Python 的标准__getattr__和__dir__方法，因此每当您尝试访问一个不存在的属性时，它会将请求传递给您定义为_default的内容。

例如，我们希望在fit开始时自动将所有模型参数移动到 GPU。我们可以通过将before_fit定义为self.learner.model.cuda来实现这一点；然而，由于learner是默认属性，并且我们让SetupLearnerCB继承自Callback（它继承自GetAttr），我们可以去掉.learner，只需调用self.model.cuda：

class SetupLearnerCB(Callback):
    def before_batch(self):
        xb,yb = to_device(self.batch)
        self.learner.batch = tfm_x(xb),yb

    def before_fit(self): self.model.cuda()

在SetupLearnerCB中，我们还通过调用to_device(self.batch)将每个小批量移动到 GPU（我们也可以使用更长的to_device(self.learner.batch)）。然而，请注意，在self.learner.batch = tfm_x(xb),yb这一行中，我们不能去掉.learner，因为这里我们是设置属性，而不是获取它。

在尝试我们的Learner之前，让我们创建一个回调来跟踪和打印进度。否则，我们将无法真正知道它是否正常工作：

class TrackResults(Callback):
    def before_epoch(self): self.accs,self.losses,self.ns = [],[],[]

    def after_epoch(self):
        n = sum(self.ns)
        print(self.epoch, self.model.training,
              sum(self.losses).item()/n, sum(self.accs).item()/n)

    def after_batch(self):
        xb,yb = self.batch
        acc = (self.preds.argmax(dim=1)==yb).float().sum()
        self.accs.append(acc)
        n = len(xb)
        self.losses.append(self.loss*n)
        self.ns.append(n)

现在我们准备好第一次使用我们的Learner了！

cbs = [SetupLearnerCB(),TrackResults()]
learn = Learner(simple_cnn(), dls, cross_entropy, lr=0.1, cbs=cbs)
learn.fit(1)

0 True 2.1275552130636814 0.2314922378287042

0 False 1.9942575636942674 0.2991082802547771

惊人的是，我们可以用如此少的代码实现 fastai 的Learner中的所有关键思想！现在让我们添加一些学习率调度。

调度学习率

如果我们想要获得良好的结果，我们将需要一个 LR finder 和 1cycle 训练。这两个都是退火回调，也就是说，它们在训练过程中逐渐改变超参数。这是LRFinder：

class LRFinder(Callback):
    def before_fit(self):
        self.losses,self.lrs = [],[]
        self.learner.lr = 1e-6

    def before_batch(self):
        if not self.model.training: return
        self.opt.lr *= 1.2

    def after_batch(self):
        if not self.model.training: return
        if self.opt.lr>10 or torch.isnan(self.loss): raise CancelFitException
        self.losses.append(self.loss.item())
        self.lrs.append(self.opt.lr)

这展示了我们如何使用CancelFitException，它本身是一个空类，仅用于表示异常的类型。您可以在Learner中看到这个异常被捕获。（您应该自己添加和测试CancelBatchException，CancelEpochException等。）让我们尝试一下，将其添加到我们的回调列表中：

lrfind = LRFinder()
learn = Learner(simple_cnn(), dls, cross_entropy, lr=0.1, cbs=cbs+[lrfind])
learn.fit(2)

0 True 2.6336045582954903 0.11014890695955222

0 False 2.230653363853503 0.18318471337579617

并查看结果：

plt.plot(lrfind.lrs[:-2],lrfind.losses[:-2])
plt.xscale('log')

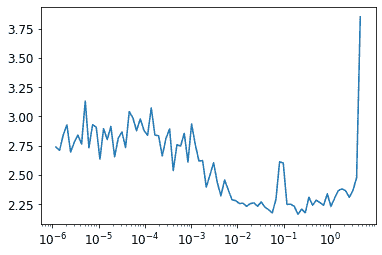
现在我们可以定义我们的OneCycle训练回调：

class OneCycle(Callback):
    def __init__(self, base_lr): self.base_lr = base_lr
    def before_fit(self): self.lrs = []

    def before_batch(self):
        if not self.model.training: return
        n = len(self.dls.train)
        bn = self.epoch*n + self.num
        mn = self.n_epochs*n
        pct = bn/mn
        pct_start,div_start = 0.25,10
        if pct<pct_start:
            pct /= pct_start
            lr = (1-pct)*self.base_lr/div_start + pct*self.base_lr
        else:
            pct = (pct-pct_start)/(1-pct_start)
            lr = (1-pct)*self.base_lr
        self.opt.lr = lr
        self.lrs.append(lr)

我们将尝试一个 LR 为 0.1：

onecyc = OneCycle(0.1)
learn = Learner(simple_cnn(), dls, cross_entropy, lr=0.1, cbs=cbs+[onecyc])

让我们适应一段时间，看看它的样子（我们不会在书中展示所有输出——在笔记本中尝试以查看结果）：

learn.fit(8)

最后，我们将检查学习率是否遵循我们定义的调度（如您所见，我们这里没有使用余弦退火）：

plt.plot(onecyc.lrs);

结论

我们已经通过在本章中重新实现它们来探索 fastai 库的关键概念。由于这本书大部分内容都是代码，您应该尝试通过查看书籍网站上相应的笔记本来进行实验。现在您已经了解了它是如何构建的，作为下一步，请务必查看 fastai 文档中的中级和高级教程，以了解如何自定义库的每一个部分。

问卷调查

实验

对于这里要求您解释函数或类是什么的问题，您还应该完成自己的代码实验。

什么是glob？
如何使用 Python 图像处理库打开图像？
L.map是做什么的？
Self是做什么的？
什么是L.val2idx？
您需要实现哪些方法来创建自己的Dataset？
当我们从 Imagenette 打开图像时为什么要调用convert？
~是做什么的？它如何用于拆分训练和验证集？
~是否适用于L或Tensor类？NumPy 数组、Python 列表或 Pandas DataFrames 呢？
什么是ProcessPoolExecutor？
L.range(self.ds)是如何工作的？
__iter__是什么？
什么是first？
permute是什么？为什么需要它？
什么是递归函数？它如何帮助我们定义parameters方法？
编写一个递归函数，返回斐波那契数列的前 20 个项目。
什么是super？
为什么Module的子类需要重写forward而不是定义__call__？
在ConvLayer中，为什么init取决于act？
为什么Sequential需要调用register_modules？
编写一个打印每个层激活形状的钩子。
什么是 LogSumExp？
为什么log_softmax有用？
什么是GetAttr？它如何帮助回调？
重新实现本章中的一个回调，而不继承自Callback或GetAttr。
Learner.__call__是做什么的？
什么是getattr？（注意与GetAttr的大小写区别！）
在fit中为什么有一个try块？
为什么在one_batch中检查model.training？
什么是store_attr？
TrackResults.before_epoch的目的是什么？
model.cuda是做什么的？它是如何工作的？
为什么我们需要在LRFinder和OneCycle中检查model.training？
在OneCycle中使用余弦退火。

进一步研究

从头开始编写resnet18（如有需要，请参考第十四章），并在本章中使用Learner进行训练。
从头开始实现一个批归一化层，并在您的resnet18中使用它。
为本章编写一个 Mixup 回调。
向 SGD 添加动量。
从 fastai（或任何其他库）中挑选几个您感兴趣的特性，并使用本章中创建的对象实现它们。
选择一篇尚未在 fastai 或 PyTorch 中实现的研究论文，并使用本章中创建的对象进行实现。然后：
- 将论文移植到 fastai。
- 向 fastai 提交拉取请求，或创建自己的扩展模块并发布。
提示：您可能会发现使用nbdev来创建和部署您的软件包很有帮助。

标签：__,tensor,self,torch,程序员,FastAI,面向,我们,def
From： https://www.cnblogs.com/apachecn/p/18015482

FastAI 之书（面向程序员的 FastAI）（七）

第四部分：从零开始的深度学习

第十七章：基础神经网络

从头开始构建神经网络层

建模神经元

从头开始的矩阵乘法

逐元素算术

广播

使用标量进行广播

将向量广播到矩阵

广播规则

爱因斯坦求和

前向和后向传递

定义和初始化一个层

梯度和反向传播

Jeremy 说

重构模型

转向 PyTorch

结论

问卷

进一步研究

第十八章：使用 CAM 解释 CNN

CAM 和 Hooks

梯度 CAM

结论

问卷调查

进一步研究

第十九章：从头开始创建一个 fastai 学习器

数据

数据集

Module 和 Parameter

简单的 CNN

所有的代码都在这里

损失

学习者

回调

调度学习率

结论

问卷调查

实验

进一步研究

相关文章

赞助商

阅读排行