标签：ch 不等式 int 差分 约束 leq 算法 顶点

一、题目描述

P5960 【模板】差分约束

---

二、题目简析

差分约束问题的典型特征是一组不等式。只要画出约束图，这类问题都可以准换为最短路径问题。注意：约束图是有向图。

2.1 约束图的顶点

约束图的顶点（\(V\)） = 一个未知数对应一个顶点（\(v_1, v_2, ...,v_n\)） + 一个额外的顶点（\(v_0\)）

2.2 约束图的边

约束图的边由两部分组成：

• 1、从 \(v_0\) 到各顶点的有向边
  有 \(n\) 个顶点，就有 \(n\) 条这样的有向边。同时，这些边的权值为 0。
• 2、由不等式组得到的有向边
  有 \(m\) 个不等式，就有 \(m\) 条这样的有向边。以 \(v_1 - v_2 \leq y_1\) 为例，变形为 \(v_1 \leq v_2 + y_1\)，有向边为 \(e(v_2, v_1)\)，权值为 \(e(v_2, v_1).w = y_1\)。可以总结以下规则：先对不等式变形，使两个顶点位于不等式符号的两侧（顶点前为正符号）；然后，不等式符号开口朝向的顶点为起点，尖端朝向的顶点为终点，权值为开口朝向的那个常数（可正可负）。

举例：
原不等式组：

\[\begin{cases} x_1 - x_2 \leq 3 \\ x_2 - x_3 \leq -2 \\ x_1 - x_3 \leq 1 \end{cases} \]

引入额外顶点 \(v_0\)，并画权值为0的有向边：

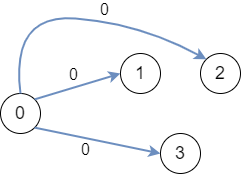
变形：

\[\begin{cases} x_1 \leq x_2 + 3 \\ x_2 \leq x_3 -2 \\ x_1 \leq x_3 + 1 \end{cases} \]

得到最终约束图：

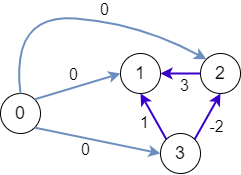
2.3 由约束图求不等式组的解

上文提到，差分约束问题可以用最短路径求解，所以，我们也用一个数组 d[] 记录最短路径。我们令 \(v_0\) 为起点，并初始化为 0。这里，就是 \(d[0] = 0\)。接着，用最短路径算法求 \(v_0\) 到各点的最短路径。各点的最短路径就是不等式组的一个解，即 \(x = (x_1, x_2, ..., x_n) = (d[1], d[2], ..., d[n])\)。
有两点需要注意：

• 1、因为边的权值可能为负，所以只能采用 \(Bellman-Ford\)。若返回 \(ture\)，说明存在负环，所以无解；若返回 \(false\)，说明不存在负环，则有解。
• 2、我们求出的只是不等式组的一个解，有以下性质：
  若 \(x = (x_1, x_2, ..., x_n)\) 是不等式组的解，\(a \in \mathbb{R}\)，则 \(x + a = (x_1 + a, x_2 + a, ..., x_n + a)\) 也是不等式组的解。

---

三、本题代码

#include <bits/stdc++.h>

using namespace std;

#define MAX 5003
#define INF 1e8

typedef struct
{
	int from, to, worth;
} edge;

int n, m;
vector<edge> E;
int d[MAX];

int quickin(void)
{
	int ret = 0;
	bool flag = false;
	char ch = getchar();
	while (ch < '0' || ch > '9')
	{
		if (ch == '-')
			flag = true;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9')
	{
		ret = 10 * ret + ch - '0';
		ch = getchar();
	}
	if (flag)
		ret = -ret;
	return ret;
}

// Bellman-Ford
bool solve(void)
{
	fill(begin(d), end(d), INF);
	d[0] = 0;

	for (int i = 0; i < n; i++)
	{
		bool flag = false;
		for (int j = 0; j < E.size(); j++)
		{
			edge e = E[j];
			if (d[e.from] != INF && d[e.to] > d[e.from] + e.worth)
			{
				d[e.to] = d[e.from] + e.worth;
				flag = true;
				if (i == n - 1)
					return true;	// 存在负环
			}
		}
		if (!flag)
			break;
	}

	return false;
}

int main()
{
	n = quickin(), m = quickin();
	for (int i = 0; i < m; i++)
	{
		int a, b, c;
		a = quickin(), b = quickin(), c = quickin();
		E.push_back(edge{b, a, c});
	}
	// 添加额外点
	for (int i = 1; i <= n; i++)
		E.push_back(edge{0, i, 0});

	if (solve())
		puts("NO");
	else
		for (int i = 1; i <= n; i++)
			printf("%d ", d[i]);

	return 0;
}

---

完

标签：ch,不等式,int,差分,约束,leq,算法,顶点
From： https://www.cnblogs.com/hoyd/p/18011912