原发表于我的博客
贪心算法
贪心与其说是一种算法,不如说一种思想。
贪心思想,顾名思义,就是总是做出当前最好的选择,这种方式可能在全局上不是最好的结果,但是在一些题目中就可以直接用。
最简单的例子就是“货比三家”,在生活中,我们买东西时都会挑性价比最优的,这就是一种贪心。
贪心算法在OI中经常与其他算法或数据结构结合到一起,有些题目比较考验思维能力。
贪心算法一般会用到的算法或数据结构不多,一般的题目只需要用到排序,有些题目可以用优先队列动态维护最值。
接下来我们介绍几种贪心算法的“套路”。
取最优
最经典的问题就是最优装载问题。
商店里有\(n\)个物品,每个物品给出价值和重量,现在来了个小偷,小偷只能带走\(m\)千克的物品,问他最多能带走多少钱的物品。
对于这道题,我们可以直接算出每一个物品的性价比,然后对于性价比排序,依次累加,直到重量超过\(m\)为止。
代码
struct node{
int w,m;//价值和重量
double d;//性价比
}a[N];
bool cmp(node a,node b){
return a.d>b.d;//按照性价比从小到大排序
}
int n,m;
int main(){
cin>>n>>m;//n个物品,限定m重量
for(int i=1;i<=n;i++) cin>>a[i].w>>a[i].m,a[i].d=(double)a[i].w/(double)a[i].m;
sort(a+1,a+1+n,cmp);//排序
int s1=0,s2=0;//分别为价值的累计和重量的累计
for(int i=1;i<=n;i++){
s1+=a[i].w,s2+=a[i].m;
if(s2+a[i+1].m>m) break;//如果超出m限制,就退出
}
cout<<s1;//输出累计价格
}
不相交区间问题
在一个数轴上有n条线段,现要选取其中k条线段使得这k条线段两两没有重合部分,问最大的k为多少?
关于这题的贪心策略,我们可以按每个区间的右端点排序,然后每个区间判断一下是否与前面的区间重合,累加答案即可。
代码
struct node{
int l,r;//结构体
};
vector<node>v;
int n,ans=0;
bool cmp(node a,node b){
return a.r<b.r;//按右端点排序
}
int main(){
cin>>n;
while(n--){
int l,r;
cin>>l>>r;
v.push_back({l,r});//使用vector容器
}
sort(v.begin(),v.end(),cmp);
int l=v.front().l;//初始l为第一个区间的左端点
for(auto it:v){
if(it.l>=l){//如果不重合,就累加答案
ans++;
l=it.r;//更新l指针
}
}
cout<<ans;
}
区间选点问题
给定\(N\)个区间\([a,b]\),取尽量少的点,使得每个区间内都至少有一个点(不同区间内含的点可以重复)。
如何能选取更少的点呢?
如果在几个区间的重叠部分放点,那么就会覆盖多个区间,就会少取一些点。
如图,如果两个区间有重叠部分,那么前面区间的右端点肯定在重叠部分里。
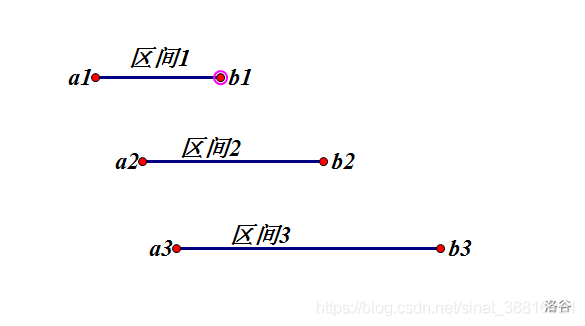
所以我们可以选择在每个区间的右端点放点,这样就会覆盖更少的区间。
所以我们的贪心策略就是:首先按区间的结束位置从小到大排序。然后从区间\(1\)到区间\(n\)进行选择;对于当前区间,若集合中的数不能覆盖它,则将区间末尾的数加入集合。
代码
int vis[N];
struct node{
int u,v,w;
}a[N];
int m,h,ans=0;
int cmp(node a,node b){
return a.v<b.v;//按照右端点排序
}
int main(){
cin>>m>>h;
for(int i=1;i<=h;i++) cin>>a[i].u>>a[i].v>>a[i].w;
sort(a+1,a+1+h,cmp);//排序
for(int i=1;i<=h;i++){
int cnt=0;
for(int j=a[i].u;j<=a[i].v;j++) cnt+=vis[j];
if(cnt>=a[i].w) continue;
for(int j=a[i].v;j>=a[i].u,cnt<a[i].w;j--){
if(!vis[j]) cnt++,vis[j]++,ans++;
}
}
cout<<ans;
}
中位数
在贪心算法中,中位数是一个比较神奇的性质。
我们以经典的货仓选址问题为例。
在一条数轴上有 \(N\) 家商店,它们的坐标分别为 \(A_1∼A_N\)。现在需要在数轴上建立一家货仓,每天清晨,从货仓到每家商店都要运送一车商品。求把货仓建在何处,可以使得货仓到每家商店的距离之和最小。
可以证明,当选取中位数时,距离之和最小。
代码
int a[N],sum,n;
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);
int mid=a[n/2];
for(int i=1;i<=n;i++) sum+=abs(a[i]-mid);
cout<<sum<<endl;
}
与优先队列相结合
很多贪心题目可以和堆结合到一起,在平时做题时,可以使用stl中的优先队列priority_queue。
合并果子是一道比较经典的优先队列优化贪心题。
有\(n\)个果子,每次可以任意选择两个进行合并,每次合并耗费的体力值是两个果子重量之和,问最小耗费体力值。
因为是任意两个进行合并,所以我们可以每次选择果子里面重量最小的两个果子合并。
但是暴力找重量最小的果子复杂度为\(O(n)\),总体\(O(n^2)\)的时间复杂度不能接受。考虑用数据结构优化。
什么数据结构能支持动态找最小值呢?堆!
在这里我们可以使用stl中的优先队列,这样就有了\(O(n\log n)\)的复杂度。
代码
#include<bits/stdc++.h>
using namespace std;
priority_queue<int,vector<int>,greater<int>>q;//优先队列
int n,ans=0;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
int t;
cin>>t;
q.push(t);//在优先队列中加入所有果子
}
while(!q.empty()){
int t1=q.top();//取出当前重量最小的果子
q.pop();
if(q.empty()) break;
int t2=q.top();
q.pop();
ans+=t1+t2,q.push(t1+t2);
}
cout<<ans;
}
反悔贪心
没人看的,所以咕了
例题
一本通提高篇的几道贪心水题。
【一本通提高篇贪心】 活动安排
题目大意
选取最多的区间,使它们没有重叠部分。
贪心思路
按照活动的结束时间进行升序排序,因为一个活动结束的越早,就越不容易与其他活动起冲突。
这题就是上面写到的不相交区间问题,这里就不仔细讲了,直接看代码。
AC代码
#include<bits/stdc++.h>
using namespace std;
const int N=1010;
struct node{
int l,r;//结构体
};
vector<node>v;
int n,ans=0;
bool cmp(node a,node b){
return a.r<b.r;//按右端点排序
}
int main(){
cin>>n;
while(n--){
int l,r;
cin>>l>>r;
v.push_back({l,r});//使用vector容器
}
sort(v.begin(),v.end(),cmp);
int l=v.front().l;//初始l为第一个区间的左端点
for(auto it:v){
if(it.l>=l){//如果不重合,就累加答案
ans++;
l=it.r;//更新l指针
}
}
cout<<ans;
}
【一本通提高篇贪心】 种树
题目大意
即刚刚讲过的区间选点问题。
贪心思路
按每个路段的右端点排序,枚举每一个路段,从左端点枚举到右端点。
因为如果右端点重叠了,就少种了一棵树,所以只要这个位置有树,这个路段要求的树的数量就-1。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=3e4+10;
int vis[N];
struct node{
int u,v,w;
}a[N];
int m,h,ans=0;
int cmp(node a,node b){
return a.v<b.v;
}
int main(){
cin>>m>>h;
for(int i=1;i<=h;i++) cin>>a[i].u>>a[i].v>>a[i].w;
sort(a+1,a+1+h,cmp);
for(int i=1;i<=h;i++){
int cnt=0;
for(int j=a[i].u;j<=a[i].v;j++) cnt+=vis[j];
if(cnt>=a[i].w) continue;
for(int j=a[i].v;j>=a[i].u,cnt<a[i].w;j--){
if(!vis[j]) cnt++,vis[j]++,ans++;
}
}
cout<<ans;
}
【一本通提高篇贪心】 喷水装置
题目大意
有 \(n\) 个浇灌喷头。每个喷头都装在草坪中心线上(离两边各\(\frac{W}{2}\)米)。我们知道每个喷头的位置(离草坪中心线左端的距离),以及它能覆盖到的浇灌范围。
请问:如果要同时浇灌整块草坪,最少需要打开多少个喷头?
贪心思路
这题怎么这么计几啊?
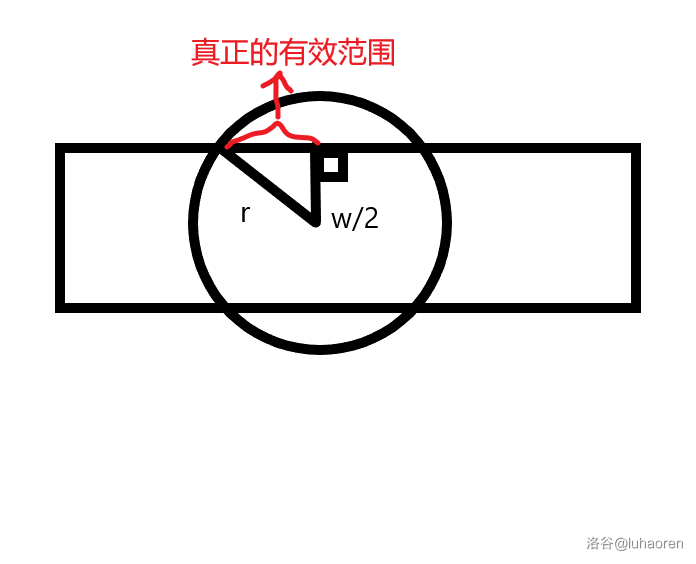
如图,每个喷水装置覆盖的区域不是它的直径,我们需要用勾股定理算出那个圆和那个方块的交集的距离,即\(\sqrt{r^2-(\frac{w}{2})^2}\)。
算出这个距离后,就是一道裸的区间覆盖问题了。
所以我们的贪心思路就是,先处理处每一个区间的左右端点(即\(x-\sqrt{r^2-(\frac{w}{2})^2}\)和\(x+\sqrt{r^2-(\frac{w}{2})^2}\)),然后按左端点排序,依次处理即可,细节部分看代码。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=15010;
int T,n,m;
double l,w;
struct node{
double l,r;
}a[N];
bool cmp(node a,node b){
return a.l<b.l;
}
void work(){
m=0;
cin>>n>>l>>w;
for(int i=1;i<=n;i++){
double id,r;
cin>>id>>r;
if(r<=w/2) continue;
double d=sqrt(r*r-w*w/4.0);
a[++m]={id-d,id+d};
}
sort(a+1,a+1+m,cmp);
double now=0;
int cnt=0,i=1;
while(now<l){
cnt++;
double tmp=now;
while(a[i].l<=tmp&&i<=m) now=max(now,a[i].r),i++;
if(tmp==now&&tmp<l){
cout<<-1<<endl;
return;
}
}
cout<<cnt<<endl;
}
int main(){
cin>>T;
while(T--) work();
return 0;
}
【一本通提高篇贪心】 加工生产调度
题目大意
有\(n\)个物品需要加工,每个物品先在\(A\)车间加工再到\(B\)加工,问最短加工时间。
贪心策略
按每个物品在\(A\)和\(B\)车间的加工时间的最小值排序,然后模拟即可。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1010;
int n;
struct node{
int a,b,id;
}a[N];
int w[N];
bool cmp2(node a,node b){
return min(a.a,b.b)<min(a.b,b.a);
}
bool cmp1(node a,node b){
return min(a.a,a.b)<min(b.a,b.b);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i].a,a[i].id=i;
for(int i=1;i<=n;i++) cin>>a[i].b;
sort(a+1,a+1+n,cmp1);
for(int i=1,l=0,r=n+1;i<=n;i++){
if(a[i].a<a[i].b) w[++l]=a[i].id;
else w[--r]=a[i].id;
}
int s1=0,s2=0;
sort(a+1,a+1+n,cmp2);
for(int i=1;i<=n;i++){
s1+=a[i].a;
s2=max(s1,s2);
s2+=a[i].b;
}
cout<<s2<<endl;
for(int i=1;i<=n;i++) cout<<w[i]<<" ";
}
【一本通提高篇贪心】 智力大冲浪
题目大意
有一些任务,每个任务都有完成期限,完不成一个任务就要扣一些钱,问最多能得到多少钱。
贪心策略
直觉上,如果要扣钱最少,肯定得让扣钱多的排到前面去,然后按照时间依次完成任务。
但是这样做是错误的(通过样例就能得出结论),所以我们需要优化一下这个思路。
我们可以用最优贪心,每个任务都在完成期限的最后一秒完成,用一个数组记录下每个时间点有没有被一个任务占用,然后向前找到最后一个能用的时间即可。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=510;
struct node{
int t,x;
}a[N];
bool cmp(node a,node b){
return a.x>b.x;
}
int n,m,tim[N];
int main(){
cin>>m>>n;
for(int i=1;i<=n;i++) cin>>a[i].t;
for(int i=1;i<=n;i++) cin>>a[i].x;
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++){
for(int j=a[i].t;j;j--){
if(!tim[j]){
tim[j]=1,a[i].x=0;
break;
}
}
}
for(int i=1;i<=n;i++) m-=a[i].x;
cout<<m;
}
【一本通提高篇贪心】 数列极差
题目大意
有\(n\)个正整数,每次删去两个数\(a,b\),放入一个数\(a\times b+1\),问最后得到的一个数的最大值和最小值。
贪心策略
我们会发现这题很像之前的例题果子合并,所以我们可以考虑用堆维护。
而我们要同时维护最大值和最小值,可以用一个大根堆和一个小根堆。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=20;
priority_queue<int,vector<int>,greater<int>>a;//大根堆
priority_queue<int,vector<int>,less<int>>b;//小根堆
int n;
int main(){
cin>>n;
for(int i=1;i<=n;i++){
int t;
cin>>t;
a.push(t),b.push(t);//分别加入两个中
}
//分别进行两个堆的维护过程,具体过程很像果子合并
while(a.size()>1){
int tmp=a.top();
a.pop();
tmp*=a.top();
a.pop();
a.push(tmp+1);
}
while(b.size()>1){
int tmp=b.top();
b.pop();
tmp*=b.top();
b.pop();
b.push(tmp+1);
}
cout<<a.top()-b.top();//输出题目要求维护的极差
}
【一本通提高篇贪心】 数列分段
题目大意
给定的一个正整数数列 ,现要将其分成连续的若干段,并且每段和不超过\(m\),问最少分成几段。
贪心策略
这题就是最简单的贪心了,枚举的过程中累加和,如果超过\(m\)就情况,然后段数\(+1\),没有什么思维含量。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int t,n,m,s=0,cnt=0;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>t;
if(s+t>m) s=0,cnt++;
s+=t;
}
cout<<cnt+1;
}
【一本通提高篇贪心】 线段
题目大意
在一个数轴上有\(n\)条线段,现要选取其中\(k\)条线段使得这\(k\)条线段两两没有重合部分,问最大的\(k\)为多少?
贪心策略
即不相交区间问题,和习题第一道几乎一模一样,这里直接上代码。
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct node{
int l,r;
}a[N];
bool cmp(node a,node b){
return a.r<b.r;
}
int n,k=0;
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) cin>>a[i].l>>a[i].r;
sort(a+1,a+1+n,cmp);
int t=0;
for(int i=1;i<=n;i++){
if(a[i].l>=t) t=a[i].r,k++;
}
cout<<k;
}
【一本通提高篇贪心】 家庭作业
题目大意
有一些作业,每个作业有完成期限,每个作业完成会得到一定的学分,问最多能得到多少学分。
贪心策略
我们会发现这道题和智力大冲浪那题很像,但是那题做法的时间复杂度是\(O(n^2)\),但这题的数据范围是\(10^6\),所以需要优化。
一种优化方式是用并查集优化,并查集数组记录下最远能够追溯到的放置时间,如果用路径压缩优化的话,时间复杂度可以达到\(O(\alpha n)\),其中\(\alpha \le5\)
AC代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+10;
struct node{
int t,x;
}a[N];
bool cmp(node a,node b){
return a.x>b.x;
}
int n,m,tim[N],fa[N],ans=0;
int find(int x){
//并查集查询
if(x==fa[x]) return x;//路径压缩
return fa[x]=find(fa[x]);
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i].t>>a[i].x;
m=max(m,a[i].t);
}
for(int i=0;i<=m;i++) fa[i]=i;//初始化并查集
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;i++){
int d=find(a[i].t);
if(d) fa[d]=d-1,ans+=a[i].x;
}
cout<<ans;
}
【一本通提高篇贪心】 糖果传递
题目大意
有\(n\)个小朋友坐成一圈,每人有\(a_i\)个糖果。每人只能给左右两人传递糖果。每人每次传递一个糖果代价为\(1\)。求使所有人获得均等糖果的最小代价。
贪心策略
本题需要一定的数学推导,比较繁琐,这里暂时略过,读者可以去找网上的题解。
AC代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+10;
int n,a[N],s[N],sum=0;
signed main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i],sum+=a[i];
for(int i=2;i<=n;i++){
s[i]=s[i-1]+a[i]-sum/n;
}
sort(s+1,s+1+n);
int mid=s[n/2+1],ans=0;
for(int i=1;i<=n;i++) ans+=abs(s[i]-mid);
cout<<ans;
}