排序算法
冒泡排序
- 遍历数组
- 每次遍历到的元素和下一个元素比较,如果出现大于下一个,则交换
- 一趟遍历就能使一个元素到它应当出现的地方
图示:
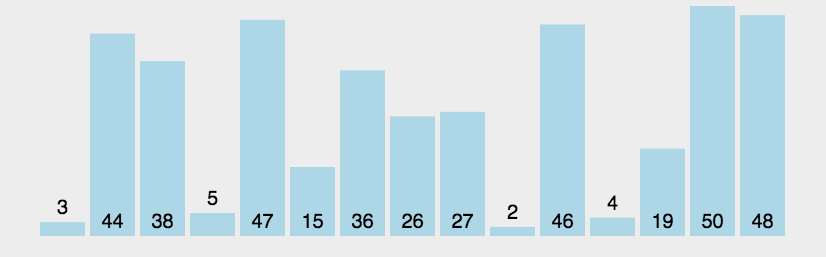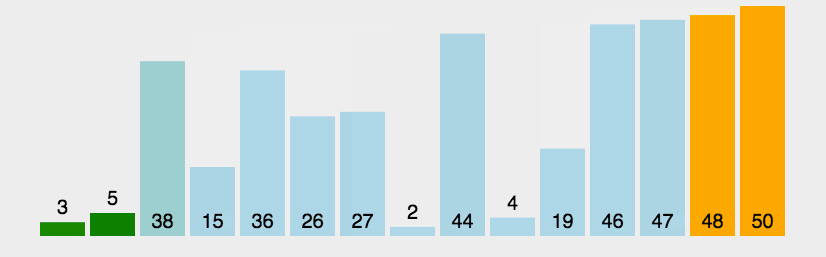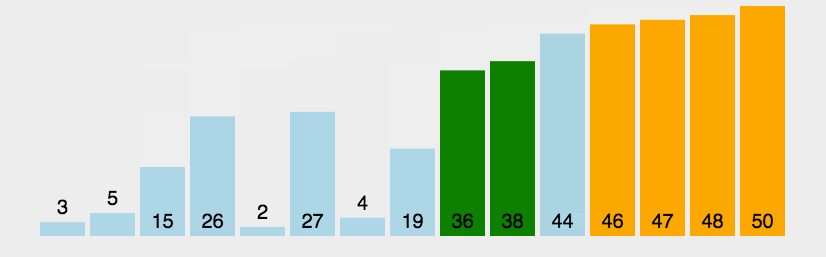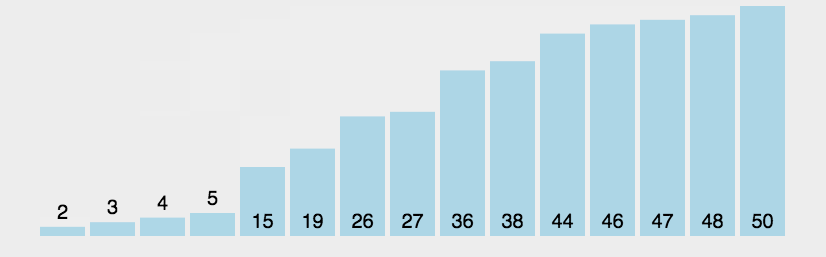
图片源自知乎
代码:
void bubbleSort(int arr[], int n) {
for (int i = 0; i < n - 1; i++) { // 进行n-1轮排序,因为要和下一个比较所以n-1防止越界
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) { // 如果前面的数大于后面的数,则交换位置
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
插入排序
- 第一个元素,我们默认有序
- 取出下一个元素,扫描有序序列,将取出的元素放入有序序列的对应位置
- 重复上一步骤
- 直到最后一个元素也成为有序序列
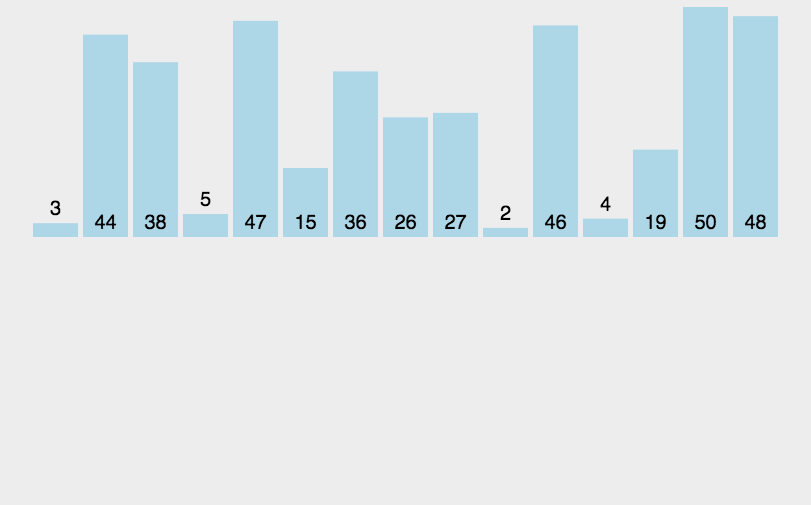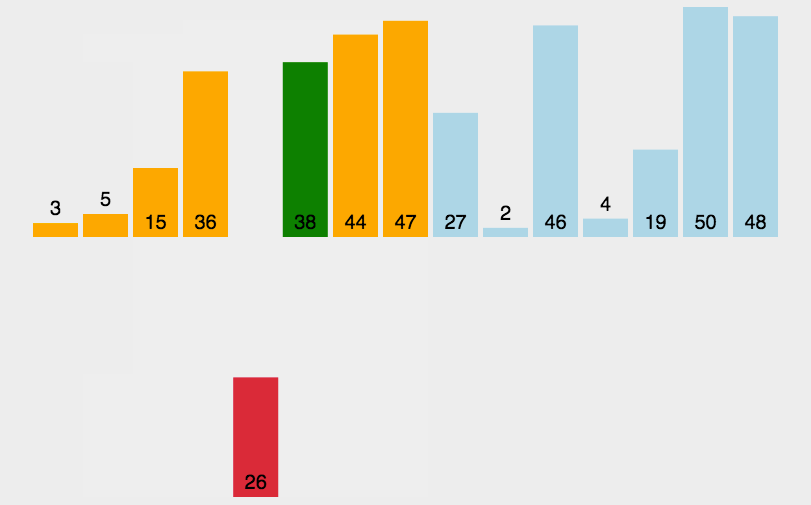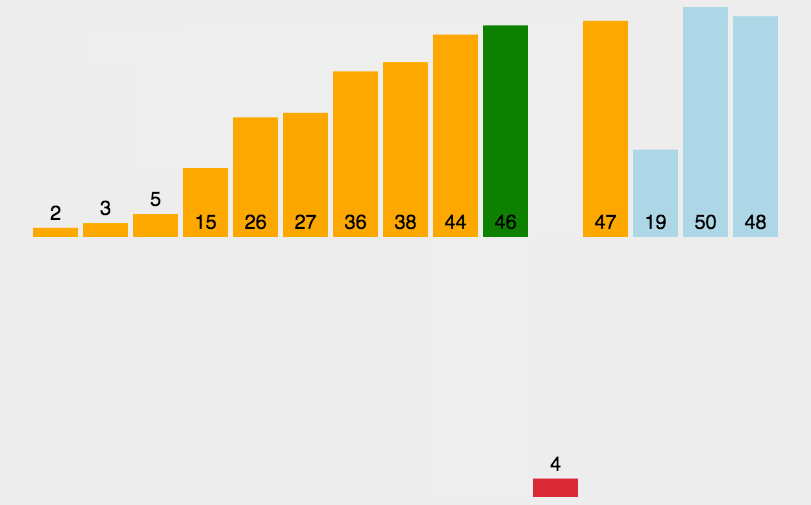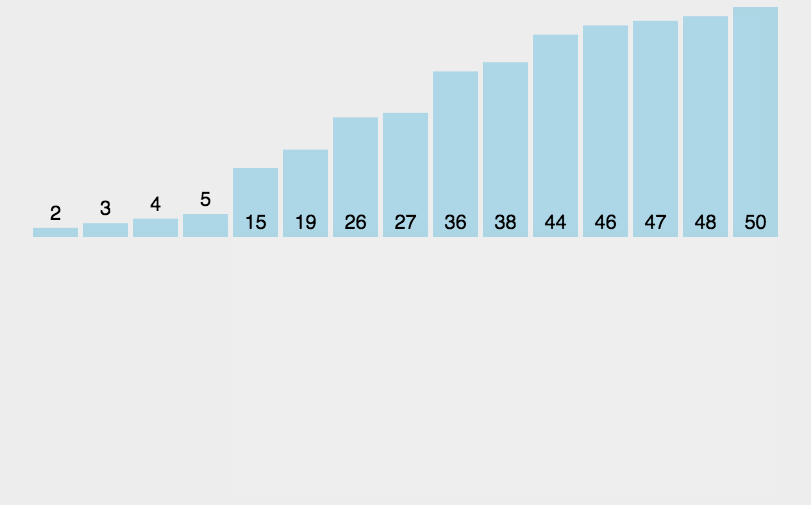
图片源自知乎
代码:
void insertionSort(int *arr,int length){
if( arr==null || length<2 ){
return;
}
for(int i=1; i<length; ++i){//使得0~i有序
//i就是新加入的元素,这个for循环是让有新的元素进来时仍然有序
for(int j=i-1; j>=0 && arr[j]>arr[j+1]; --j){//检查新加入的元素,将其放到合适的位置
//如果a[j]>a[j+1],则进行交换,否则循环停止
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
选择排序
- 遍历数组
- 每次在没有排好序的部分找出当前最大/最小的元素放到排好序的部分对应的位置
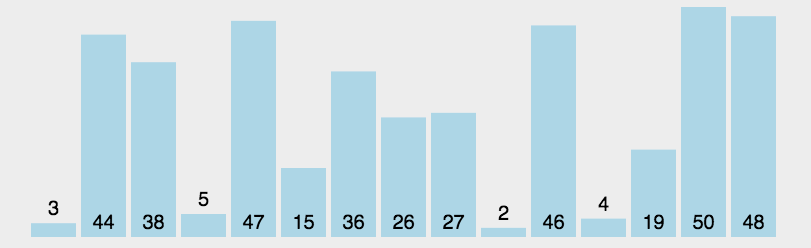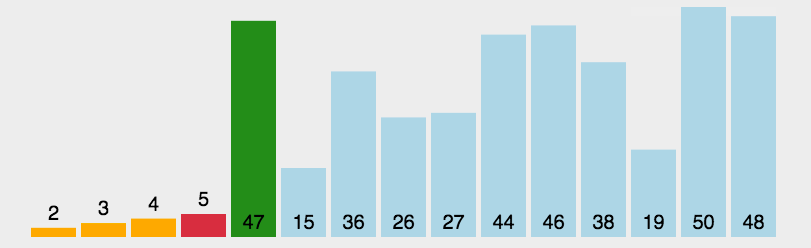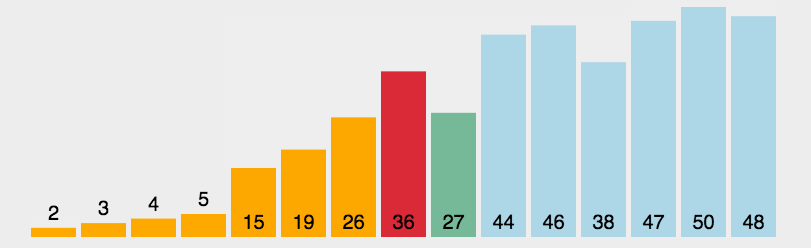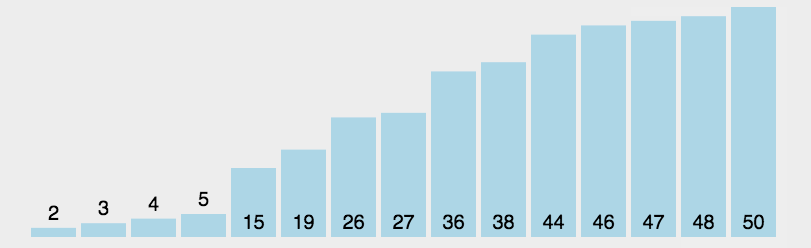
代码:
void selectionSort(int arr[], int n) {
int minIndex = 0;
for (int i = 0; i < n - 1; ++i) {
minIndex = i;
for(int j = i + 1; j < n; ++j){
if (arr[j]<arr[minIndex]){
minIndex = j;
}
}
if(minIndex != i){
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
查找算法
二分
- 有序数组
- 找到
mid position,看mid position和我们要找的数据是不是一样- 防止溢出可以使用`mid = left + ((right - left) >>1 )
- 找的数据更大,就去
mid+1到right中查找 - 找的数据更小,就去
left到mid-1中查找 - 循环要求为
left<right,如果left>right则说明没有符合要求的元素
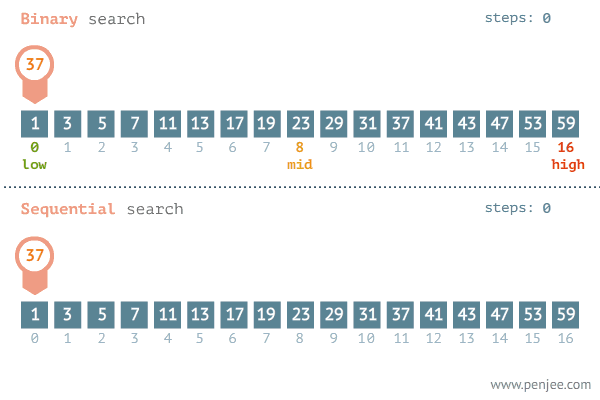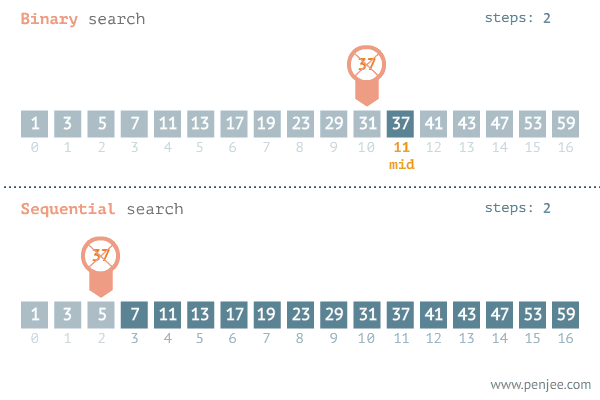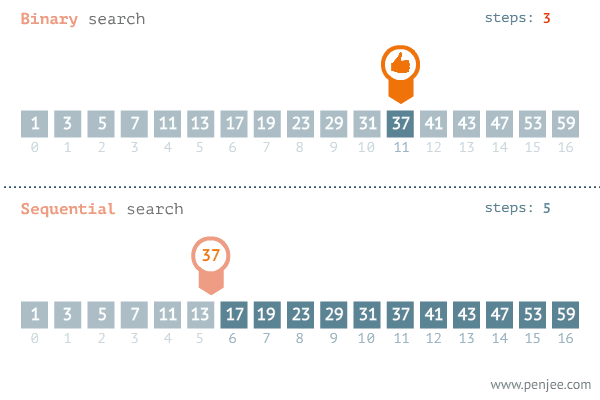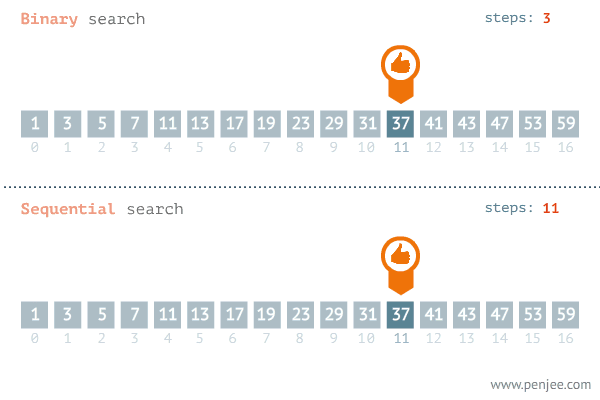
图片源自知乎
int binarySearch(int *arr, int len, int val){
int left = 0, right = len - 1;
int mid = -1;
while(left <= right){
mid = left + ((right - left) >> 1);
if(arr[mid] > val){
right = mid -1;
}else if(arr[mid] < val){
left = mid + 1;
}else{
return mid;
}
}
return -1;
}
int binarySearch(int arr[], int left, int right, int target) {
if (left > right) {
return -1; // 未找到目标元素
}
int mid = left + ((right - left) >> 1);
if (arr[mid] == target) {
return mid; // 找到目标元素
} else if (arr[mid] > target) {
return binarySearch(arr, left, mid - 1, target); // 在左半部分继续查找
} else {
return binarySearch(arr, mid + 1, right, target); // 在右半部分继续查找
}
}
常见的数据结构
堆
其实就是完全二叉树,或者就是从左到右开始的满二叉树
用数组存放完全二叉树,最上面放着最大的元素就是大根堆,放着最小的元素就是小根堆
- 下标为
i的元素,左孩子,如果不为空,则出现在i*2+1下标;右孩子如果不为空,则会出现在i*2+2下标
链表
以节点为单位,节点存储节点信息和下一个节点指针,以指针为连接处将不同节点穿起来
队列
普通队列先进先出;优先级队列底层由大/小根堆实现,先出最大/最小值
哈希表
unorder_set, unorder_map都是哈希表
- 哈希表的增删改查无论数据多大,都是常数操作(比较大的常数,比直接寻址大得多)
树
二叉树的先序、中序、后序遍历
- 先序:先头、再左,最后右
- 中序:先左,再头,最后右
- 后序:先左,再右,最后头
先序遍历
- 将非空节点压栈
- 出栈并打印
- 先将非空右子树节点压栈(空就不压)
- 再将非空左子树节点压栈(空就不压)
- 打印当前栈顶节点
- 重复3,4
std::vector<int> preorderTraversal(TreeNode *root) {
//先序
std::stack<TreeNode *> S;
TreeNode *node;
node = root;
std::vector<int> v;//输出序列
while (node || !S.empty()) {
if (node) {
v.push_back(node->val);//放入输入序列,相当于输出
S.push(node);
node = node->left;
} else {
node = S.top();//当前节点为空,node重新指向父节点然后输出,栈顶此时为最左边的元素
S.pop();
node = node->right;
}
}
return v;
}
std::vector<int> preorderTraversal_(TreeNode *root) {
//先序
std::stack<TreeNode *> S;
TreeNode *node = root;
std::vector<int> V;
S.push(root);
while (!S.empty()) {
node = S.top();
S.pop();
V.push_back(node->val);
if (node->right != nullptr) {
S.push(node->right);
}
if (node->left != nullptr) {
S.push(node->left);
}
}
return V;
}
中序遍历
- 将非空根节点压栈
- 将左节点压栈,直到没有左节点
- 弹栈,打印
- 将弹出的节点的右节点压栈(非空)
- 重复4,5
std::vector<int> inorderTraversal(TreeNode *root) {
//中序
// write code here
std::stack<TreeNode *> S;
TreeNode *node = root;
std::vector<int> V;
while (node || !S.empty()) {
if (node) {
S.push(node);
node = node->left;//从左子树开始,所以先找到最左边的数
} else {
node = S.top();//当节点为空后,此时栈顶为左子树为空的节点,
S.pop();
V.push_back(node->val);
node = node->right;
}
}
return V;
}
后序遍历
和先序遍历有点像
std::vector<int> postorderTraversal(TreeNode *root) {
//后序
std::stack<TreeNode *> S, S1;
TreeNode *node = root;
std::vector<int> V;
S.push(root);
while (!S.empty()) {
node = S.top();
S.pop();
S1.push(node);
if (node->left != nullptr) {
S.push(node->left);
}
if (node->right != nullptr) {
S.push(node->right);
}
}
//输出
while (!S1.empty()) {
V.push_back(S1.top()->val);
S1.pop();
}
return V;
}