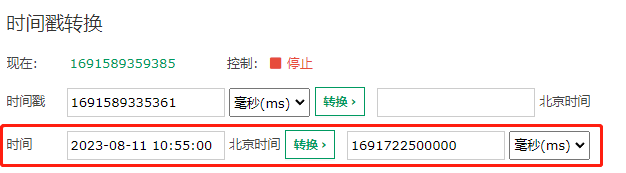
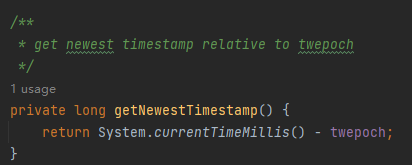
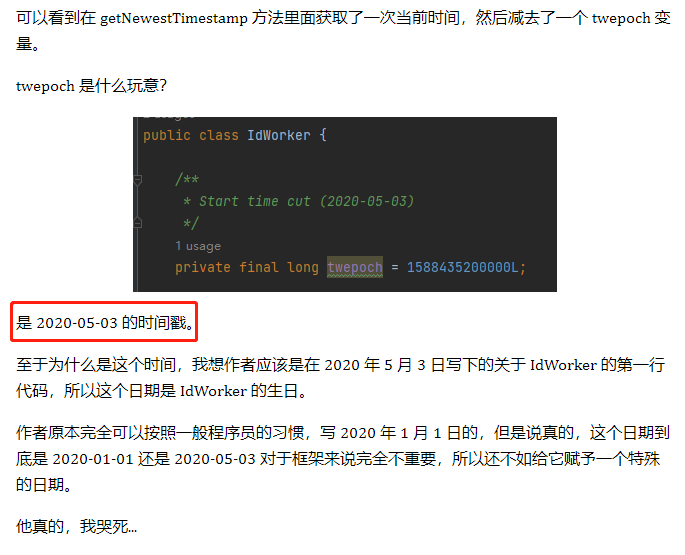
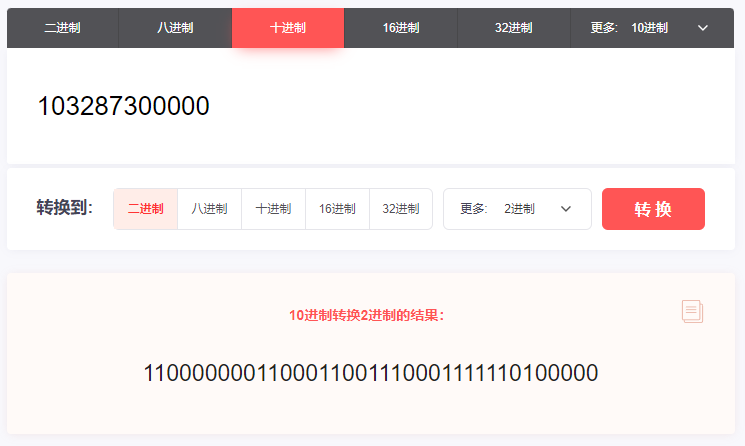
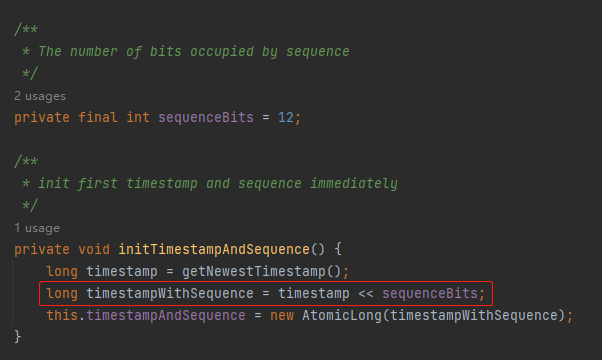
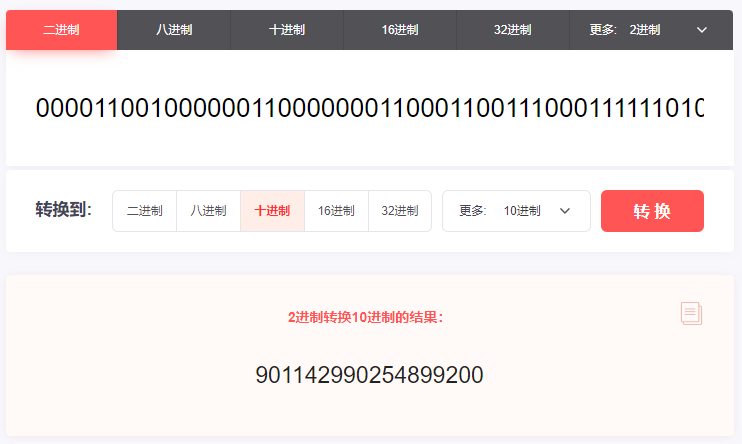
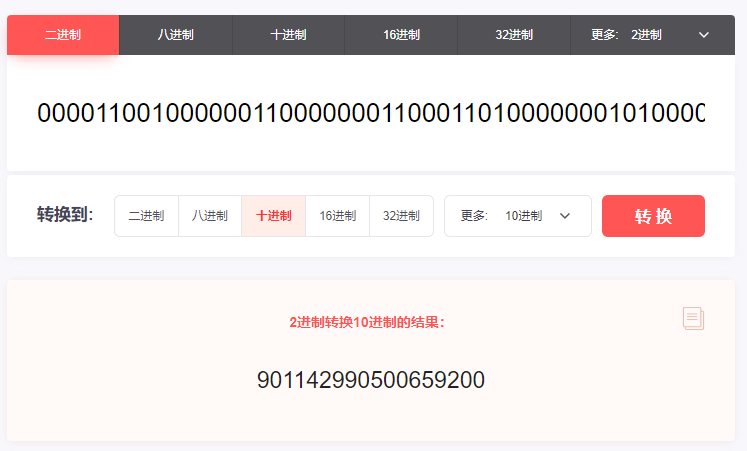
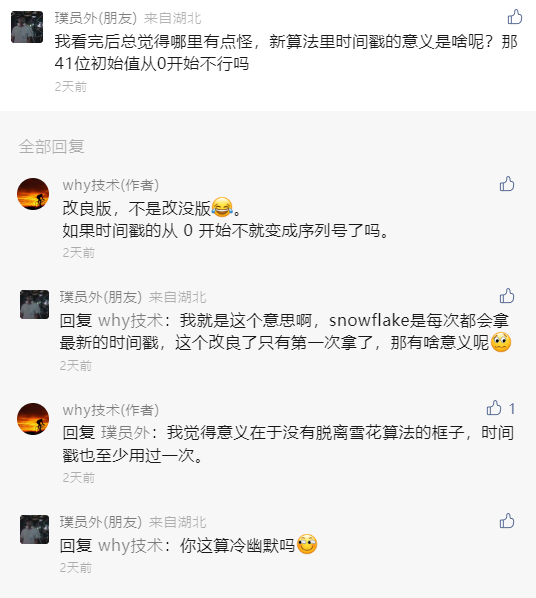
你好呀,我是歪歪。 周一的时候不是发了《在开源项目中看到一个改良版的雪花算法,现在它是你的了。》这篇破文章嘛。 然后有好几个读者都提出了几个类似的问题,再写个续集,给大家解答一下。 我就喜欢这种和读者有来有回,相互拉扯的感觉。 突出一个“相互学习,共同进步。” 首先大家都在纠结的一个点是,文章中提到的超前消费。 我还是把这个改良版本后的图拿过来: 我们先把“超前消费”这个问题框定在一个服务节点上。 假设序列号为 100 的服务节点上的序列号出现了“超前消费”的问题,这个 100 我是随便说的,反正就是代表我们整个系列号的中节点 ID 是固定的。 由于它是固定的,所以在接下来的讨论中,我们并不需要特别关注它。 当我们刨除了“节点ID”之后,那么只剩下 41 位的时间戳和 12 位的序列号: 时间戳在前面的文章中分析过,只是在服务启动的时候会获取一次。 那么我也假设当前的时间戳为 2023 年 08 月 11 日 10 点 55 分 00 秒 000 毫秒。 先说明一下,这个时间戳不考虑人为破坏,修改时区啥的动作,只考虑正常的时间回拨。 你要是考虑人为破坏了,那别玩了,你开玩笑,人心这玩意,是你程序能玩得过的? 好,基于现在的条件,请听题: 基于 Seata 改良版的雪花算法,节点 100 的初始 ID 是多少? 我们完全可以算出来嘛: 首先,第一位恒为 0,就不说了。 然后,节点ID(10位),100 的二进制:1100100。前面补 3 个 0,凑够 10 位,所以就是 0001100100。 接着,时间戳(41位),2023 年 08 月 11 日 10 点 55 分 00 秒 000 毫秒的时间戳为 1691722500000: 1691722500000-1588435200000=103287300000。 有的读者肯定就会问了:这个 1588435200000 是从哪里冒出来的呢? 别问,一问就不是真爱粉了。 前面的文章里面写了: 初始化的时候获取时间戳的代码是这样的: 总之,我们最终算出来的时间戳是 103287300000。 对应的二进制则是这样的: 1100000001100011001110001111110100000 这一串数字一共 37 位,在前面补 4 个 0,凑够 41 位就是这样的: 00001100000001100011001110001111110100000 最后,就是序列号了。 都说了是初始化的时候了,序列号肯定是 0 啊。 所以序列号就是 12 个 0: 000000000000 在程序里面的表现就是把时间戳左移 12 位,把序列号的位置给腾出来。 那么我们最终得到的一个 64 位的二进制就是这样的: 0000110010000001100000001100011001110001111110100000000000000000 歪师傅在给你上个图。 再把这个 64 位的二进制转化为 10 进制,就是这个数: 901142990254899200,就是节点 ID 为 100 的服务器在 2023 年 08 月 11 日 10 点 55 分 00 秒启动瞬间对应的初始化 ID。 听懂掌声。 有的读者肯定要说了:歪师傅,我们不是说超前消费的问题吗? 别急啊,前面不得给你铺垫铺垫,来得太猛我怕你受不了,现在正式说这个超前消费的问题。 现在铺垫完了,那么问题就来了:在我们此时的场景下,出现了什么情况,我们才说这是“超前消费”现象”? 是不是时间戳的最后一位变成了 1 的情况: 因为我们当前的时间是 2023 年 08 月 11 日 10 点 55 分 00 秒 000 毫秒。 但是分布式 ID 生成的时候,时间戳组成部分对应的时间是 2023 年 08 月 11 日 10 点 55 分 00 秒 001 毫秒。 快了 1 毫秒,超前消费 1 毫秒。 那么从程序的角度来看,什么时候会快上这 1ms 呢? 别问,问就不是真爱粉了。 前面的文章说过这个问题了: 就是说在序列号用完了的情况下。 那么序列号怎么才算是用完了呢? 也就是这种情况下,就算用完了: 但是需要注意的是,我们此时的真实时间还是 2023 年 08 月 11 日 10 点 55 分 00 秒 000 毫秒。 意思就是这一毫秒内,序列号从 0 递增到了 4095。 然后还是这一毫秒,还在继续申请 ID,那么序列号归 0,溢出位加到时间戳上,导致时间超前 1ms: 也就是说,只有 QPS 持续稳定在 4096/ms 之上,才有可能出现“超前消费”的情况。 4096/ms,注意我说的是 ms。 换算成秒是 409.6w/s。 QPS 持续稳定在 409.6w/s,你自己啥服务啊,有这么大流量吗,心里没点数? 而且,就算真的有这么大的流量,性能瓶颈一定不是在分布式 ID 生成器这里,前面一定有“高个子”顶着的。 也许你还是觉得看二进制不够直观,那我就给你来个直观的数据,让你感受一小小的震撼。 还是假设当前时间为 2023 年 08 月 11 日 10 点 55 分 00 秒 000 毫秒。 但是程序里面时间“超前消费”了一分钟,对应 2023 年 08 月 11 日 10 点 56 分 00 秒 000 毫秒。 那么按照前面我们的算法,此时对应的 64 位二进制为: 0000110010000001100000001100011010000000101000000000000000000000 对应 10 进制就是其 ID: 901142990500659200 用当前的这个 ID 减去我们之前算出来的 ID: 901142990500659200-901142990254899200=245760000 245,760,000,你自己数一数,2 亿多啊。 如果你想要把时间超前消费 1 分钟,需要持续在 409.6w/s 的流量下申请 2 亿多个流水号。 怎么样,有没有感受到一点点来自数据上的震撼。 所以,这个问题也就顺便回答了读者提出的另外一个问题。 如果当前真实时间是 2023-08 11 10:55:00:000。 而程序持续提前把时间消费到了 2023-08 11 10:56:00:000。 服务重启之后,时间是 2023-08 11 10:55:10:000。 那么由于获取到的时间戳是小于之前“提前消费”的时间戳,就是有可能生成之前重复的 ID。 是的,理论上可能,实际上,不可能会发生。 实际上可能会发生的时什么呢? 瞬时流量达到 4096/ms,出现毫秒级别的时间提前消费。 那么问题就来了:请问你能在毫秒级别完成重启吗? 听懂掌声。 还有一个问的也很多的问题:为什么在改良版本里面,非要把时间戳和节点 ID 换位置,不换行不行? 看到这个问题的时候,我的回复是这样的: 我最开始想到的是,时间戳虽然只是在系统启动的时候获取一次,但是后续由于序列号一轮又一轮的摧残,还是会不断的被 +1。 那么把时间戳放在前面的话,会导致的现象就是时间戳一直在变化,中间的节点 id 又不会变化,会出现递增的时候 id 跨越非常大的情况出现吧。 比如就会出现这种情况: 节点 id 固定,固定的数据在前,id 跨度不会很大,更优雅一点,也就是这样的情况: 但是后来我想明白了,我的说法是错误的,因为在这种生成的 ID 不是单调递增的情况下: 中间跨度很大,很有可能有其他节点生成的序列号。 一旦在出现这种情况,那么就打破了 Seata 关于这次改造的底层设计,即页分裂的次数是有限次的,不考虑页合并的情况下,最多为 1024 次,整个过程最终是收敛的。 也就是这位同学在评论区提到这段话: 如果你看不懂这句话,说明你没看懂我前面发的《在开源项目中看到一个改良版的雪花算法,现在它是你的了。》这篇破文章,可以再瞅一眼。 写到这里的时候,我突然又想明白了另外一个问题: 时间戳的 41 位初始值从 0 开始不行吗? 也就是这样: 我第一次看到这个问题想得是肯定不行,因为这是雪花算法的改良版本,雪花算法的基石就是基于时间,你连时间都不要了,这不是要革了命了吗?而且这样时间戳从 0 开始,那不就变成序列号了吗? 现在我突然想明白这个问题了。 为什么必须要有时间戳? 因为要考虑重启的情况啊。 你想,你第一次启动之后,如果没有时间戳在里面,从 0 开始一直递增,假设递增到了 999。 现在你的服务要重启了,请问,重启之后你的序列号是多少? 你的节点 ID 没变,也没有时间戳,只有个序列号,又没有地方存储重启之前的序列号是多少,那么这次是不是又得从 0 开始了。 哦豁,序列号重复。 谁看了不得说一句:哦豁,宝批龙,瓜起了涩。 啥,你问我“宝批龙”是什么意思? 没啥特别的,类似于“靓仔”。在川渝地区,就是打招呼,问好的一种意思。一般用来形容年轻的帅哥美女。比如你在重庆迷路了,问路的时候你就可以说:嘿宝批龙,你好,请问去朝天门怎么走。 最后,Seata 里面的 IdWorker 类,加上注释一共也才 187 行,源码就在这里,你粘过去就能直接用: https://github.com/seata/seata/blob/2.x/common/src/main/java/io/seata/common/util/IdWorker.java 另外你看文章的时候有没有感到一丝丝奇怪。 为什么我会把当前时间假设为 2023 年 08 月 11 日 10 点 55 分 00 秒 000 毫秒。 这个时间,有零有整的。 因为这个时间是五月天成都演唱会开始抢票的时间: 写篇文章就当许个愿吧,希望我能抢到两张票,和 Max 同学一起去看五月天。 然后,一起唱《干杯》、《突然好想你》、《知足》、《倔强》、《温柔》、《后来的我们》、《恋爱ing》、《志明与春娇》... 一起去找高中时劣质 MP3 中传出的全损音质和在 KTY 时一定要扯着嗓子唱的《噢买尬》和《终结孤单》。 求求了。 好了,如果本文对你有一点点帮助的话,点个免费的赞,求个关注,不过分吧?超前消费













时间戳和节点ID的位置






为什么必须要有时间戳?


代码
