反向传播算法--求偏导速度大大提升（一次求解）

https://zhuanlan.zhihu.com/p/25081671

1 用计算图来解释几种求导方法：

1.1 计算图

式子 e=(a+b)∗(b+1) 可以用如下计算图表达：

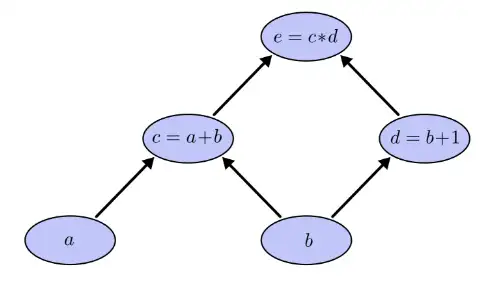
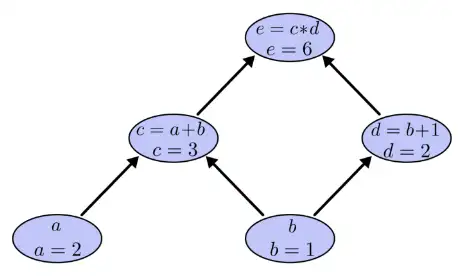
令a=2,b=1则有：

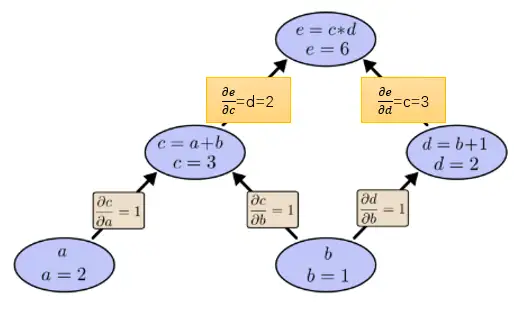
所以上面的求导方法总结为一句话就是： 路径上所有边相乘，所有路径相加。不过这里需要补充一条很有用的合并策略：

1.2 两种求导模式：前向模式求导( forward-mode differentiation) 反向模式求导(reverse-mode differentiation)

上面提到的求导方法都是前向模式求导( forward-mode differentiation) ：从前向后。先求X对Y的总影响 (α+β+γ) 再乘以Y对Z的总影响 (δ+ε+ζ) 。

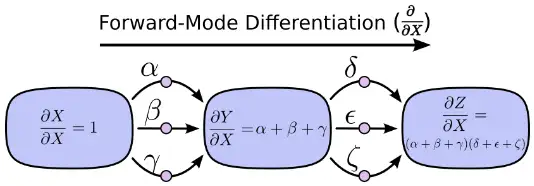
另一种，反向模式求导(reverse-mode differentiation) 则是从后向前。先求Y对Z的影响再乘以X对Y的影响。

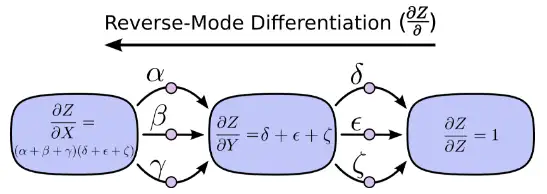
前向求导模式追踪一个输入如何影响每一个节点（对每一个节点进行 ∂/∂X操作）反向求导模式追踪每一个节点如何影响一个输出（对每一个节点进行 ∂Z/∂操作）。

1.3 反向求导模式（反向传播算法）的重要性：

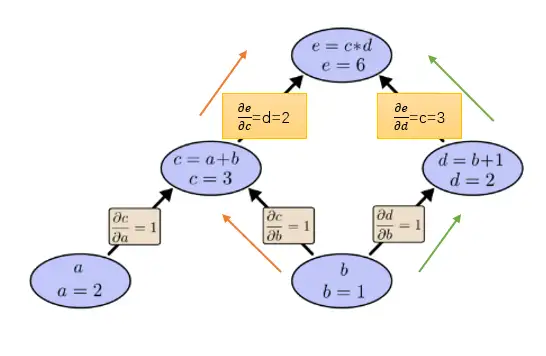
让我们再次考虑前面的例子：

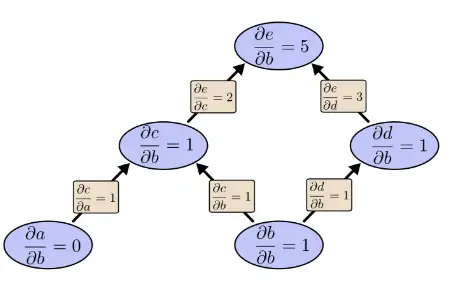
如果用前向求导模式：关于b向前求导一次

如果用反向求导模式：向后求导

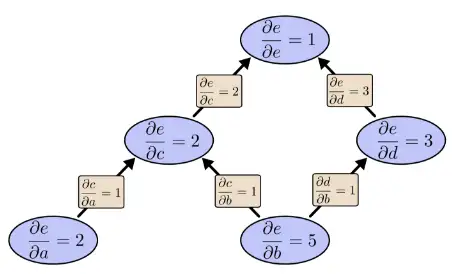
看做门单元之间的运算

https://zhuanlan.zhihu.com/p/21407711

这次计算可以被可视化为如下计算线路图像：

————————————————————————————————————————

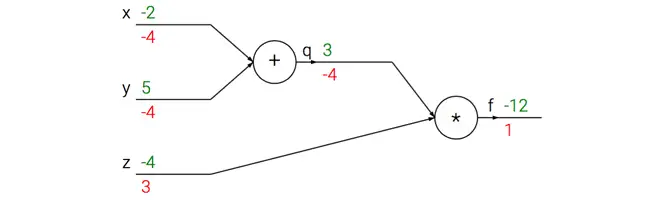
上图的真实值计算线路展示了计算的视觉化过程。前向传播从输入计算到输出（绿色），反向传播从尾部开始，根据链式法则递归地向前计算梯度（显示为红色），一直到网络的输入端。可以认为，梯度是从计算链路中回流。

————————————————————————————————————————

反向传播的直观理解

反向传播是一个优美的局部过程。在整个计算线路图中，每个门单元都会得到一些输入并立即计算两个东西：1. 这个门的输出值，和2.其输出值关于输入值的局部梯度。门单元完成这两件事是完全独立的，它不需要知道计算线路中的其他细节。然而，一旦前向传播完毕，在反向传播的过程中，门单元门将最终获得整个网络的最终输出值在自己的输出值上的梯度。链式法则指出，门单元应该将回传的梯度乘以它对其的输入的局部梯度，从而得到整个网络的输出对该门单元的每个输入值的梯度。

这里对于每个输入的乘法操作是基于链式法则的。该操作让一个相对独立的门单元变成复杂计算线路中不可或缺的一部分，这个复杂计算线路可以是神经网络等。

下面通过例子来对这一过程进行理解。加法门收到了输入[-2, 5]，计算输出是3。既然这个门是加法操作，那么对于两个输入的局部梯度都是+1。网络的其余部分计算出最终值为-12。在反向传播时将递归地使用链式法则，算到加法门（是乘法门的输入）的时候，知道加法门的输出的梯度是-4。如果网络如果想要输出值更高，那么可以认为它会想要加法门的输出更小一点（因为负号），而且还有一个4的倍数。继续递归并对梯度使用链式法则，加法门拿到梯度，然后把这个梯度分别乘到每个输入值的局部梯度（就是让-4乘以x和y的局部梯度，x和y的局部梯度都是1，所以最终都是-4）。可以看到得到了想要的效果：如果x，y减小（它们的梯度为负），那么加法门的输出值减小，这会让乘法门的输出值增大。

因此，反向传播可以看做是门单元之间在通过梯度信号相互通信，只要让它们的输入沿着梯度方向变化，无论它们自己的输出值在何种程度上升或降低，都是为了让整个网络的输出值更高。

回传流中的模式

一个有趣的现象是在多数情况下，反向传播中的梯度可以被很直观地解释。例如神经网络中最常用的加法、乘法和取最大值这三个门单元，它们在反向传播过程中的行为都有非常简单的解释。先看下面这个例子：

——————————————————————————————————————————

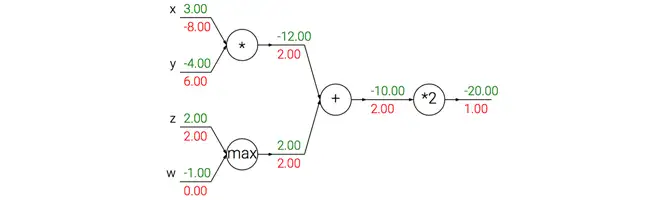一个展示反向传播的例子。加法操作将梯度相等地分发给它的输入。取最大操作将梯度路由给更大的输入。乘法门拿取输入激活数据，对它们进行交换，然后乘以梯度。

——————————————————————————————————————————

从上例可知：

加法门单元把输出的梯度相等地分发给它所有的输入，这一行为与输入值在前向传播时的值无关。这是因为加法操作的局部梯度都是简单的+1，所以所有输入的梯度实际上就等于输出的梯度，因为乘以1.0保持不变。上例中，加法门把梯度2.00不变且相等地路由给了两个输入。

取最大值门单元对梯度做路由。和加法门不同，取最大值门将梯度转给其中一个输入，这个输入是在前向传播中值最大的那个输入。这是因为在取最大值门中，最高值的局部梯度是1.0，其余的是0。上例中，取最大值门将梯度2.00转给了z变量，因为z的值比w高，于是w的梯度保持为0。

乘法门单元相对不容易解释。它的局部梯度就是输入值，但是是相互交换之后的，然后根据链式法则乘以输出值的梯度。上例中，x的梯度是-4.00x2.00=-8.00。

非直观影响及其结果。注意一种比较特殊的情况，如果乘法门单元的其中一个输入非常小，而另一个输入非常大，那么乘法门的操作将会不是那么直观：它将会把大的梯度分配给小的输入，把小的梯度分配给大的输入。在线性分类器中，权重和输入是进行点积W^Tx_i ，这说明输入数据的大小对于权重梯度的大小有影响。例如，在计算过程中对所有输入数据样本 x_i 乘以1000，那么权重的梯度将会增大1000倍，这样就必须降低学习率来弥补。这就是为什么数据预处理关系重大，它即使只是有微小变化，也会产生巨大影响。对于梯度在计算线路中是如何流动的有一个直观的理解，可以帮助读者调试网络。