二分图是一种特殊的图结构,它在经济与管理中具有重要的作用,譬如二分图在市场与供应链管理中发挥着关键作用,在供应链中二分图可以用来描述供应商与分销商之间的关系,帮助确定最佳的供应商-分销商匹配方案。通过建立供应商与分销商之间的连接,可以降低成本、提高效率,并确保产品能够及时、准确地达到市场。在大数据时代,个性化推荐成为了企业吸引客户、提高销售的重要手段。通过建立用户与产品之间的二分图,可以分析用户的偏好、行为模式,并利用推荐算法为用户提供个性化的推荐服务。二分图在广告投放、商品推荐、社交网络分析等方面的应用,为企业提供了更精准、有效的市场营销策略。
一、二分图概述
在经济管理生活中,经常面临双边匹配的问题,比如出行场景中乘客与司机的匹配、物流领域中货物与车辆的匹配、教学领域学生与教师的匹配、营销领域奖励与用户的匹配等。在现实世界稀缺资源约束下(比如人力、物力、财力等),我们希望最终做出的决策达到某种效率的最优,这里的效率可以是时间最少、行驶路程最短、双方满意度等,可以是多种单一指标的综合。
1.1 二分图的界定
二分图,是图论中的一种特殊模型。设\(G=(V,E)\)是一个无向图,如果顶点\(V\)可分割为两个互不相交的子集\((A,B)\),并且图中的每条边\((i,j)\)所关联的两个顶点\(i\)和\(j\)分别属于这两个不同的顶点集(\(iin A,j in B\)),则称图\(G\)为一个二分图。简单来说,如果图中点可以被分为两组,并且使得所有边都跨越组的边界,则这就是一个二分图。准确地说:把一个图的顶点划分为两个不相交子集,使得每一条边都分别连接两个集合中的顶点。如果存在这样的划分,则此图为一个二分图,如下图所示的六个图全都是二分图:

二分图有一个重要的定理:\(G\)为二部图的充要条件是\(G\)中的每一个圈的长度都是偶数。
1.2 匹配问题
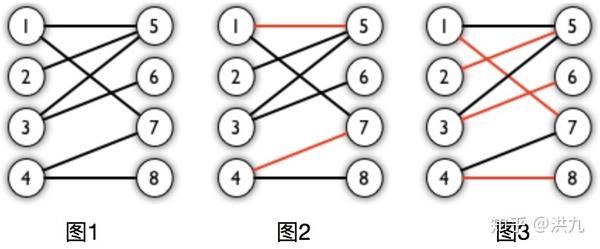
匹配:在图论中,一个匹配(matching)是一个边的集合,其中任意两条边都没有公共顶点。如下图1,图2、图3 中红色的边就是图1的匹配。相关定义还有: 匹配点、匹配边、未匹配点、非匹配边。
事实上,匹配定义中的"其中任意两条边都没有公共顶点"对应了最优化问题形式化中的约束条件,$$\sum_{i=1}^{m}{a_{ij}=1},j=1,2,3... \\ \sum_{j=1}^{n}{a_{ij}=1},i=1,2,3... $$
所以双边匹配最优化问题的本质是从二分图中寻找一个匹配使得目标函数最大。
参看滴滴2018年所发表的论文 《Large-Scale Order Dispatch in On-Demand Ride-Hailing Platforms: A Learning and Planning Approach》中所提及的司乘匹配问题为例,将最优匹配问题建模如下形式:
\[\begin{aligned} & \underset{a_{i j}}{\operatorname{argmax}} \sum_{i=0}^m \sum_{j=0}^n Q_\pi(i, j) a_{i j} \\ & \text { s.t. } \quad \sum_{i=0}^m a_{i j}=1, \quad j=1,2,3 \ldots, n \\ & \sum_{j=0}^n a_{i j}=1, \quad i=1,2,3 \ldots, m \\ & \text { 最优匹配问题形式化定义 } \end{aligned} \]其中, \(a_{i j} \in\{0,1\}\) 表示将乘客 \(i\) 分配给司机 \(j ; Q_\pi(i, j)\) 表示将乘客 \(i\) 分配给司机 \(j\) 的价值(比 如GMV、距离等);约束 \(\sum_{i=1}^m a_{i j}=1, j=1,2,3 \ldots\) 部分的含义为"一个乘客只能分配给至少 且最多一个司机";约束 \(\sum_{j=1}^n a_{i j}=1, i=1,2,3 \ldots\) 部分的含义为"一个司机只能服务至少且 最多一个乘客"。
显然上述问题是一个典型的0-1整数规划问题。忽略具体的业务场景,很大部分的指派问题都可以 建模成如上形式,只是将不同业务诉求隐藏在 \(Q_\pi(i, j)\) 中。
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。上图中图 3 是一个最大匹配,它包含 4 条匹配边。
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。完美匹配一定是最大匹配。
最优匹配:最优匹配又称为带权最大匹配,是指在带有权值边的二分图中,求一个匹配使得匹配边上的权值和最大。一般求最优匹配时,所求二分图的划分 \((U,V)\) 的顶点数相同,使得每一个顶点都需要被匹配,这样也就等同求出了完美匹配。如果\(U\)和 \(V\)的顶点数不同,可以通过补点加权值0边实现转化。
注意最大匹配与最优匹配的区别:
最大匹配不考虑边的权值,即
\[argmax \sum_{i=1}^{n}{\sum_{j=1}^{m}{}a(i,j)} \]最优匹配则考虑了边的权值 \(Q_{\pi}{(i,j)}\) ,即
\[argmax \sum_{i=1}^{n}{\sum_{j=1}^{m}{Q_{\pi}(i,j)}a(i,j)} \]1.3 求解的有关概念
求最大匹配的一种显而易见的算法是:先找出全部的匹配,然后保留匹配数最多的。但是这个算法的时间复杂度是边数的指数级函数。通常更高效的求解二分图最大匹配的算法是匈牙利算法。在介绍匈牙利算法前先了解下交替路和增光路径的概念。
交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边...形成的路径叫交替路。
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路(agumenting path)。如下图(红色边表示已匹配边):
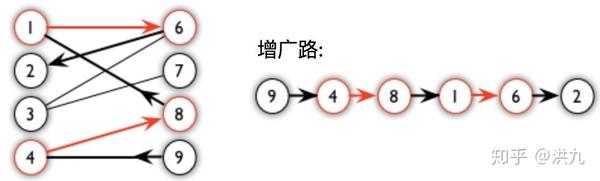
增广路有性质:
(1)增广路经历的节点一定为奇数
(2)增广路中未匹配边比匹配边多"一"。因此我们将增广路取反,也就是"匹配边->未匹配边",同时"未匹配边->匹配边",如此以来匹配边就会增加1。进一步,如果可以不断的找到增广路,则匹配数就会不断递增直到达到最大匹配。
二、二分图求解方法KM
二分图如果是没有权值的,求最大匹配,可以使用用匈牙利算法求最大匹配。如果带了权值,求最大或者最小权匹配(最佳匹配),则必须用KM算法。其实最大和最小权匹配都是一样的问题。只要会求最大匹配,如果要求最小权匹配,则将权值取相反数,再把结果取相反数,那么最小权匹配就求出来了。Kuhn-Munkras(KM)算法用来解决带权二分图最优匹配问题。基本思想是通过引入顶标,将最优权值匹配转化为最大匹配问题。
KM算法流程:
(1)初始化可行顶标的值;
(2)用匈牙利算法寻找完备匹配;
(3)若未找到完备匹配则修改可行顶标的值;
(4)重复(2)(3)直到找到相等子图的完备匹配为止。
[例] 婚姻匹配问题时一个经典的带权二分图问题,现在有\(N\)男\(N\)女,有些男生和女生之间互相有好感,我们将其好感程度定义为好感度,我们希望将他们两两配对,并且最后希望好感度和最大。如何选择最优的配对方法呢?可以使用KM算法求解。
首先,每个女生会有一个期望值,就是与她有好感度的男生中最大的好感度,男生的期望值为0.

接下来开始配对,从第一个女生开始,为她找对象:因为女1+男3=4+0=4,满足“男女两人的期望等于两人之间的好感度”规则。

给女2找对象,因为:女2+男3=3+0=3,满足要求,但是男3已经有对象了,因此给女2找对象失败。接下来需要修改期望值:将发生冲突的女1和女2的期望值降低1,而将冲突源男3的期望值增加1.如此一来女1和男3仍然满足匹配,与男1也满足匹配。女2与男1,男3均满足匹配。修改期望值之后,继续给女2找对象。此时女2-男1匹配,同时女1-男3也匹配。

接下来给女3匹配对象,因为女3+男3=6!=5,因此无法给女3找到匹配。所以让女3的权值减1,此时女3和男3匹配了,但是又和女1冲突了。便去寻找女1,但是对于女1而言可匹配的男1已经和女2 匹配了,于是再去寻找女2。
 而此使对于女2而言,没有其他的边满足匹配规则了,因为现在的寻找路径为:
而此使对于女2而言,没有其他的边满足匹配规则了,因为现在的寻找路径为:
女3->男3->女1->男1->女2,因此需要将左边的女1,2,3结点权值均减去1,将男1,3的权值均加1.

此时对于女1,2,3而言,男1,2,3均已经满足他们的期望值,也就是说现在已经将带权图转换为了无权图。因此接下来的男女匹配问题就可以使用匈牙利算法来实现,下图给出了解。

在这个问题中,冲突一共发生了三次,所以一共降低了3次效率值,但是每次降低的效率值都是最小的,所以完成的仍是最优匹配。这就是KM算法的整个过程。整体思路就是:每次都帮一个顶点匹配最大权重边,利用匈牙利算法完成最大匹配,最终完成的就是最优匹配。
KM算法(Kuhn-Munkres算法),是解决二分图最优匹配问题的经典算法之一。该算法通过不断更新顶标和增广路径来求解最优匹配。它的核心思想是通过增广路径来改变当前匹配,直到找到最优匹配。KM算法的时间复杂度为O(n^3),其中n为二分图中顶点的数量。它具有较高的效率和可靠性,适用于中等规模的二分图最优匹配问题。KM算法在实际应用中具有广泛的意义,在人员分配、任务分配、资源分配等场景中,可以利用KM算法找到最优的匹配方案。在医学影像分析中,可以利用KM算法将病人与适合的诊断器官匹配,提高诊断准确性。在供应链管理中,可以利用KM算法优化供应商与分销商的匹配,提高供应链的效率和盈利能力。
三、二分图最佳匹配Python求解
案例1:问题描述
第二次世界大战时期, 英国皇家空军从沦陷国征募了大量外籍飞行员。 由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的 2 名飞行员, 其中 1 名是英国飞行员,另 1 名是外籍飞行员。 在众多的飞行员中, 每一名外籍飞行员都可以与其他若干名英国飞行员很好地配合。 如何选择配对飞行的飞行员才能使一次派出最多的飞机。 对于给定的外籍飞行员与英国飞行员的配合情况, 试设计一个算法找出最佳飞行员配对方案, 使皇家空军一次能派出最多的飞机。
这是一个二分图匹配问题,【英国飞行员】和【外籍飞行员】可以看作是二分图中两个不相交的点集\(X\),\(Y\)。其中外籍飞行员可以任意与其他若干英国飞行员配合可以看作\(X\)点集中的点有若干条边与\(Y\)中的点相连。每一条相连的边可以看作这两名飞行员能互相配合。求最佳飞行员配对方案,就是求这个二分图的最大匹配。
设有7个英国飞行员,9个外籍飞行员,英国飞行员与外籍飞行员匹配情况如下:
| 英国\ 外籍飞行员 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 |
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 3 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 4 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 |
| 5 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 6 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
class BFS_hungary(object):
def __init__(self, graph):
self.g = graph # 无向图的矩阵表示
self.Nx = len(graph) # 顶点集A的个数
self.Ny = len(graph[0]) # 顶点集B的个数
self.Mx = [-1] * self.Nx # 初始匹配
self.My = [-1] * self.Ny # 初始匹配
self.chk = [-1] * max(self.Nx, self.Ny) # 是否匹配
self.Q = []
def Max_match(self):
res = 0 # 最大匹配数
self.Q = [0 for i in range(self.Nx * self.Ny)]
prev = [0] * max(self.Nx, self.Ny) # 是否访问
for i in range(self.Nx):
if self.Mx[i] == -1: # A中顶点未匹配
qs = qe = 0
self.Q[qe] = i
qe += 1
prev[i] = -1
flag = 0
while (qs < qe and not flag):
u = self.Q[qs]
for v in range(self.Ny):
if flag: continue
if self.g[u][v] and self.chk[v] != i: #
self.chk[v] = i
self.Q[qe] = self.My[v]
qe += 1
if self.My[v] >= 0: #
prev[self.My[v]] = u
else:
flag = 1
d, e = u, v
while d != -1: # 将原匹配的边去掉加入原来不在匹配中的边
t = self.Mx[d]
self.Mx[d] = e
self.My[e] = d
d = prev[d]
e = t
qs += 1
if self.Mx[i] != -1: # 如果已经匹配
res += 1
return res, [x+1 for x in self.Mx], [y+1 for y in self.My]
if __name__ == '__main__':
g = [[1,0,1,0,1,1,1,0,0], [0,1,1,1,0,0,0,1,1], [0,1,0,0,0,1,1,0,0], [1,0,0,0,1,0,1,0,0],
[0,0,0,1,0,0,0,0,1], [1,0,0,0,1,0,0,0,0], [0,0,0,1,0,0,1,0,0], [0,0,0,0,0,0,0,0,0], [0,0,0,0,0,0,0,0,0]]
mm = BFS_hungary(g)
res, Mx, My = mm.Max_match()
print('Maximum matching:', res)
print('Mx:', Mx)
print('My:', My)
Maximum matching: 7
Mx: [3, 2, 6, 5, 4, 1, 7, 0, 0]
My: [6, 2, 1, 4, 5, 3, 7, 0, 0]
案例2:最优匹配
import numpy as np
class KMAlgorithm:
def __init__(self, graph):
self.graph = graph
self.num_girls = len(graph)
self.num_boys = len(graph[0])
self.match = [-1] * self.num_boys
self.visited_girls = [False] * self.num_girls
self.visited_boys = [False] * self.num_boys
self.label_girls = [0] * self.num_girls
self.label_boys = [0] * self.num_boys
def km_algorithm(self):
for i in range(self.num_girls):
while True:
self.visited_girls = [False] * self.num_girls
self.visited_boys = [False] * self.num_boys
if self.dfs(i):
break
delta = float('inf')
for j in range(self.num_girls):
if self.visited_girls[j]:
for k in range(self.num_boys):
if not self.visited_boys[k]:
delta = min(delta, self.label_girls[j] + self.label_boys[k] - self.graph[j][k])
if delta == float('inf'):
return
for j in range(self.num_girls):
if self.visited_girls[j]:
self.label_girls[j] -= delta
for k in range(self.num_boys):
if self.visited_boys[k]:
self.label_boys[k] += delta
def dfs(self, girl):
self.visited_girls[girl] = True
for boy in range(self.num_boys):
if not self.visited_boys[boy] and self.graph[girl][boy] == self.label_girls[girl] + self.label_boys[boy]:
self.visited_boys[boy] = True
if self.match[boy] == -1 or self.dfs(self.match[boy]):
self.match[boy] = girl
return True
return False
# 输入二分图的连接情况
graph=np.array([[3, 5, 2, 1, 6, 4],
[2, 1, 4, 3, 5, 6],
[4, 3, 1, 2, 5, 6],
[6, 1, 2, 3, 5, 4],
[5, 3, 4, 6, 1, 2],
[1, 4, 3, 6, 2, 5]])
# 使用KM算法求解最优匹配
km = KMAlgorithm(graph)
km.km_algorithm()
# 输出最优匹配结果
print("最优匹配方案:")
for boy, girl in enumerate(km.match):
print(f"男孩 {boy+1} 匹配到女孩 {girl+1}")
男孩 1 匹配到女孩 4
男孩 2 匹配到女孩 1
男孩 3 匹配到女孩 2
男孩 4 匹配到女孩 6
男孩 5 匹配到女孩 5
男孩 6 匹配到女孩 3
四、二分图的应用
4.1 二分图最优匹配在师生匹配中的应用
相对完整的数学建模设计应当包含:(1)问题背景 (2)基本假设 (3)基本定义 (4)数学模型 (5)算例分析 几部分。下面以此为顺序详述下二分图最优匹配在研究生录取问题中的应用。
(1)问题背景
硕士研究生的录取目前普遍采用"初试+复试"的方案。一般是根据初试的成绩,在达到国家和学校分数线的学生中从高到低分排序,按1:1.5的比例选择进入复试的名单。复试一般采用由专家组面试考核的办法,主要面试考核学生的专业知识面、思维的创造性、灵活的应变能力、文字和口头的表达能力和外语水平等综合素质。专家组一般由多名专家组成,每位专家根据自己看法和偏好对所有参加复试学生的各个方面都给出相应的评价,可以认为专家组的面试整体评价都是客观的,最后由主管部门综合所有专家的意见和学生的初试成绩等因素确定录取名单。将问题抽象如下:
- 考虑学生的综合评价择优录用,包括初试成绩和面试评价。
- 考虑导师和学生意愿,导师对学生的要求和学生自己的意愿。
- 最优双向选择,一方面每一名导师只带一名学生,同时一名导师可以初选多个学生。
显然,这是一个多目标的最优匹配问题。
(2)基本假设
- 专业方向可以互相调剂.
- 研究生复试专家面试评价及导师学术水平指标的量化。分别把A、B、C、D量化为95,80,70,65;将8个专家的评分取算术平均做为专家对考生的综合评价指标 ;导师学术水平中,每一项所占比例相同,通过标准化处理,令每一项中数值最大者为25分,其余按比例折合。
(3)基本定义
- \(D_{1},D_{2},...,D_{10}\) 代表10名导师
- $S_{1},S_{2},...,S_{15} $代表参加复试的15名学生
(4)数学模型
整个策略分为两部分,首先根据初试成绩和专家评价确定录取同学,其次将录取同学分配给导师。
Part1:确定录取名单
这里采取层次分析法对参加复试的同学打分,最终确定录取的同学。假设结果为:\(S_{1}、S_{2}、S_{3}、S_{4}、S_{5}、S_{6}、S_{7}、S_{8}、S_{9}、S_{12}\)
Part2:双边满意度矩阵
同样参考前面的层次分析法,可以分别建立:
- 10名导师综合水平打分
- 每位学生对每位老师的满意程度,记为\(a_{ki}\),学生 \(K\)对导师 \(i\) 的满意程度
- 每位老师对每位学生的满意程度,记为\(b_{ik}\) ,导师 \(i\) 对学生 \(k\) 的满意程度
Part3:最优匹配模型
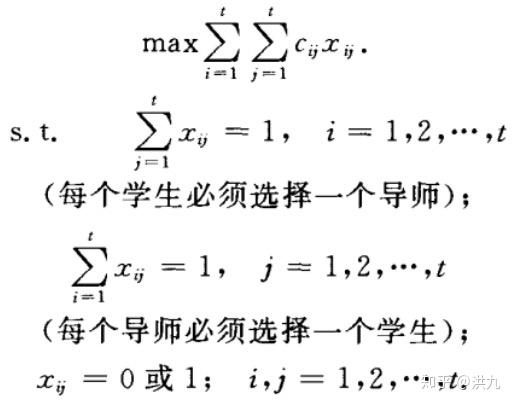
这里的核心是$c_{ij} $的设计。在双边匹配问题中,如果只考虑单边的利益最大化可能会带来很多问题。比如,令 $c_{ik}=b_{ik} $则忽略了学生的诉求,可能会带来严重的师生矛盾,反之亦然。这里令 \(c_{ik}=min(a_{ki},b_{ik})\) ,则同时考虑了导师与学生双边的诉求。
(5)算例分析
这里只给出一个可能的匹配结果:

如果只有5个导师,每个导师带2个学生,该如何处理? 此时可以通过添加虚拟节点的方法解决,也就是将5个导师重复添加。更一般的情况,导师和考生的数目不相等,即当\(M≠N\)时问题的处理。
- 当$N \geq M $时,可以增加 \(N-M\) 位虚拟导师(虚拟结点),虚拟导师对所有考生的满意度均为0, 反之亦然;在匹配方案中,当考生对应的导师为虚拟导师时,该考生即落榜。
- 当 \(N \\leq M\)时,可以增加$M-N $位虚拟考生,任意虚拟考生对导师的满意度为0,反之亦然。
4,2 最小费用最大流模型在指派(分配)问题中的应用
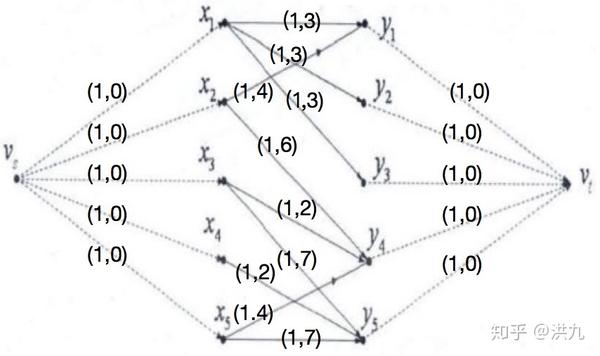
设有5位工程师,5项任务, 他们各自能胜任任务的情况下图所示(边权重代表成本),设计一种任务分配方案,使得尽可能多的工程师分配到任务,并且成本尽可能小的方案。其中\(x_{1}、x_{2}、x_{3}、x_{4}、x_{5}\) 表示工人,$y_{1}、y_{2}、y_{3}、y_{4}、y_{5} $表示任务。
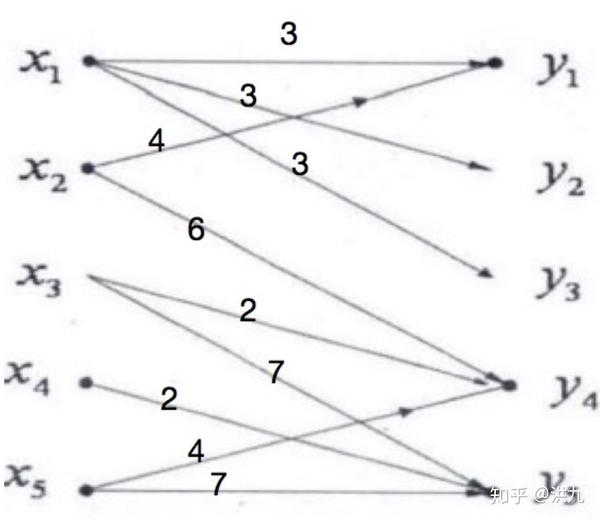
我们可以转化为最小费用最大流问题求解。 在二分图中增加两个新点分别作为发点、收点。并用有向边把它们与原二分图中顶点相连,令全部边上的容量均为1 。最终如下图:
五、总结
随着数据科学和人工智能的不断发展,二分图在解决实际问题和优化决策方面的价值将持续增强。全球供应链网络的复杂性的不断增加,通过建立供应商与分销商之间的二分图模型,可以更好地优化供应链网络、降低成本、提高效率,并实现供应链的可持续发展。金融领域面临着复杂的风险,通过建立金融机构与客户之间的二分图模型,可以更准确地评估风险、制定风险管理策略,并为客户提供个性化的金融产品和服务,提高金融机构的竞争力和稳健性。二分图在经济与管理领域的应用前景广阔。随着技术的不断进步和应用场景的不断扩展,二分图将继续发挥重要作用,为我们提供更精确、高效的决策和优化方案,推动经济与管理的创新和发展。