面试官:写一个堆排吧
堆排是基于堆的一种排序算法,对于堆的了解,请看可以管理时间的二叉堆(如果对堆的插入和删除不清楚,强烈建议先看堆),今天我们聊聊堆排的思想,复杂度以及稳定性
一、堆排思想
前情回顾:慧能给一尘解决了时间管理上的问题[可以管理时间的二叉堆]https://www.iamshuaidi.com/586.html)
过了几天后,一尘高兴地跑到老师跟前


早知不来了,一尘心想

一尘心想:上次去溪边游玩不是已经出过这个题吗,当时学会了冒泡排序,这次肯定不是那么简单,肯定和前几天的堆有关系



一尘:如果将这个数组调整为小根堆,那么根据小根堆堆顶一直是最小元素的特性,我可以不断地取(删除)堆顶的元素,直到堆中只剩下一个元素,这样就可以得到一个递减的元素序列了
删除中交换操作会破坏堆有序,但下沉操作会重新调整堆
一尘画了一个图解释道
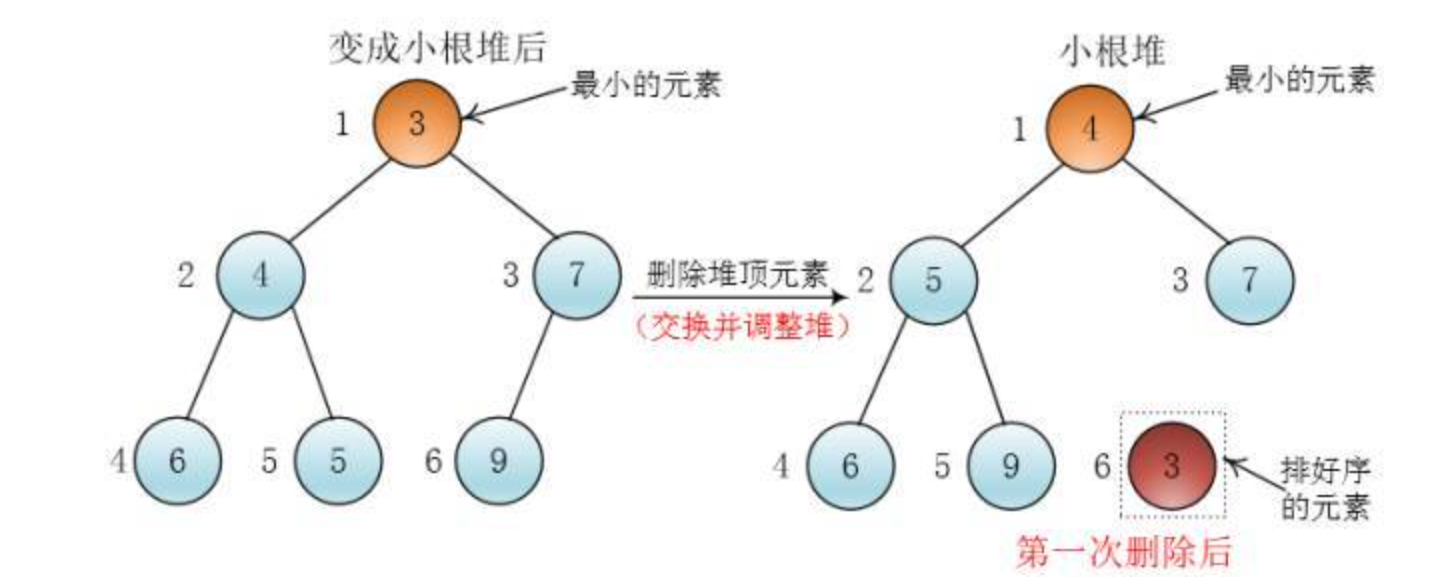

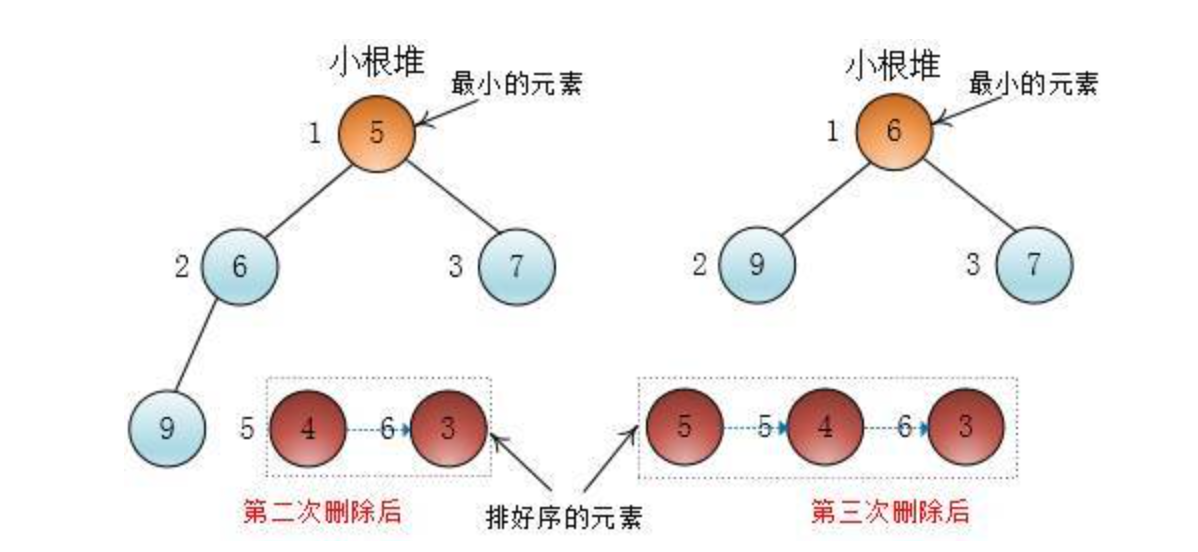

这样一直删除到只有一个元素的时候,整个数组就排好序了
删除包括三个步骤:
① 交换堆顶与堆最后一个元素
② 堆大小(heapSize)减一
③ 调整堆(sink(arr,1))
具体讲解请看:二叉堆

二、建堆

上浮(swim)操作会保持堆有序






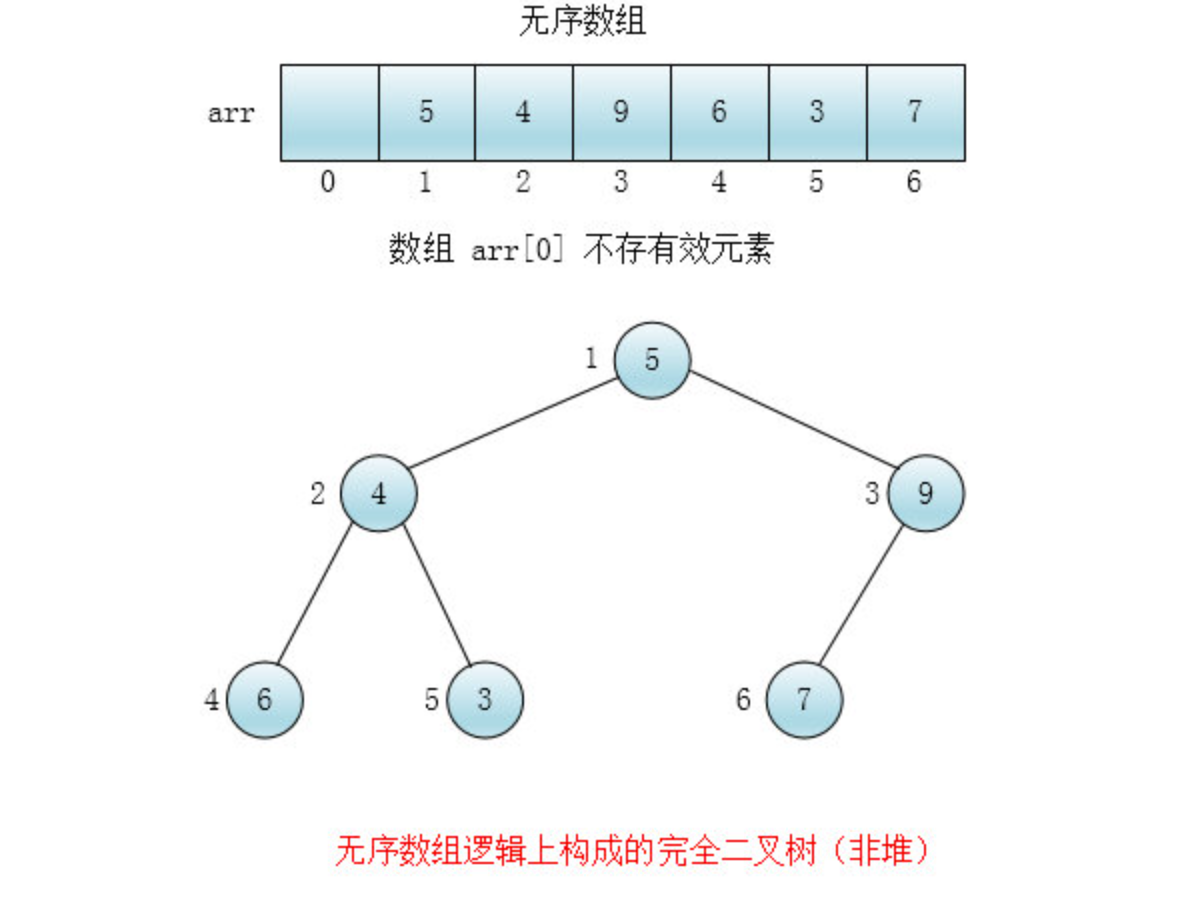

慧能:每个叶子节点可以视为一个大小为一的堆,我们可以自底向上从非叶子节点开始每层从右至左给每个节点都调用下沉(sink)方法,这样以当前节点为根节点的树就变为堆了
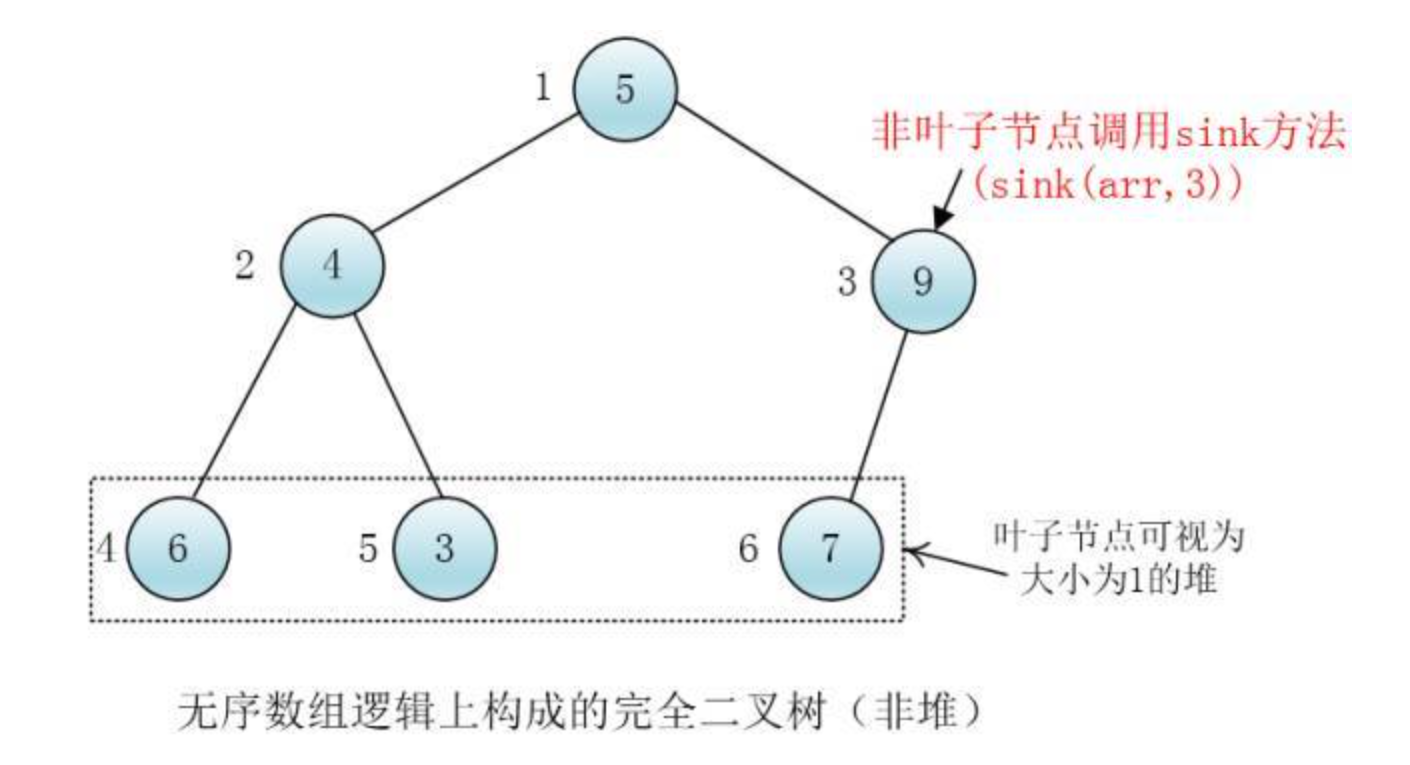
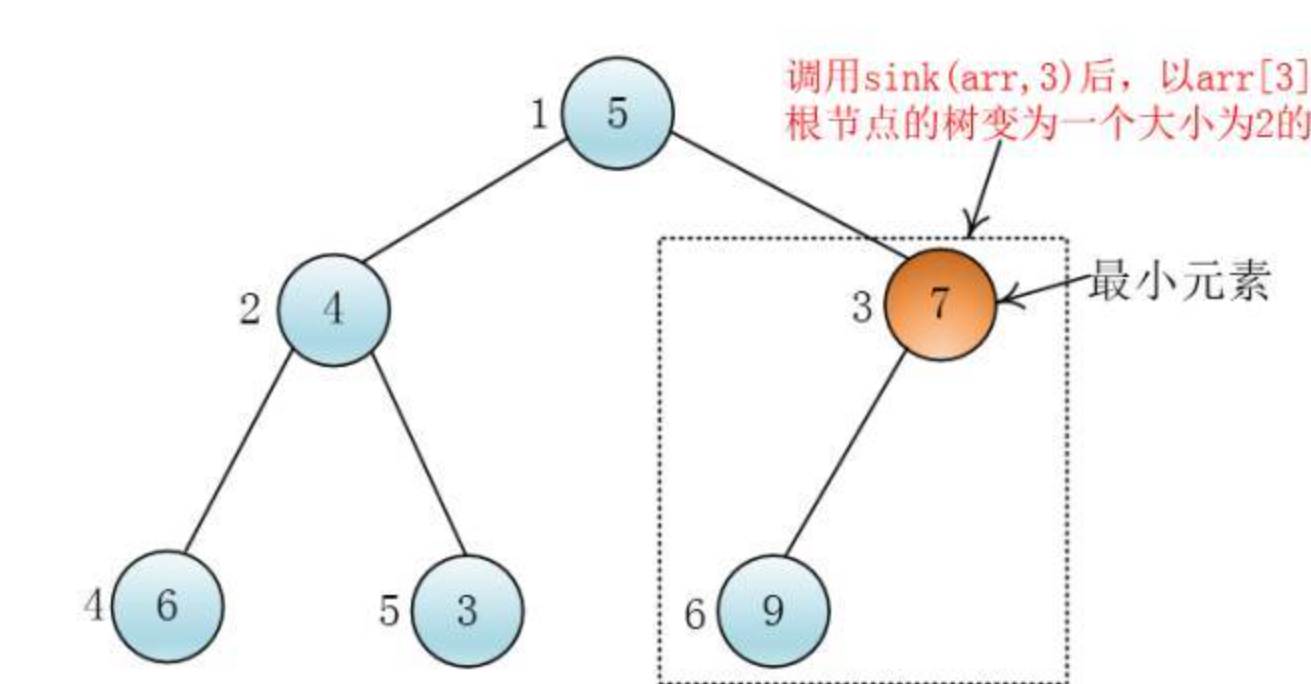

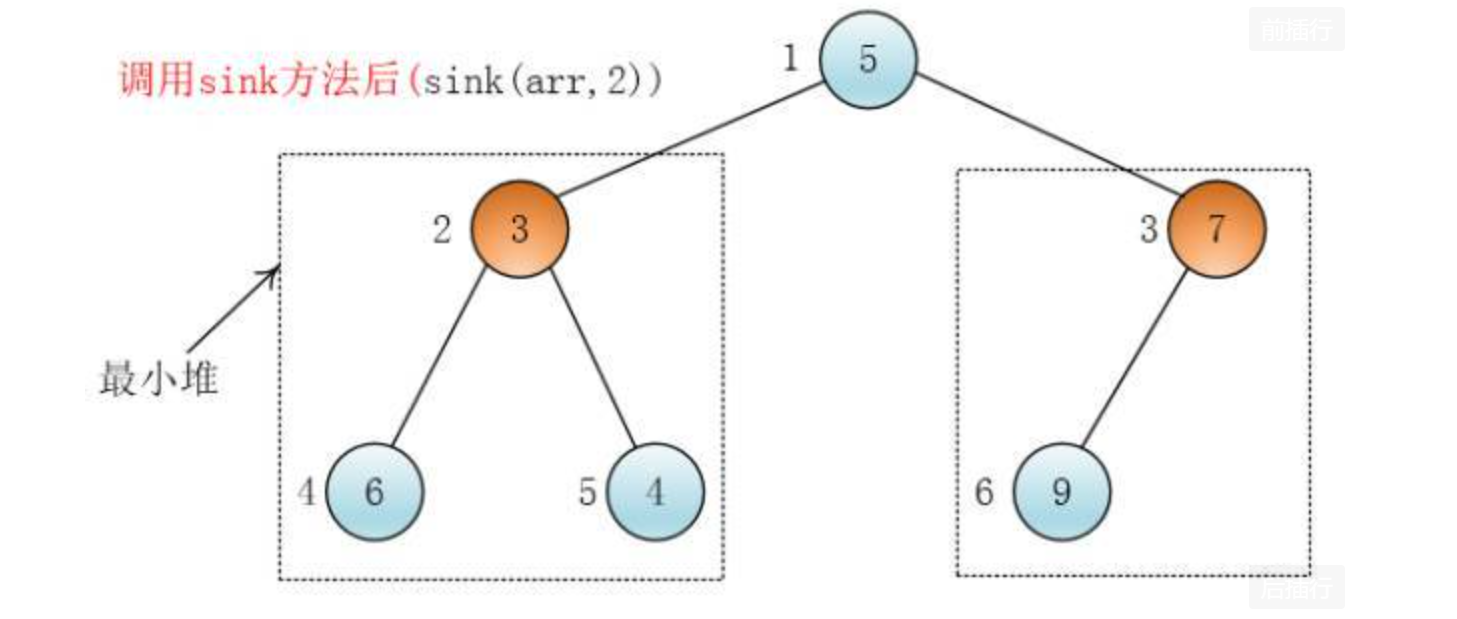

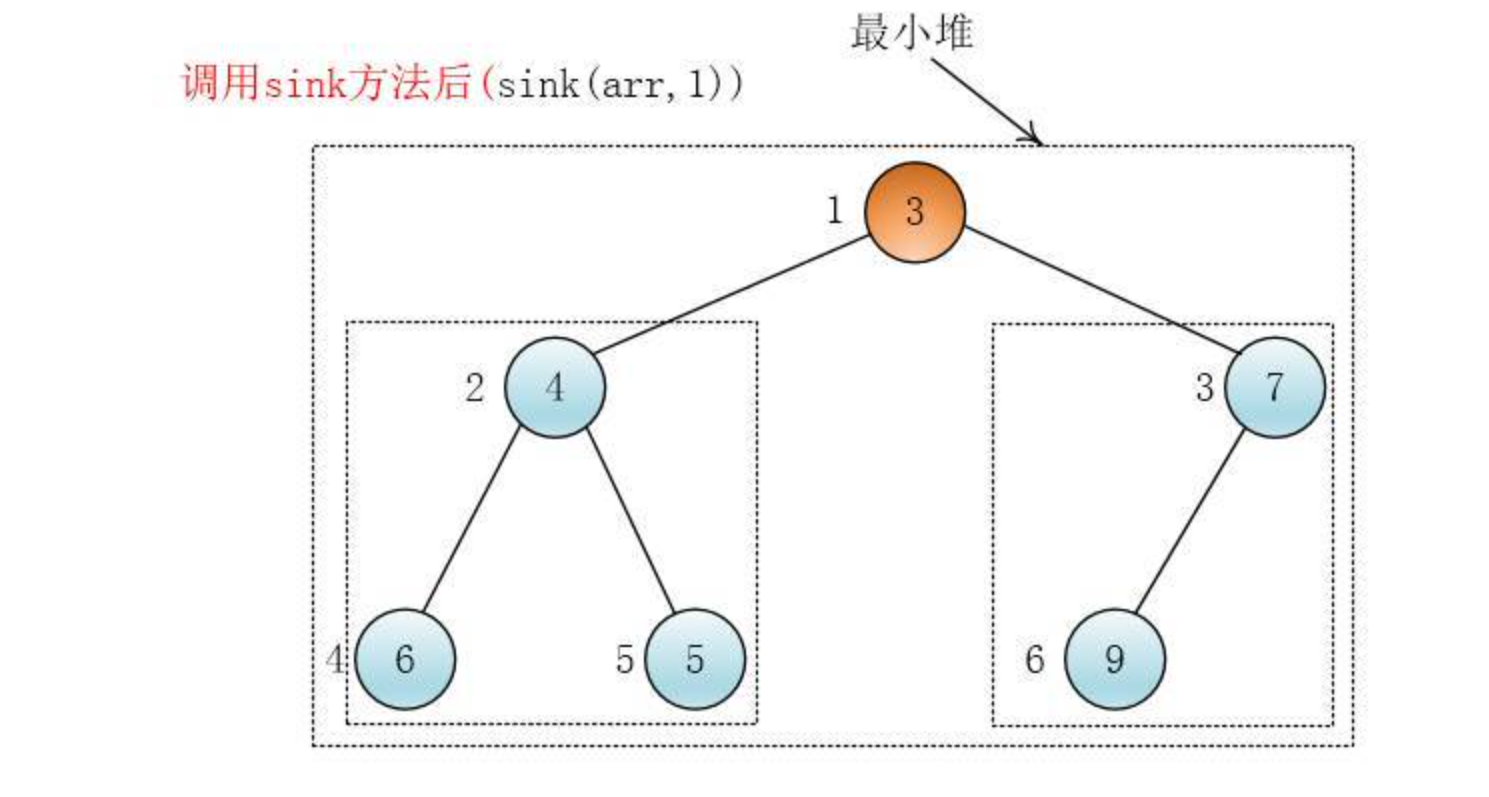

注意:在下沉(sink)某个节点的时候,这个节点的两个孩子必须是堆
三、堆排序代码



又要写代码,一尘心想,虽说心中这样想,但还是要写的,思考了一会,只见一尘写下了如下代码

这里的 heapSize/2 就是第一个非叶子节点的下标
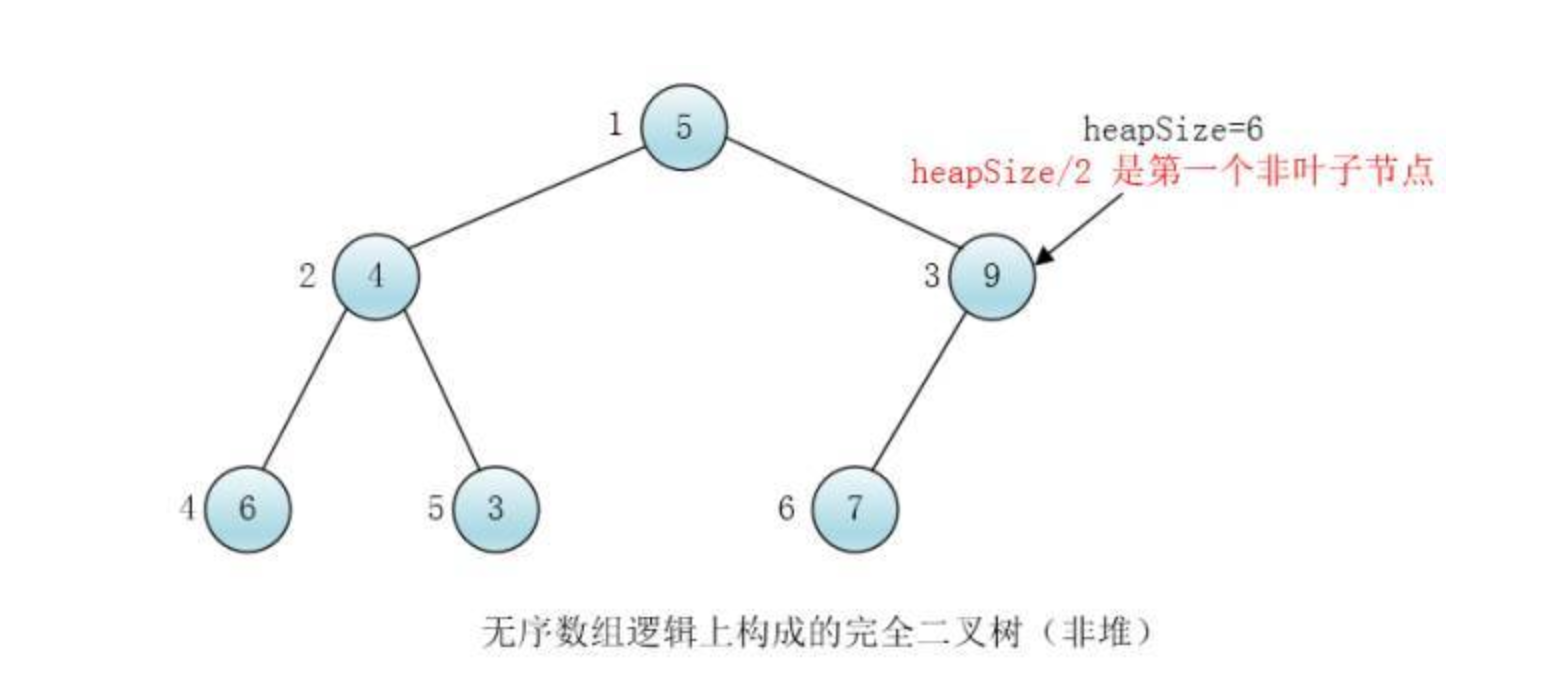
过了一会一尘又写出了删除最小值的代码


前两个都写出来了,剩下的排序就很简单了,按照之前的思路,先建立一个小根堆,然后不断地删除堆顶最小元素,删除N-1次就OK了



一尘暗自惊叹老师的功力,不知不觉又学到了一个排序方法
四、时间复杂度

看到数学头疼的可以直接跳过看结论
一尘还没缓过神,又来了一个最让他头疼的时间复杂度


慧能拿出了笔和纸
慧能:你想一下堆排的整个过程,第一步建堆,第二步执行N-1次deleteMin()方法,最后取两者复杂度较高的就行了
五、建堆时间复杂度
建堆的时候时间消耗在下沉操作上,而下沉操作最多下沉到底,显然,高度为h的节点下沉代价为O(h)
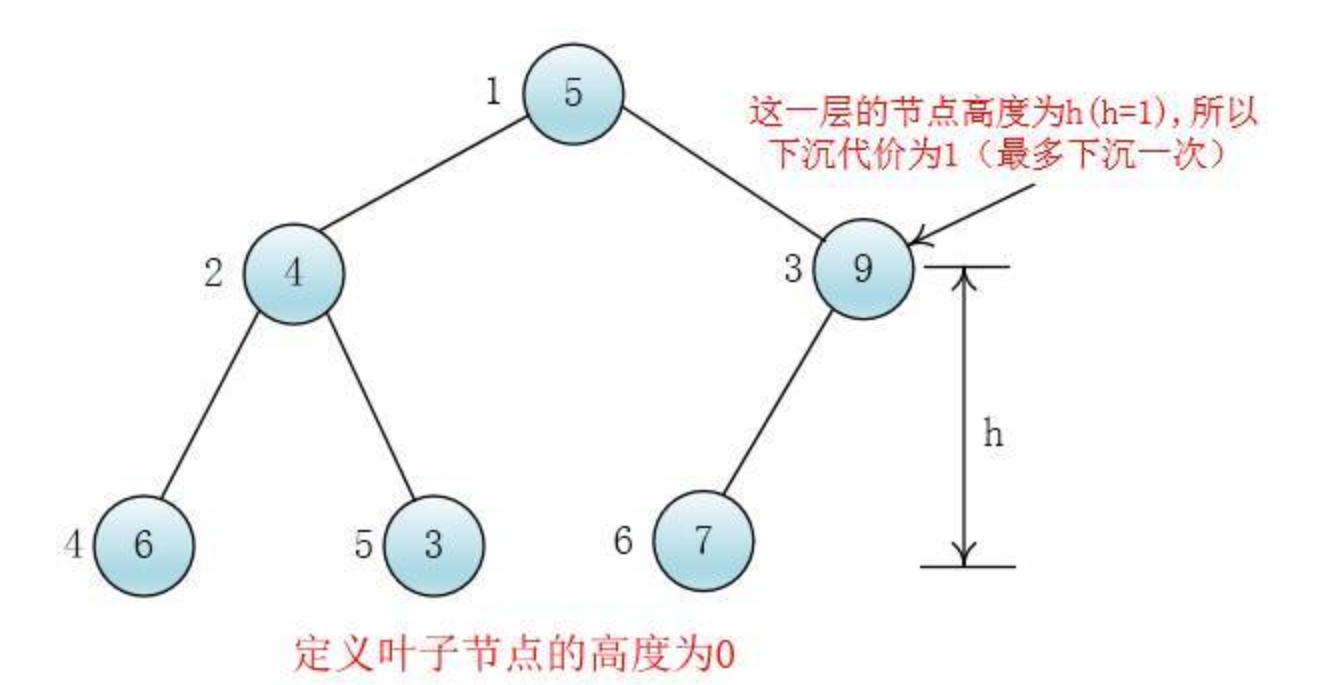
堆中所有元素下沉代价之和就是建堆的代价(时间复杂度)
叶子节点高度为0,下沉代价为0
把堆中不同高度中的所有节点相加起来就是全部的节点
所以问题变为:
① 高度最高多高(高度上界)
② 高度h有多少节点
这里你记住两个结论

有兴趣的可以证证这两个结论
这里我们把不同高度的每个节点执行sink所需要的代价累加起来
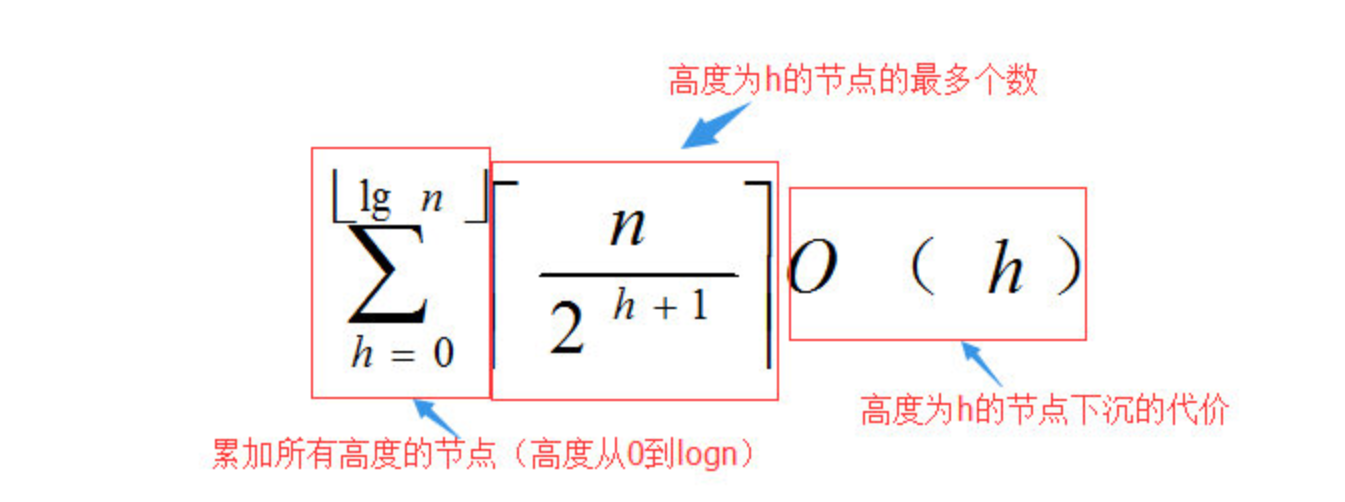



一尘长舒一口气
六、N-1次删除复杂度

n-1次调用deleteMin
deleteMin中包含 swap操作和 sink操作
swap操作代价为常数,sink操作代价为lgn, swap操作相对于sink操作可以忽略不计
则相当于进行了n-1次sink操作
则一共花费的代价为:(n-1)*lgn ~ nlgn
故时间复杂度为O(nlgn)



七、稳定性


一尘说着说着画了一个图
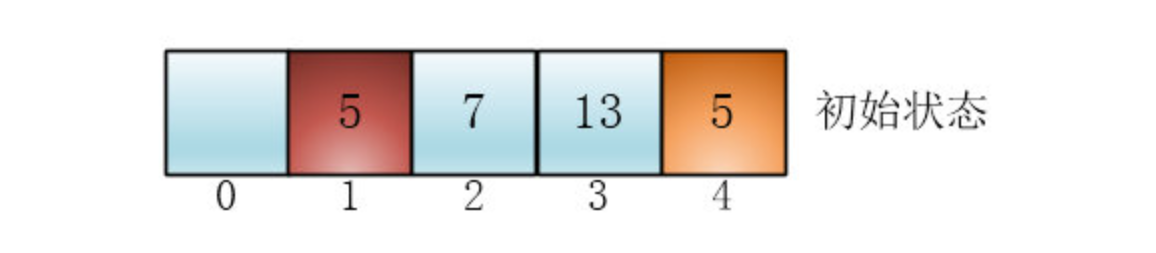
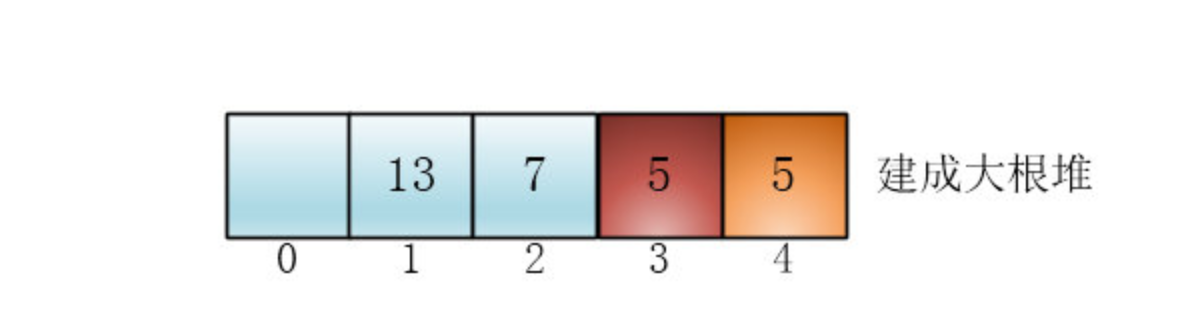
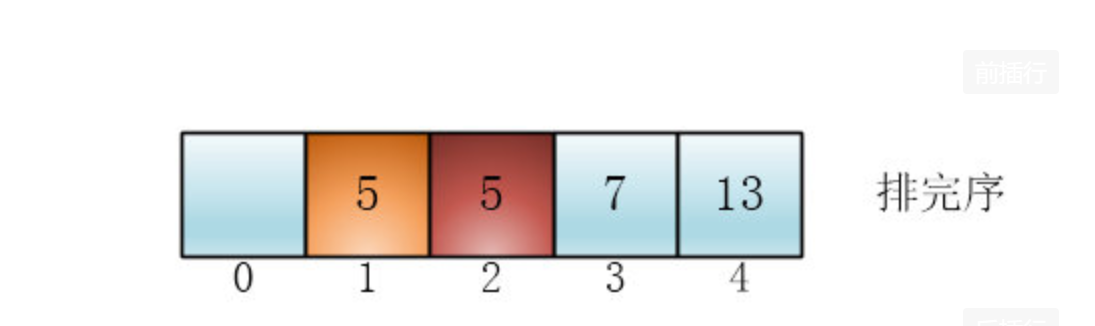
初始状态的5的先后顺序和排完序的顺序明显不一样了(黄色5跑到红色5左边去了),所以这个排序不是稳定的

