N皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
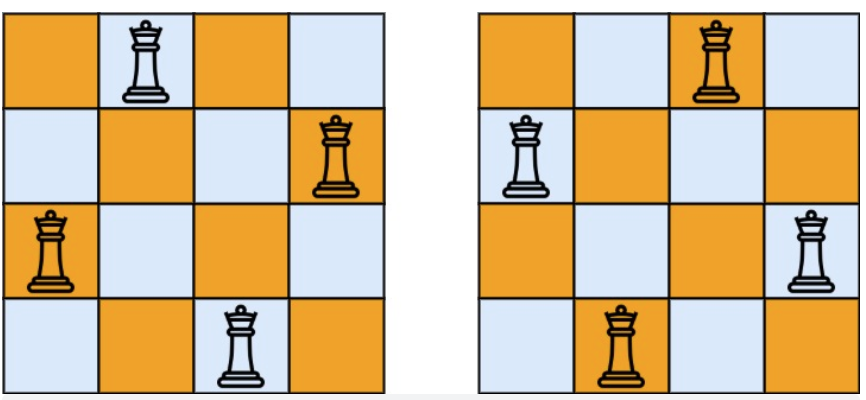
- 输入:n = 4
- 输出:[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
- 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
- 输入:n = 1
- 输出:[["Q"]]
思路
如何使用回溯方法去搜索一个二维数组?(难点)
其实本题的难点就主要是对于二维数组的操作的不熟练造成的,画个图示先再说:

上图展示了在一个 4X4 的棋盘中,其中一种正确摆放结果的获取过程。如图所示,实际上在棋盘(二维数组)中搜索摆放结果时,可以逐层搜索
即:把每层递归看做棋盘中的一层,当前递归处理当前层棋盘的搜索任务
那么棋盘有多大,最后就会触发多少层递归(这里是 4X4 所以有4层递归)
二维矩阵中矩阵的高就是这棵树的高度,矩阵的宽就是树形结构中每一个节点的宽度。当我们遍历到棋盘的最底层时也就到了叶子节点处,此时搜索结束。(结束条件)
代码分析
还是老一套,回溯三部曲
三部曲
1、确定回溯函数的参数以及返回值
看题目给的输出结果得知,我们仍需定义一个二维结果数组res;
输入参数有:棋盘的大小n, 遍历行数记录遍历row以及一维数组chessboard(充当单层棋盘,不要在一开头就定义,因为要每行都清空)
class Solution {
private:
vector<vector<string>> res;
void backtracking(int n, int row, vector<string>& chessboard){//确定回溯函数的参数以及返回值
}
public:
vector<vector<string>> solveNQueens(int n) {
}
};
2、确定终止条件
根据上面的讨论,我们希望在遍历到棋盘底部的时候结束
这很好判断,通过row来看即可,row == n就到底了
class Solution {
private:
vector<vector<string>> res;
void backtracking(int n, int row, vector<string>& chessboard){//确定回溯函数的参数以及返回值
//确定终止条件
if(row == n){//将单层棋盘结果,也就是chessboard,保存至二维结果数组
res.push_back(chessboard);
return;
}
}
public:
vector<vector<string>> solveNQueens(int n) {
}
};
3、确定单层处理逻辑
变量row代表着棋盘的行,也控制着递归的深度
而每层里面的for中的循环变量我们命名为col,其控制着棋盘的列
通过行列变量的配合最终确定皇后的位置
与此同时,在单层处理逻辑中,我们还要加入对N皇后问题规则进行判断的函数isVaild,用以确定当前摆放位置是否合法
class Solution {
private:
vector<vector<string>> res;
void backtracking(int n, int row, vector<string>& chessboard){//确定回溯函数的参数以及返回值
//确定终止条件
if(row == n){//将单层棋盘结果,也就是chessboard,保存至二维结果数组
res.push_back(chessboard);
return;
}
//确定单层处理逻辑,每次都从新的列开始搜,因此col初始值是0
for(int col = 0; col < n; ++col){
if(isVaild()){
chessboard[row][col] = 'Q';
backtracking(n, row + 1, chessboard);
chessboard[row][col] = '.';//题干中给了用'.'表示空
}
}
}
public:
vector<vector<string>> solveNQueens(int n) {
}
};
注意在进入下一层递归时要跳过当前行
规则判断函数isVaild
在N皇后问题中,皇后的摆放规则如下:
- 同一行上不能有两个皇后(不能同行)
- 同一列上不能有两个皇后(不能同列)
- 45度和135度角斜线上不能有两个皇后(不能同斜线)
那么我们只要在isVaild函数中对行、列以及斜线上的皇后情况进行检查就行
那么容易得出,isVaild函数的输入参数是与回溯函数相同的,即int n, int row, vector<string>& chessboard
不过,我们还需要将col也作为参数输入,既然要检查行,行不能不给啊
bool isVaild(int row, int col, vector<string>& chessboard, int n){
//检查列,就要指定列遍历行
for(int i = 0; i < row, ++i){
if(chessboard[i][col] == 'Q') return false;
}
//检查45°,以4X4为例,检查以下坐标
//(0,0)(1,1)(2,2)(3,3)
for(int i = row - 1, j = col - 1; i >= 0 && j>= 0; --i , --j){
if(chessboard[i][j] == 'Q') return false;
}
//检查135°
//检查除45°涉及的坐标以外的所有坐标,顺序可能是乱的,但一定都会检查到,不理解子集画一画想一想
for(int i = row - 1, j = col + 1; i >= 0 && j < n; --i , ++j){//注意条件,j要++
if(chessboard[i][j] == 'Q') return false;
}
return true;
}
注意事项:
1、这里其实我们不用去检查行(类似检查列的那种操作),因为一层递归for只拿行中的一个数,不会有重
2、关于遍历45度和135度的逻辑,如果实在忘了就自己画个图理解一下
3、实现45度和135度遍历时,我们使用的for的遍历条件是关键,请注意记忆
- 45度时,row和col作为输入肯定越给越大,因此i、j的值每次遍历时都会变大,而遍历条件是
i >= 0 && j>= 0,因此需要-- - 135度时,row和col作为输入也会越给越大,但j的遍历条件是要小于n,因此其要++
(有新理解再补充)
完整代码
class Solution {
private:
vector<vector<string>> res;
void backtracking(int n, int row, vector<string>& chessboard){//确定回溯函数的参数以及返回值
//确定终止条件
if(row == n){//将单层棋盘结果,也就是chessboard,保存至二维结果数组
res.push_back(chessboard);
return;
}
//确定单层处理逻辑,每次都从新的列开始搜,因此col初始值是0
for(int col = 0; col < n; ++col){
if(isVaild(row, col, chessboard, n)){
chessboard[row][col] = 'Q';
backtracking(n, row + 1, chessboard);//注意要跳过当前行
chessboard[row][col] = '.';//题干中给了用'.'表示空
}
}
}
bool isVaild(int row, int col, vector<string>& chessboard, int n){
//检查列,就要指定列遍历行
for(int i = 0; i < row, ++i){
if(chessboard[i][col] == 'Q') return false;
}
//检查45°,以4X4为例,检查以下坐标
//(0,0)(1,1)(2,2)(3,3)
for(int i = row - 1, j = col - 1; i >= 0 && j>= 0; --i , --j){
if(chessboard[i][j] == 'Q') return false;
}
//检查135°
//检查除45°涉及的坐标以外的所有坐标,顺序可能是乱的,但一定都会检查到,不理解子集画一画想一想
for(int i = row - 1, j = col + 1; i >= 0 && j < n; --i , ++j){//注意条件,j要++
if(chessboard[i][j] == 'Q') return false;
}
return true;
}
public:
vector<vector<string>> solveNQueens(int n) {
//定义单行棋盘chessboard
vector<string> chessboard(n, '.');
backtracking(n, 0, chessboard);
return res;
}
};