前言

前缀和其实不能说是一种算法，它也并不会单独出现题目中。应该说是一个比较简单，但是容易被人忽略的工具

正文

所谓前缀和，就是一个用来计算数组某个区间内所有数之和的一个工具

以一维来举例

假如我们有一个一维数组a，数组中从1到n存着一共n个数据（第0位不存数据，这个我们后面再解释）。

那么我们就创造一个一维数组b，b的第x位置的数据代表a数组从第1位到第x位所有数之和

那么如果我们需要知道数组第m位到第n位之间所有数的和，我们就可以通过b[n] - b[m-1]来得到答案。

• 如果我们需要知道第1位到第m位所有数之和（闭区间），那么如果我们不想对这种情况使用if进行特殊判断，就要根据之前的式子进行b[m] - b[0]的计算。显然，我们需要b[0] == 0
• 按照我们的对应关系，一维数组b，b的第x位置的数据代表a数组从第1位到第x位所有数之和。那么如果我们的a数组是从第0位开始存数据的，那么我们就不能让b[0] == 0了。所以我们让a从第1位开始其实是为了b[0]的存在服务的
• 注意，其实可以在输入的时候就进行前缀和的运算，这样我们就不用开两个数组了，这个看个人习惯与试题实际情况

一维前缀和

这个属于一个小工具，所以代码十分简单，也基本不需要背代码，知道这个思想自己写也不难

#include<iostream>

using namespace std;

const int N=1e6;
int a[N],b[N];
int n,m;

int main(){
    cin >> n >> m;
    // 输入数据
    for(int i=1;i<=n;i++) cin>>a[i];
    // 前缀和数组初始化
    for(int i=1;i<=n;i++) b[i] = b[i-1] + a[i];
    int l,r;
    while(m--){
        cin>>l>>r;
        // 计算区间中所有数之和
        cout<<b[r] - b[l-1]<<endl;
    }
    return 0;
}

二维前缀和

这个可能会稍微难一点，因为要借助图形来方便理解。

我们的目的是对于一个二维数组，先生成一个b数组，他(x , y)代表这个点与原点区域内的所有值之和，也就是图中区域所有数之和（我们这次写的代码包含边界）

b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + a[i][j];

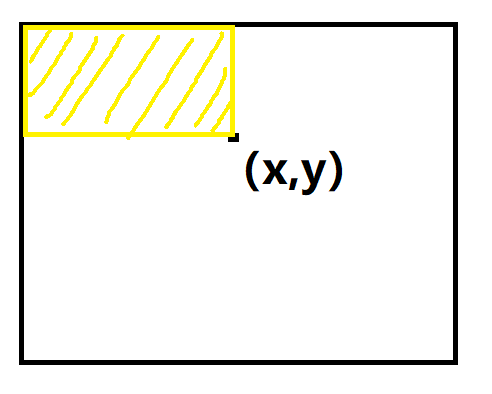
那么我们对程序输入两个坐标，我们就可以通过b数组算出来以这两个点为对角点的矩形内所有数的和

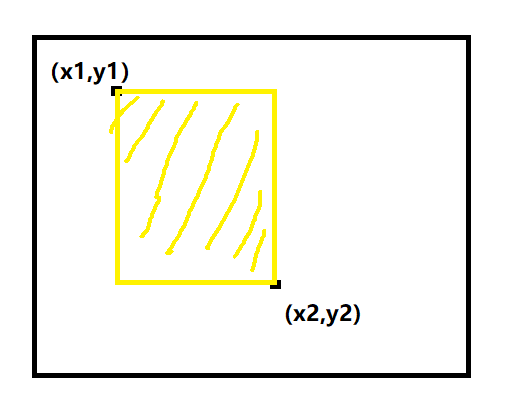
计算方法也很简单，通过图形就会很直观

其实就是b[x2 , y2] - b[x2 , y1-1] - b[x1-1 , y2] + b[x1 , y1]

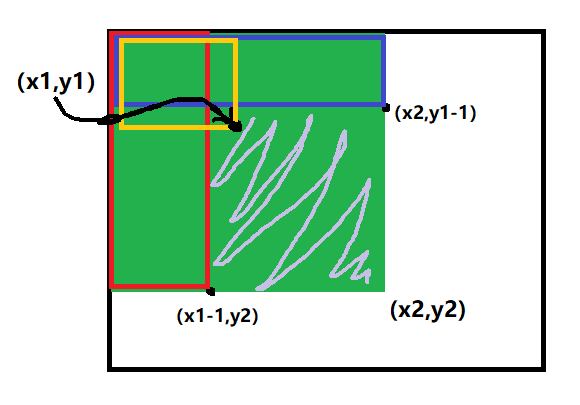
注意，如果但从图像上可能会认为是b[x2 , y2] - b[x2 , y1] - b[x1 , y2] + b[x1 , y1]，但是其实这本质上是数组，不是连续的，所以如果这样写，计算的和是不包括一部分边界值

思路讲完了，上代码

#include<iostream>

using namespace std;

const int N=1010;
int a[N][N],b[N][N];

int main(){
    int n,m,q;
    cin>>n>>m>>q;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            b[i][j] = b[i-1][j] + b[i][j-1] - b[i-1][j-1] + a[i][j];
        }
    }
    int x1,y1,x2,y2;
    while(q--){
        cin>>x1>>y1>>x2>>y2;
        cout<< b[x2][y2] - b[x1-1][y2] - b[x2][y1-1] + b[x1-1][y1-1] <<endl;
    }
    return 0;
}

结语

难得有一个是我听完思路后可以自己完美写出来的东西。

但是这篇文章画图快画死我了。。。