7. 基础算法(II)
7.1 位运算
题目:求 \(a\times b\bmod p\)。\(1\le a,b,p\le 10^{18}\)。
思路:
方法一:快速乘。
类似 4.4 中快速幂的思想。
设 \(b\) 在二进制表示下有 \(k\) 位,其中第 \(i\;(0\le i<k)\) 位的数是 \(c_i\;(c_i\in\{0,1\})\),那么:
\[b=\sum_{i=0}^{k-1}c_{i}2^{i}\tag{7.1} \]于是有:
\[a\times b=a\times {\sum_{i=0}^{k-1}c_{i}2^{i}}=\sum_{i=0}^{k-1}a{c_i2^i}\tag{7.2} \]又因为 \(a\times 2^i=(a\times 2^{i-1})\times 2\),所以我们可以通过递推来求出每个乘积项。时间复杂度 \(O(n\log b)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
int a, b, p;
int mul(int a, int b, int p) {
int ans = 0;
while (b) {
if (b & 1) ans = (ans + a) % p;
a = a * 2 % p;
b >>= 1;
}
return ans;
}
signed main() {
scanf("%lld%lld%lld", &a, &b, &p);
printf("%lld\n", mul(a, b, p));
return 0;
}
方法二:光速乘。
利用 \(a\times b\bmod p=a\times b-\lfloor a\times b/p \rfloor\times p\),令 \(\lfloor a\times b/p \rfloor=c\),那我们如何计算 \(c\) 呢?如果我们用 long double 直接计算 \(a\times b/p\),其在十进制下的有效数字为 \(18\sim 19\) 位,当 \(a,b<p\) 时,\(c\) 也一定小于 \(p\),即 \(c\) 也在 \(18\) 位内。所以我们可以用 long double 计算出 \(a\times b/p\) 的精确值,再用 unsigned long long 将其强制转换为 \(c\)。
由于 \(a\times b-c\times p= a\times b\bmod p< 10^{18}<2^{64}\),则 \(a\times b-c\times p=(a\times b-c\times p)\bmod 2^{64}\),用 unsigned long long 计算 \(x=a\times b,y=c\times p\),最后用 long long 计算 \((x\bmod p-y\bmod p)\bmod p\) 即可。时间复杂度 \(O(1)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
ll a, b, p;
ll mul(ll a, ll b, ll p) {
a %= p, b %= p;
ull c = (long double)a * b / p;
ull x = a * b, y = c * p;
ll ans = ((ll)x % p - (ll)y % p + p) % p;
return ans;
}
int main() {
scanf("%lld%lld%lld", &a, &b, &p);
printf("%lld\n", mul(a, b, p));
return 0;
}
7.2 递归与递推
题目:有 \(T\) 组数据,每组数据包含一个 \(5\times 5\) 的矩阵 \(a\),在每个位置 \((i,j)\;(1\le i,j\le 5)\) 上都有一个灯,若 \(a_{i,j}=0\) 表示灯是关着的,\(a_{i,j}=1\) 表示灯是开着的。每一次操作可以选取一盏灯,并改变其上下左右的灯(如果存在)和其本身的状态(即关着的变成开着的,开着的变成关着的),问能否通过 \(\le 6\) 次操作使所有的灯都打开。能则输出最小步数,不能则输出 -1。\(1\le t\le 500\)。
思路:
显然,已操作过的灯(除非它是关着的)不需要再操作。所以我们可以先用二进制枚举第一行的操作情况,再从第一行枚举到第四行,若位于 \((i,j)\) 位置上的灯没有开,则将 \((i+1,j)\) 位置上的灯操作一次即可(防止影响到左边的灯)。最后判断第五行上的灯是否都打开了。时间复杂度 \(O(2^5\cdot 5^2 T)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
using namespace std;
const int dx[] = {-1, 0, 1, 0, 0}, dy[] = {0, -1, 0, 1, 0};
int t;
bool a[7][7], tmp[7][7];
void change(int x, int y) {
for (int i = 0; i < 5; ++i) {
int x_ = x+dx[i], y_ = y+dy[i];
if (x_ > 0 && x_ < 6 && y_ > 0 && y_ < 6)
a[x_][y_] ^= 1;
}
}
int main() {
scanf("%d", &t);
while (t -- ) {
for (int i = 1; i <= 5; ++i) {
for (int j = 1; j <= 5; ++j)
scanf("%1d", &a[i][j]);
}
int ans = 7, step = 0;
memcpy(tmp, a, sizeof a);
for (int s = 0; s < 32; ++s) {
step = 0; memcpy(a, tmp, sizeof tmp); // 注意要将原数组复制一遍,防止覆盖
for (int i = 1; i <= 5; ++i) {
if (s >> (i-1) & 1)
step ++, change(1, i);
}
for (int i = 1; i <= 4; ++i) {
for (int j = 1; j <= 5; ++j) {
if (!a[i][j])
step ++, change(i+1, j);
}
}
for (int i = 1; i <= 5; ++i) {
if (!a[5][i]) {
step = 7;
break;
}
}
ans = min(step, ans);
}
printf("%d\n", (ans > 6) ? -1 : ans);
}
return 0;
}
题目:给定两个数 \(a,b\),令 \(s\) 为 \(a^b\) 的所有约数之和,求 \(s\bmod 9901\)。\(0\le a,b\le 5\times 10^7\) 且 \(a,b\) 不同时为 \(0\)。
思路:
假设在算数基本定理中,\(a=\prod_{i=1}^m p_i^{r_i}\)(其中 \(p_i\) 为质数,\(r_i\in\mathbb{N}_+\)),则 \(a^b=\prod_{i=1}^m p_i^{r_ib}\)。那么有:
\[s=\prod_{i=1}^m\sum_{j=0}^{r_ib}p_i^j\tag{7.3} \]考虑如何快速计算后面的和式。不妨设 \(sum(p,k)=\sum_{i=0}^{k-1}p^i\),运用分治的思想,当 \(k\) 为偶数时,我们有:
\[\begin{aligned} sum(p,k)&=(1+p+p^2+\cdots+p^{k/2-1})+p^{k/2}(1+p+p^2+\cdots+p^{k/2-1})\\ &=sum(p,k/2)+p^{k/2}sum(p,k/2-1)\\ &=sum(p,k/2)(p^{k/2}+1) \end{aligned}\tag{7.4} \]当 \(k\) 为奇数时,显然有 \(sum(p,k)=sum(p,k-1)+p^{k-1}\),再代入 \((7.4)\) 计算即可。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <unordered_map>
using namespace std;
typedef long long ll;
const int P = 9901;
int a, b, ans = 1;
unordered_map<int, int> primes;
int pow(int a, int b) {
int ans = 1;
while (b) {
if (b & 1) ans = (ll)ans * a % P;
a = (ll)a * a % P;
b >>= 1;
}
return ans;
}
int sum(int p, int k) {
if (k == 1) return 1;
if (k % 2) return (sum(p, k-1) + pow(p, k-1)) % P;
return sum(p, k/2)*(pow(p, k/2)+1) % P;
}
int main() {
scanf("%d%d", &a, &b);
if (!a) puts("0"), exit(0);
for (int i = 2; i <= a/i; ++i) {
while (a % i == 0) {
a /= i;
primes[i] ++;
}
}
if (a > 1) primes[a] ++;
for (auto p : primes) ans = ans * sum(p.first, p.second*b+1) % P;
printf("%d\n", ans);
return 0;
}
例题:AcWing 98. 分形之城
题目:为了更好地规划城市建设,一座城市的工作人员想出了如下图所示的一种方法:
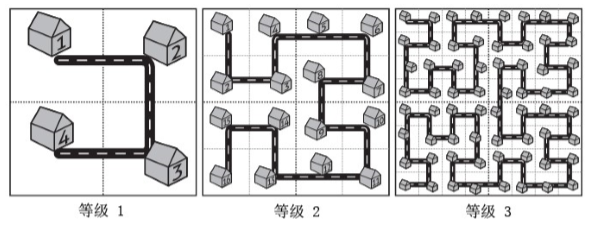
现在,他们想求出编号为 \(A,B\) 的房屋在 \(N\) 级城市的距离,每个小方格的边长都为 \(10\text{m}\),结果四舍五入到整数。多测,有 \(n\) 组数据。
\(1\le N\le 31,1\le A,B\le 2^{2N},1\le n\le 10\)。
思路:
定义 \(pos(A,N)\) 表示编号为 \(A\) 的房屋在 \(N\) 级城市中的位置。由图 \(\texttt{7-1}\) 可知,等级为 \(N\) 的城市是由 \(4\) 个等级为 \(N-1\) 的城市组成,其中左上角的城市顺时针旋转了 \(90^{\circ}\) 再水平翻转,右上角的城市没有旋转,右下角的城市没有旋转,左下角的城市逆时针旋转了 \(90^{\circ}\) 再水平翻转。
在计算 \(pos(A,N)\) 时,由于 \(N-1\) 级城市有 \(2^{2N-2}\) 座房屋,所以我们先递归求解出 \(pos((A-1)\bmod 2^{2N-2}+1,N-1)\),递归出口为 \(pos(1,0)=(1,1)\)。假设求得的解为 \((x,y)\),再根据 \(A/2^{2N-2}\) 的大小即可判断出 \(A\) 属于哪一个部分:
-
若 \(A\) 在左上角:则 \(A\) 顺时针旋转 \(90^{\circ}\) 后为 \((y,2^{N-1}-x+1)\),再水平翻转后为 \((y,x)\);
-
若 \(A\) 在右上角:则 \(A\) 的 \(y\) 坐标增加了 \(2^{N-1}\),坐标变为 \((x,y+2^{N-1})\);
-
若 \(A\) 在右下角:则 \(A\) 的 \(x\) 坐标增加了 \(2^{N-1}\),\(y\) 坐标也增加了 \(2^{N-1}\),坐标变为 \((x+2^{N-1},y+2^{N-1})\);
-
若 \(A\) 在左下角:则 \(A\) 逆时针旋转 \(90^{\circ}\) 后为 \((2^{N-1}-y+1,x)\),再水平翻转后为 \((2^{N-1}-y+1,2^{N-1}-x+1)\),又因为 \(A\) 的 \(x\) 坐标增加了 \(2^{N-1}\),所以坐标变为 \((2^N-y+1,2^{N-1}-x+1)\)。
最后用两点之间距离公式计算出 \(pos(A,N)\) 和 \(pos(B,N)\) 之间的距离即可。
*代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
#define int long long
typedef pair<int, int> pii;
int t, n, a, b;
pii pos(int a, int n) {
if (!n) return make_pair(1, 1);
int t = pow(2, n*2-2);
pii a_ = pos((a-1)%t+1, n-1);
int part = (a-1)/t, x = a_.first, y = a_.second;
if (part == 0) return make_pair(y, x);
else if (part == 1) return make_pair(x, y+(int)pow(2, n-1));
else if (part == 2) return make_pair(x+(int)pow(2, n-1), y+(int)pow(2, n-1));
else return make_pair((int)pow(2, n)-y+1, (int)pow(2, n-1)-x+1);
}
int dist(pii a, pii b) {
return round(sqrt(pow(a.first*10-b.first*10, 2)+pow(a.second*10-b.second*10, 2)));
}
signed main() {
scanf("%lld", &t);
while (t -- ) {
scanf("%lld%lld%lld", &n, &a, &b);
printf("%lld\n", dist(pos(a, n), pos(b, n)));
}
return 0;
}
7.3 前缀和与差分
题目:地图上有 \(n\) 个目标,第 \(i\) 个目标位于 \((x_i,y_i)\),价值为 \(w_i\)(多个目标可能在同一位置)。现有一束激光炸弹,覆盖面积为一个 \(m\times m\) 的正方形,但正方形边上的点不会被轰炸,且正方形的边必须与 \(x\) 轴或 \(y\) 轴平行。求能轰炸的最大价值。\(0\le m\le 10^9,0<n\le 10000,0\le x_i,y_i\le 5000,0\le w_i\le 1000\)。
思路:
由于 \(0\le x_i,y_i\le 5000\),我们可以用二维前缀和完成此题。令 \(a_{i,j}\) 表示位置 \((i,j)\) 上的目标的价值之和,\(s_{i,j}=s_{i,j-1}+s_{i-1,j}-s_{i-1,j-1}+a_{i,j}\)。注意到在二维前缀和中,我们将 \((x_i,y_i)\) 作为一个格子来处理,而题目中的 \((x_i,y_i)\) 为格点,且正方形边上的点不会被轰炸。我们可以认为正方形左上角的点为 \((x_i-0.5,y_i-0.5)\),正方形右下角的点为 \((x_i+0.5, y_i+0.5)\),这个问题与原问题是等价的。
最后我们枚举正方形的右下角 \((i,j)\) 即可。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 5005;
int n, m, ans;
int s[N][N];
int main() {
scanf("%d%d", &n, &m);
m = min(m, 5001);
for (int i = 1; i <= n; ++i) {
int x, y, w; scanf("%d%d%d", &x, &y, &w);
x ++, y ++;
s[x][y] += w;
}
for (int i = 1; i <= 5001; ++i) {
for (int j = 1; j <= 5001; ++j)
s[i][j] += s[i-1][j] + s[i][j-1] - s[i-1][j-1];
}
for (int i = m; i <= 5001; ++i) {
for (int j = m; j <= 5001; ++j)
ans = max(ans, s[i][j]-s[i-m][j]-s[i][j-m]+s[i-m][j-m]);
}
printf("%d\n", ans);
return 0;
}
题目:有一个长度为 \(n\) 的序列 \(a\),每次可以选择一个区间 \([l,r]\), \(a_l\sim a_r\) 都加 \(1\) 或减 \(1\)。求至少需要几次操作才能使数列中的数全部相同,并计算在操作次数最少的情况下,最终得到的序列可能有多少种。\(1\le n\le 10^5,0\le a_i<2^{31}\)。
思路:
我们求出 \(a\) 的差分序列 \(b\),令 \(b_{n+1}=0\)。显然对于题目的一次操作,相当于 \(b_l\) 增加(或减少)\(1\),\(b_{r+1}\) 减少(或增加)\(1\)。我们的目标是将 \(b_2,b_3,\cdots,b_n\) 全部变为 \(0\)。那么最终得到的序列 \(a\) 就是由 \(n\) 个 \(b_1\) 组成的。我们可以分类讨论 \(l,r\) 的取值:
- \(2\le l\le r<n\):这样可以改变 \(b_l,b_{r+1}\) 两个值。我们应在保证 \(b_l,b_{r+1}\) 一正一负时,尽量多地采取这种操作。
- \(l=1,2\le r<n\):这样可以将 \(b_{r+1}\) 减少 \(1\)。
- \(2\le l\le n,r=n\):这样可以将 \(b_l\) 增加 \(1\)。
- \(l=1,r=n\):这样对 \(b_2,b_3,\cdots,b_n\) 没有影响,相当于浪费了一次操作。
设 \(b_2,b_3,\cdots,b_n\) 中正数之和为 \(p\),负数之和的绝对值为 \(q\)。则第一种操作最多可以进行 \(\min(p,q)\) 次,剩下的数的绝对值为 \(|p-q|\),每个数可以执行第二种操作或第三种操作,需要进行 \(|p-q|\) 次。这样,最少操作次数就为 \(\min(p,q)+|p-q|=\max(p,q)\),\(a\) 就有 \(|p-q|+1\) 种可能。
*代码
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
int n; ll p, q;
int a[N], b[N];
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &a[i]);
b[i] = a[i] - a[i-1];
}
for (int i = 2; i <= n; ++i) {
if (b[i] > 0) p += (ll)b[i];
else q += (ll)-b[i];
}
printf("%lld\n%lld\n", max(p, q), abs(p-q)+1);
return 0;
}
7.4 二分
题目:给定一个长度为 \(n\) 的正整数数列 \(a\),求一个平均数最大的、长度不小于 \(L\) 的连续子段。求出平均数最大值乘 \(1000\) 后向下取整的值。\(1\le L\le n\le 10^5,1\le a_i\le 2000\)。
思路:
这道题并没有明显的二分的特征。我们可以考虑二分答案,若最优解为 \(x\),则当 \(mid\le x\) 时,必然可以找到一段,使得其平均值大于等于 \(mid\);否则一定找不到。即答案满足单调性。
如果我们将子段中的每个数都减去二分的值,就转化为判断“是否存在一个长度不小于 \(L\) 的子段,字段和非负”。我们考虑以下两个子问题:
-
求一个子段,它的和最大:我们可以 \(O(n)\) 扫描原数列,初始时 \(sum=0\),每次 \(sum\) 增加 \(a_i\),若 \(sum<0\),则令 \(sum=0\)。该过程中 \(sum\) 的最大值即为所求。
-
求一个子段,它的和最大,子段的长度不小于 \(L\):子段和可以转化为前缀和相减的形式。令 \(s_i=\sum_{j=1}^i a_j\),则所求即为:
\[\max_{i-j\ge L}\{a_{j+1}+a_{j+2}+\cdots+a_i\}=\max_{L\le i\le n}\{s_i-\min_{0\le j\le i-L}\{s_j\}\}\tag{7.5} \]注意到,随着 \(i\) 的增长,\(j\) 的取值范围每次只会增加 \(1\)。所以我们可以用一个变量记录当前最小值,每次与新的取值取最小值即可。
解决了问题 2 之后,我们只需要判断最大字段和是不是非负数,就可以确定二分上下界了。
时间复杂度 \(O(n\log n)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e5+10;
const double eps = 1e-5;
int n, L;
double a[N], b[N], s[N];
int main() {
scanf("%d%d", &n, &L);
for (int i = 1; i <= n; ++i) scanf("%lf", &a[i]);
double l = -1e6, r = 1e6;
while (r - l > eps) {
double mid = (l + r) / 2;
for (int i = 1; i <= n; ++i) b[i] = a[i] - mid;
for (int i = 1; i <= n; ++i) s[i] = s[i-1] + b[i];
double ans = -1e10, minl = 1e10;
for (int i = L; i <= n; ++i) {
minl = min(minl, s[i-L]);
ans = max(ans, s[i]-minl);
}
if (ans >= 0) l = mid;
else r = mid;
}
printf("%d\n", (int)(r*1000));
return 0;
}
题目:有 \(n\) 个元素,每对元素之间的大小关系是确定的且没有相同的元素,关系不具有传递性,也就是说,元素之间的大小关系是 \(n\) 个点与 \(\dfrac{n(n-1)}{2}\) 条有向边构成的任意有向图。你需要通过不超过 \(10000\) 次询问来确定这些元素的大小关系,每次询问你需要调用 compare 函数并传入两个参数 \(i,j\;(1\le i,j\le n)\),若编号为 \(i\) 的元素小于编号为 \(j\) 的元素则 compare 函数返回 true,否则返回 false。\(1\le n\le 1000\)。
思路:假设前 \(k-1\) 个元素已经排好,我们就可以通过二分找到第 \(k\) 个元素的位置。那么将 \(n\) 个元素全部排好的询问次数不超过 \(n\log n\)。
代码:
// Forward declaration of compare API.
// bool compare(int a, int b);
// return bool means whether a is less than b.
class Solution {
public:
vector<int> specialSort(int N) {
vector<int> ans;
ans.push_back(1);
for (int i = 2; i <= N; ++i) {
int l = 0, r = ans.size()-1;
while (l <= r) {
int mid = l + r>> 1;
if (compare(ans[mid], i)) l = mid + 1;
else r = mid - 1;
}
ans.insert(ans.begin()+l, i);
}
return ans;
}
};
7.5 排序
题目:有一个 \(n\times m\) 的矩阵,其中有 \(t\) 个位置 \((x_i,y_i)\) 的值为 \(1\),其余位置的值为 \(0\)。你可以进行任意多次操作,每次可以将相邻两个位置的值交换,注意第一行与最后一行,第一列与最后一列也视作相邻。问最后能否使每一行、每一列的价值之和分别相等,如果可以,输出最小操作次数。\(1\le n,m\le 10^5,0\le t\le \min(nm,10^5)\)。
思路:
显然,交换相邻两列的值对所有行都不会产生影响,交换相邻两行的值对所有列也不会产生影响。所以我们可以将行和列分开计算。这样,原问题就可以转换为环形均分纸牌问题:有 \(n\) 个人围成一圈,第 \(i\) 个人初始时有 \(a_i\) 颗糖果,每次一个人可以给相邻的人一颗糖果,问最少需要几次操作才能使所有人的糖果数都相等。显然 \(n\) 不能整除糖果总数时无解,接下来我们来讨论有解的情况。
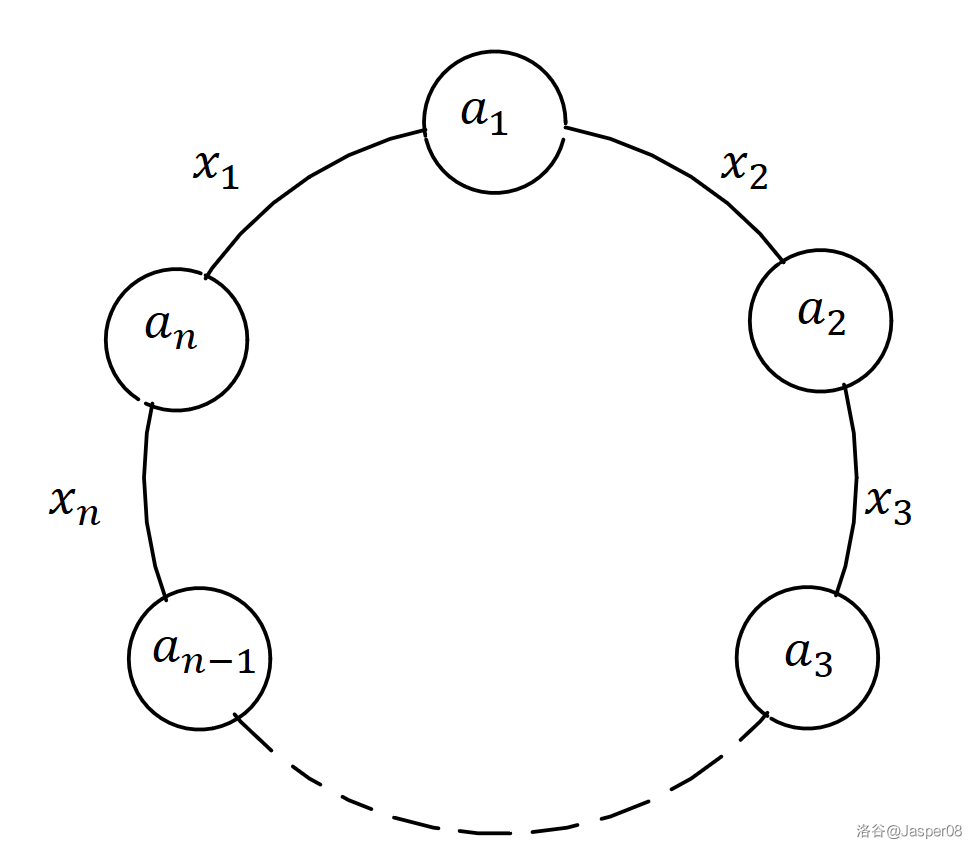
如图 \(\texttt{7-2}\),假设第 \(n\) 个人给第 \(1\) 个人 \(x_1\) 颗糖果,第 \(1\) 个人给第 \(2\) 个人 \(x_2\) 颗糖果,……,第 \((n-1)\) 个人给第 \(n\) 个人 \(x_n\) 颗糖果,那么有:
\[\left\{\begin{aligned} &a_1+x_1-x_2=\bar a\\ &a_2+x_2-x_3=\bar a\\ &\cdots\\ &a_n+x_n-x_1=\bar a \end{aligned}\right.\tag{7.6} \]其中,\(\bar a=\dfrac{1}{n}\sum_{i=1}^n a_i\)。将所有 \(x_i\) 都用 \(x_1\) 表示出来,就有:
\[\left\{\begin{aligned} &x_1=x_1\\ &x_2=a_1-\bar a+x_1\\ &x_3=a_1+a_2-2\bar a+x_1\\ &\cdots \\ &x_n=a_1+a_2+\cdots +a_{n-1}-(n-1)\bar a+x_1 \end{aligned}\right.\tag{7.7} \]设 \(c_i=\sum_{k=1}^{i-1}a_i-(i-1)\bar a\),特别地,令 \(c_1=0\)。则 \((7.7)\) 可化为:
\[\left\{\begin{aligned} &x_1=x_1-c_1\\ &x_2=x_1-c_2\\ &x_3=x_1-x_3\\ &\cdots \\ &x_n=x_1-c_n \end{aligned}\right.\tag{7.8} \]那么所求的最小值即为 \(|x_1|+|x_2|+\cdots+|x_n|=|x_1-c_1|+|x_1-c_2|+\cdots+|x_1-c_n|\),根据绝对值不等式,可知将 \(c\) 数组从小到大排序后,该式在 \(x_1=c_{\lceil(n+1)/2\rceil}\) 时取得最小值。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
#define int long long
const int N = 1e5+10;
int n, m, t;
int row[N], col[N];
int c[N];
int check(int n, int a[]) {
if (t % n) return -1;
memset(c, 0, sizeof c);
int avr = t / n, sum = 0;
for (int i = 1; i <= n; ++i) c[i] = sum - (i-1) * avr, sum += a[i];
sort(c+1, c+n+1);
int ans = 0;
for (int i = 1; i <= n; ++i) ans += abs(c[i]-c[(n+1)/2]);
return ans;
}
signed main() {
scanf("%lld%lld%lld", &n, &m, &t);
for (int i = 1; i <= t; ++i) {
int x, y; scanf("%lld%lld", &x, &y);
row[x] ++, col[y] ++;
}
int ansr = check(n, row), ansc = check(m, col);
if (ansr != -1 && ansc != -1) printf("both %lld\n", ansr+ansc);
else if (ansr != -1) printf("row %lld\n", ansr);
else if (ansc != -1) printf("column %lld\n", ansc);
else puts("impossible");
return 0;
}
题目:给定 \(P\) 组数据,每组数据包含 \(m\) 个整数 \(a\),每当输入的整数个数为奇数时,输出当前输入的所有数的中位数。\(1\le P\le 1000,1\le m\le 99999\),且 \(\sum m\le 5\times 10^5\)。
思路:
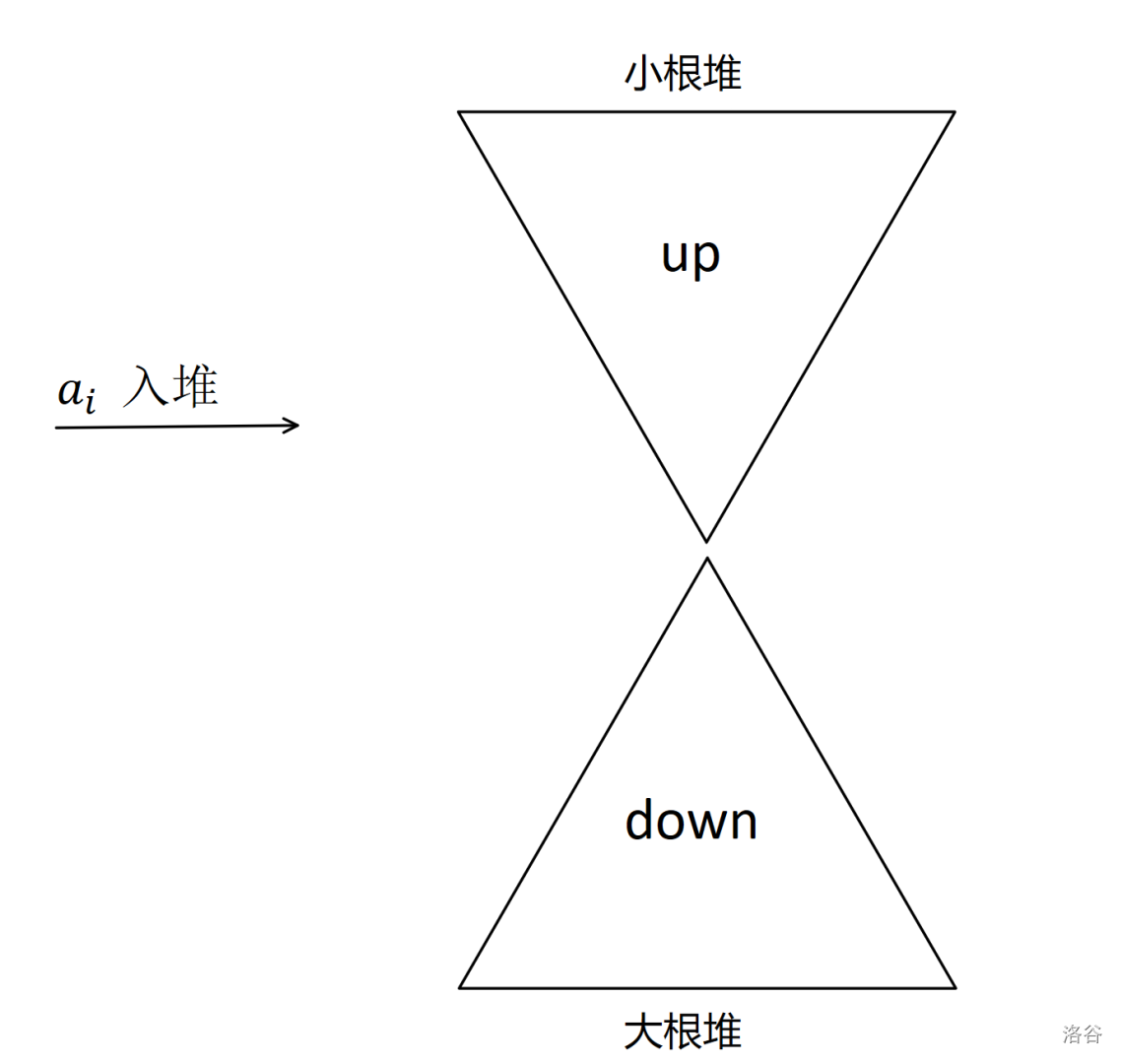
如图 \(\texttt{7-3}\),我们可以维护一个小根堆 \(\texttt{up}\) 和一个大根堆 \(\texttt{down}\),其中 \(\texttt{down}\) 存储较小的部分,\(\texttt{up}\) 存储较大的部分。保证 \(\texttt{down.size()}=\texttt{up.size()}\) 或 \(\texttt{down.size()}=\texttt{up.size()}+1\)。中位数即为 \(\texttt{down.top()}\)。每次 \(a_i\) 入堆时,我们考虑 \(a_i\) 应该放在哪个堆中:
- 若 \(a_i\ge\texttt{down.top()}\):说明 \(a_i\) 大于等于当前中位数,要插入到 \(\texttt{up}\) 中;
- 若 \(a_i<\texttt{down.top()}\):说明 \(a_i\) 小于当前中位数,要插入到 \(\texttt{down}\) 中。
我们还需要维护两个堆的大小关系。若 \(\texttt{down.size()}>\texttt{up.size()}+1\),则将 \(\texttt{down.top()}\)(即 \(\texttt{down}\) 中最大的数)插入到 \(\texttt{up}\) 中;若 \(\texttt{up.size()}>\texttt{down.size()}\),则将 \(\texttt{up.top()}\)(即 \(\texttt{up}\) 中最小的数)插入到 \(\texttt{down}\) 中。
时间复杂度 \(O(Tm\log m)\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <vector>
using namespace std;
int p, s, m;
int main() {
scanf("%d", &p);
while (p -- ) {
scanf("%d%d", &s, &m);
printf("%d %d\n", s, (m+1)/2);
int cnt = 0;
priority_queue<int, vector<int>, less<int>> down;
priority_queue<int, vector<int>, greater<int>> up;
for (int i = 1; i <= m; ++i) {
int x; scanf("%d", &x);
if (down.size() && x >= down.top()) up.push(x);
else down.push(x);
if (down.size() > up.size()+1) up.push(down.top()), down.pop();
if (up.size() > down.size()) down.push(up.top()), up.pop();
if (i & 1) {
printf("%d ", down.top());
cnt ++;
if (cnt % 10 == 0) puts("");
}
}
if (cnt % 10) puts("");
}
return 0;
}
题目:有多组测试数据,每组数据包含 \(n\) 个整数 \(a_i\),每次操作可以选择两个整数 \(1\le i,j\le n\;(i\ne j)\) 并交换 \(a_i,a_j\)。问至少要几次操作才能将 \(a\) 数组升序排列。\(1\le n\le 5\times 10^5,1\le a_i<10^{10}\)。
思路:显然题目所求的即为 \(a\) 中逆序对的数量。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define int long long
const int N = 5e5+10;
int n, a[N], tmp[N];
int merge_sort(int l, int r) {
if (l >= r) return 0;
int mid = l + r >> 1;
int ans = merge_sort(l, mid) + merge_sort(mid+1, r);
int i = l, j = mid+1, k = 1;
while (i <= mid && j <= r) {
if (a[i] <= a[j]) tmp[k ++] = a[i ++];
else tmp[k ++] = a[j ++], ans += mid-i+1;
}
while (i <= mid) tmp[k ++] = a[i ++];
while (j <= r) tmp[k ++] = a[j ++];
for (int i = l, j = 1; i <= r; ++i, ++j) a[i] = tmp[j];
return ans;
}
signed main() {
scanf("%lld", &n);
while (n) {
for (int i = 1; i <= n; ++i) scanf("%lld", &a[i]);
int ans = merge_sort(1, n);
printf("%lld\n", ans);
scanf("%lld", &n);
}
return 0;
}
7.6 RMQ
题目:给定 \(n\) 个整数 \(a_i\) 和 \(m\) 次询问,每次询问给定两个整数 \(l,r\;(1\le l\le r\le n)\),求出 \(\max_{i=l}^r a_i\)。\(1\le n\le 2\times 10^5,1\le m\le 10^4\)。
思路:
我们可以用 ST 表来完成这道题,其运用的是倍增的思想。令 \(f_{i,j}\) 表示以 \(i\) 为区间左端点,区间长度为 \(2^j\) 的区间中的最大值。初始转态为 \(f_{i,0}=a_i\)。考虑如何转移:由于 \(f_{i,j}\;(j>0)\) 表示区间 \([i,i+2^j-1]\) 中的最大值,我们可以将其分为两个区间 \([i,i+2^{j-1}-1]\) 和 \([i+2^{j-1},i+2^{j}-1]\),那么有:
\[f_{i,j}=\max\{f_{i,j-1},f_{i+2^{j-1},j-1}\}\tag{7.9} \]接下来考虑如何处理询问。令 \(k\lfloor\log_2(r-l+1)\rfloor\),显然有 \(ans=\max(f_{l,k},f_{r-2^{k}+1,k})\)。
代码:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;
const int N = 5e5+10, M = 20;
int n, m;
int a[N], f[N][M];
int query(int l, int r) {
int k = log2(r-l+1);
return max(f[l][k], f[r-(1<<k)+1][k]);
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), f[i][0] = a[i];
for (int j = 1; (1<<j) <= n; ++j) {
for (int i = 1; i+(1<<j)-1 <= n; ++i)
f[i][j] = max(f[i][j-1], f[i+(1<<j-1)][j-1]);
}
int l, r;
scanf("%d", &m);
while (m --) {
scanf("%d%d", &l, &r);
printf("%d\n", query(l, r));
}
return 0;
}