代码随想录算法训练营Day24|77. 组合
回溯基础
回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,常见的问题类型为:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
我们在处理时需要区分「组合问题」和「排列问题」,组合是不强调元素顺序的,排列是强调元素顺序。
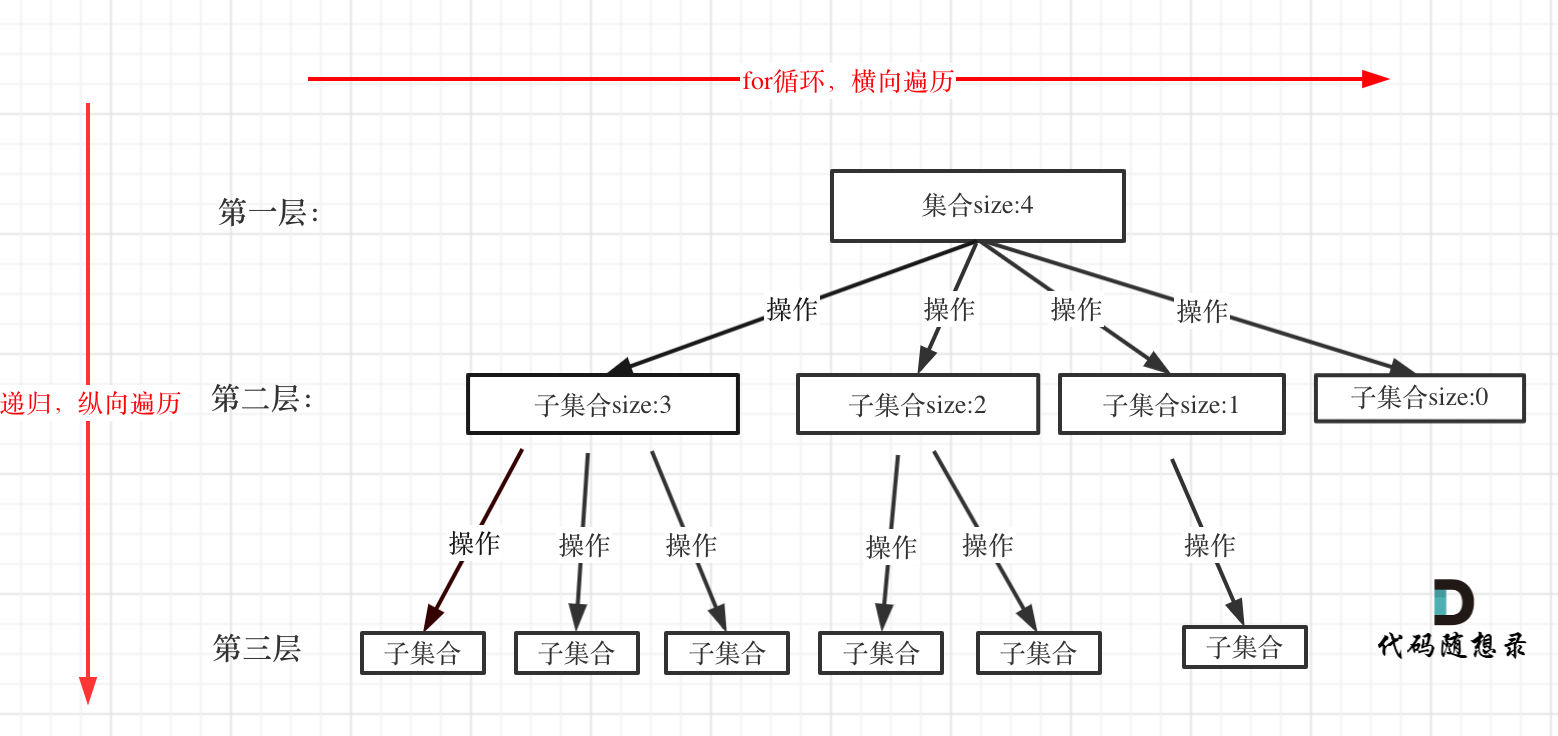
所有回溯法的问题都可以抽象为树形结构!因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度都构成的树的深度。
77. 组合
题目要求1 <= k <= n,在完成函数时不需要进行异常处理。
本题需要遍历所有的可能,并且进行回溯,对应的N叉树的宽度为数的范围n,树的深度为要求的组合个数k。(意味着面临几次选择)对应的N叉树如图所示:
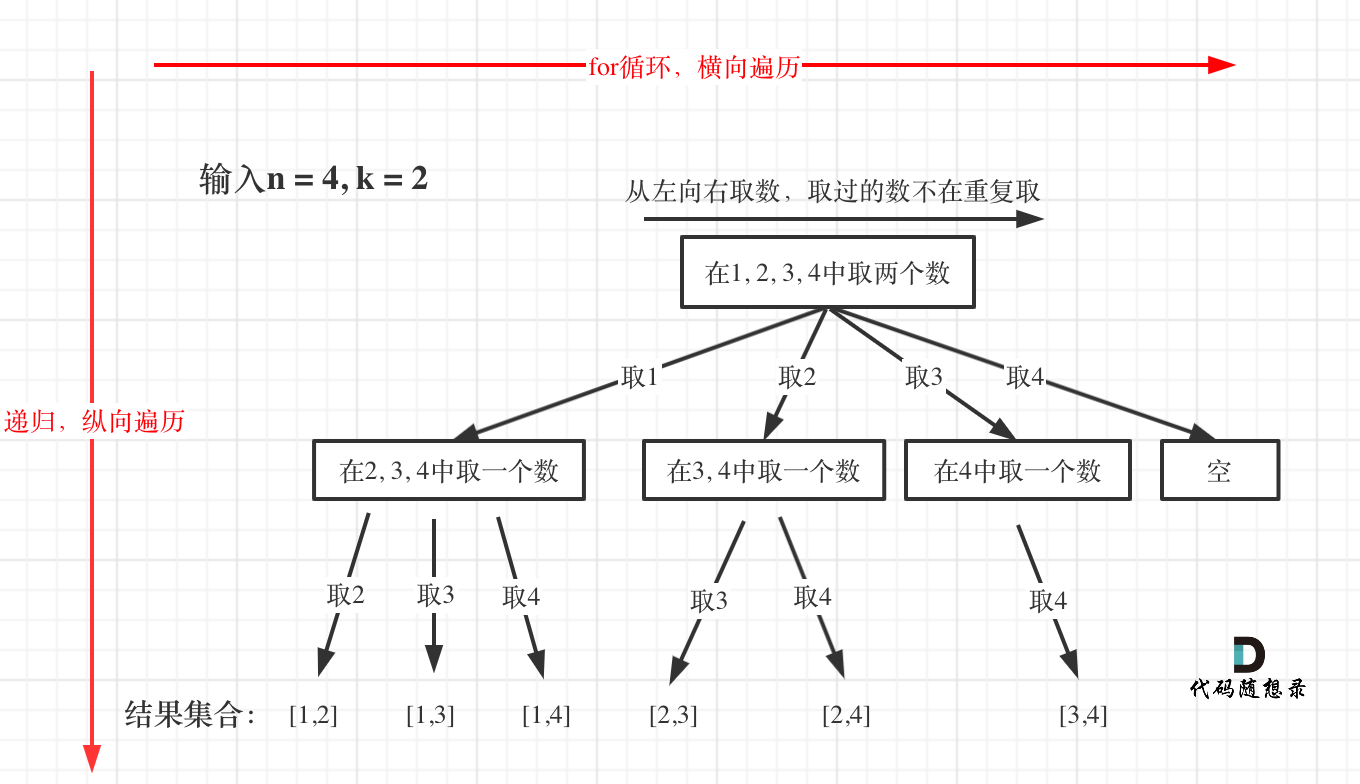
题目要求k个数的组合,表明每个数仅能使用一次。这里我们通过「从左向右」遍历来实现。
for (int i = startIndex; i <= n; i++) {
path.push_back(i);
backtracking(n, k, i + 1);
// 体现回溯思想
path.pop_back();
}
注意每次递归时需要将startIndex向前移位一格。
另外我们可以在进入递归前进行剪枝操作,思路为“如果「剩余需要选择的次数」小于「需要达标的组合个数」”,那么就没有继续递归的必要了:
// 剪枝:如果路径已有长度与startIndex剩余长度小于k,则无法匹配成功
if (path.size() + n - startIndex + 1 < k) return;
完整代码如下:
class Solution {
public:
vector<vector<int>> combine(int n, int k) {
backtracking(n, k, 1);
return res;
}
void backtracking(int n, int k, int startIndex) {
if (path.size() == k) {
res.push_back(path);
return;
}
// 剪枝:如果路径已有长度与startIndex剩余长度小于k,则无法匹配成功
if (path.size() + n - startIndex + 1 < k) return;
for (int i = startIndex; i <= n; i++) {
path.push_back(i);
backtracking(n, k, i + 1);
// 体现回溯思想
path.pop_back();
}
}
private:
vector<vector<int>> res;
vector<int> path;
};
注意遍历过程中传入参数startIndex