首页 > 编程语言 >代码随想录算法训练营Day16| 104. 二叉树的最大深度、559.n叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数

代码随想录算法训练营Day16| 104. 二叉树的最大深度、559.n叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数

时间：2022-12-06 23:57:24浏览次数：90  
标签：node right TreeNode val int 随想录 二叉树 深度 left

代码随想录算法训练营Day16| 104. 二叉树的最大深度、559.n叉树的最大深度、111. 二叉树的最小深度、222. 完全二叉树的节点个数

104. 二叉树的最大深度

104. 二叉树的最大深度

而根节点的高度就是二叉树的最大深度。

①递归法

我们使用「左右中」的后序遍历方式求根节点的高度。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        return searchMaxDepth(root);
    }

    int searchMaxDepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftDepth = searchMaxDepth(node->left);
        int rightDepth = searchMaxDepth(node->right);
        return max(leftDepth, rightDepth) + 1;
    }
};

②迭代法

使用层序遍历是最为合适的，因为最大的深度就是二叉树的层数，和层序遍历的方式极其吻合。

层序遍历

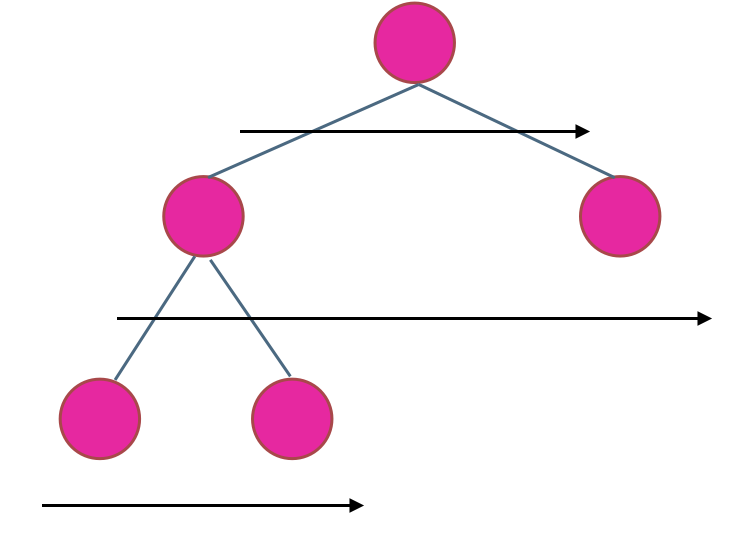
代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> que;
        if (root == NULL) return 0;
        else que.push(root);
        int res = 0;
        while (!que.empty()) {
            int size = que.size();
            res++; // 记录深度
            while (size--) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return res;
    }
};

559.n叉树的最大深度

559. N 叉树的最大深度

将二叉树的情况推广到n叉树，思路类似。

①递归法

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        return searchMaxDepth(root);
    }

    int searchMaxDepth(Node* node) {
        if (node == NULL) return 0;
        int maxDepth = 0;
        for (Node* child : node->children) {
            int tmp = searchMaxDepth(child);
            maxDepth = tmp > maxDepth ? tmp : maxDepth;
        }
        return maxDepth + 1;
    }
};

②迭代法

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    int maxDepth(Node* root) {
        queue<Node*> que;
        if (root == NULL) return 0;
        else que.push(root);
        int res = 0;
        while (!que.empty()) {
            int size = que.size();
            res++;
            while (size--) {
                Node* node = que.front();
                que.pop();
                for (Node* child : node->children) {
                    if (child) que.push(child);
                }
            }
        }
        return res;
    }
};

111. 二叉树的最小深度

111. 二叉树的最小深度

本题有一个误区，在处理节点的过程中，最大深度很容易理解，最小深度就不那么好理解，如图：

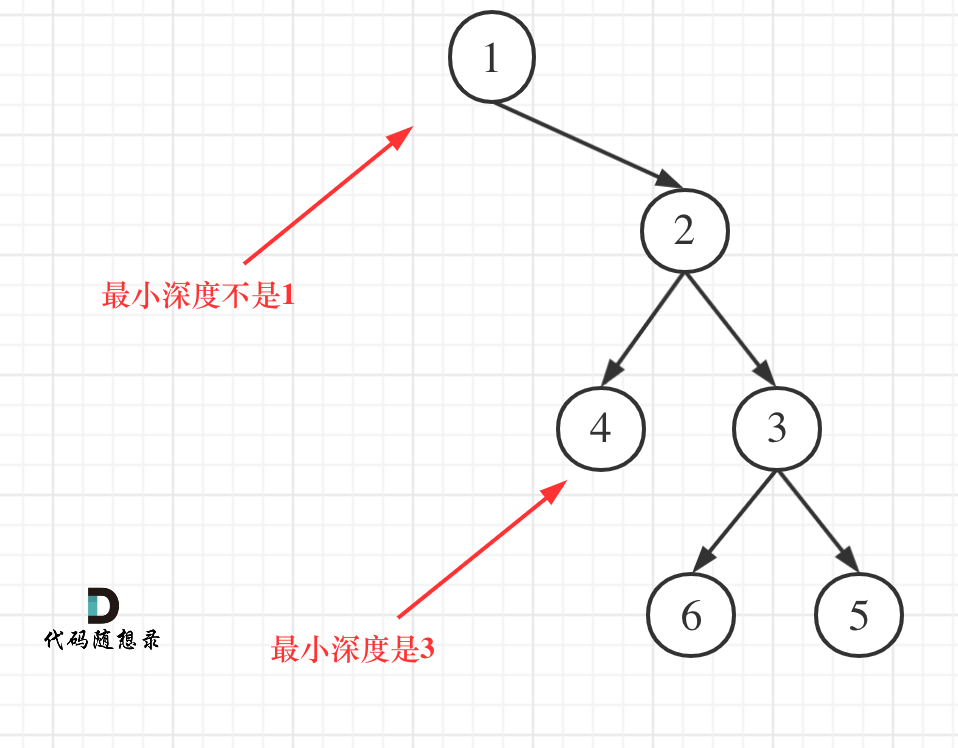
111.二叉树的最小深度

最小深度是从根节点到最近叶子节点的最短路径上的节点数量，注意终点是叶子节点。（左右孩子节点必须为空！）

①递归法

递归首先确定递归的三步骤：

  1. 确定递归函数的参数和返回值

参数为要传入的二叉树根节点，返回的是int类型的深度。代码如下：

int getDepth(TreeNode* node)
  1. 确定终止条件

终止条件也是遇到空节点返回0，表示当前节点的高度为0。代码如下：

if (node == NULL) return 0;
  1. 确定单层递归的逻辑

这块和求最大深度可就不一样了，一些同学可能会写如下代码：

int leftDepth = getDepth(node->left);
int rightDepth = getDepth(node->right);
int result = 1 + min(leftDepth, rightDepth);
return result;

如果这么求的话，没有左孩子的分支会算为最短深度。所以需要对左右孩子是否为空进行讨论：

  • 所以，如果左子树为空，右子树不为空，说明最小深度是 1 + 右子树的深度。

  • 反之，右子树为空，左子树不为空，最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空，返回左右子树深度最小值 + 1 。

完整代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        return getMinDepth(root);
    }

    int getMinDepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftDepth = getMinDepth(node->left);
        int rightDepth = getMinDepth(node->right);
        // 要考虑孩子节点为空的情况
        if (node->left == NULL && node->right != NULL) return rightDepth + 1;
        if (node->left != NULL && node->right == NULL) return leftDepth + 1;
        return min(leftDepth, rightDepth) + 1;
    }
};

②迭代法

层序遍历即可，重点在于判断最小深度的时机：只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        queue<TreeNode*> que;
        if (root == NULL) return 0;
        else que.push(root);
        int res = 0;
        while (!que.empty()) {
            int size = que.size();
            res++;
            while (size--) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left == NULL && node->right == NULL) return res;
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return res;
    }
};

222. 完全二叉树的节点个数

222. 完全二叉树的节点个数

普通二叉树——递归法

首先按照普通二叉树的逻辑来求。

这道题目的递归法和求二叉树的深度写法类似， 而迭代法二叉树的层序遍历.html)遍历模板稍稍修改一下，记录遍历的节点数量就可以了。代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        return getNodeNum(root);
    }

    int getNodeNum(TreeNode* node) {
        if (node == NULL) return 0;
        int leftNum = getNodeNum(node->left);
        int rightNum = getNodeNum(node->right);
        return leftNum + rightNum + 1;
    }
};

普通二叉树——层序遍历法

使用层序遍历的模板即可。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countNodes(TreeNode* root) {
        queue<TreeNode*> que;
        if (root == NULL) return 0;
        else que.push(root);
        int res = 0;
        while (!que.empty()) {
            int size = que.size();
            res += size;
            while (size--) {
                TreeNode* node = que.front();
                que.pop();
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return res;
    }
};

完全二叉树性质

首先我们需要熟悉完全二叉树的定义：完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。

img

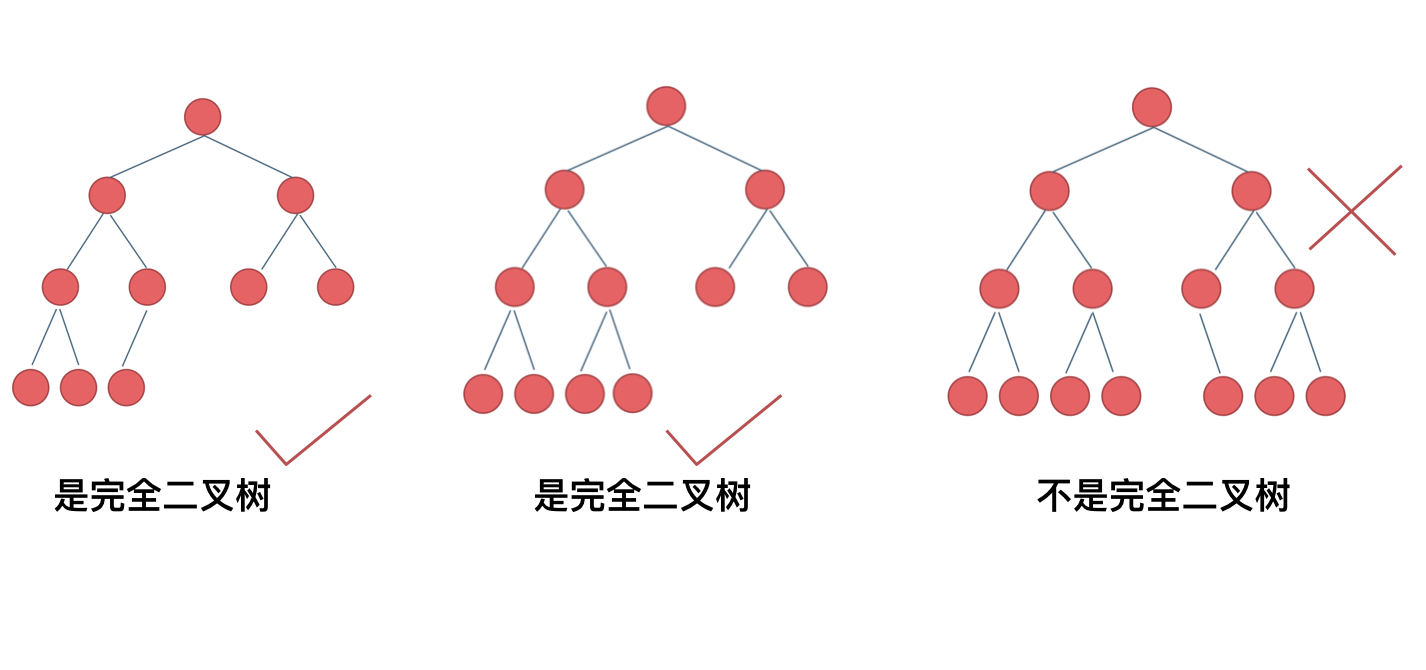
该定义表明，遍历一棵完全二叉树的左孩子节点，即可获得树根节点的深度。

int countDepth(TreeNode* node) {
        int depth = 0;
        while (node) {
            node = node->left;
            depth++;
        }
        return depth;
    }

另外还有些性质包括：

  • 满二叉树一共包含2^depth-1个节点

  • 若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

  • 完全二叉树除最底层外，上层即为满二叉树

本题解法

完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

  • 对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

  • 对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

这里我们可以对左海孩子的深度进行比较：

  • 如果根节点的左子树深度等于右子树深度，则说明左子树为满二叉树

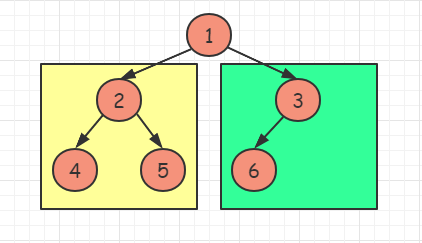
left == right

  • 如果根节点的左子树深度大于右子树深度，则说明右子树为满二叉树

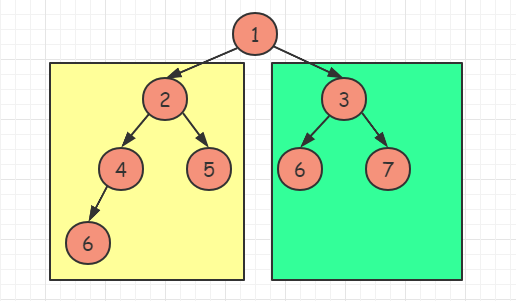
如果知道子树是满二叉树，那么就可以轻松得到该子树的节点数目，为了加快幂的运算速度，可以使用移位操作符：

(1<<depth) - 1; // depth为子树的深度；

完整代码如下：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int countDepth(TreeNode* node) {
        int depth = 0;
        while (node) {
            node = node->left;
            depth++;
        }
        return depth;
    }

    int countNodes(TreeNode* root) {
        if (root == NULL) return 0;
        int leftDepth = countDepth(root->left);
        int rightDepth = countDepth(root->right);
        if (leftDepth == rightDepth) return (1 << leftDepth) + countNodes(root->right);
        else return (1 << rightDepth) + countNodes(root->left);
    }
};

标签：node,right,TreeNode,val,int,随想录,二叉树,深度,left
From： https://www.cnblogs.com/buryinshadow/p/16961846.html

相关文章

  • 代码随想录Day36
    LeetCode235.二叉搜索树的最近公共祖先给定一个二叉搜索树,找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为：“对于有根树T的两个结点p、q，最......
  • 判断是否是完全二叉树
     对于一棵二叉树，判断是否是一棵完全二叉树。typedefstructNode{intkey;Node*lChild;Node*rChild;}*PNode;boolis(PNode&p){boolflag=false;queue<PN......
  • 一点关于深度学习实验的思考：重复实验
    前言最近做深度学习实验，时常会感叹深度学习就像炼丹一样，效果好坏似乎就像上帝在掷骰子。后面反思了一下自己的实验方法，再反思了一下做实验的目的。什么时候我们可以自信......
  • 每日算法之二叉树中和为某一值的路径(二)
    JZ34二叉树中和为某一值的路径(二)描述输入一颗二叉树的根节点root和一个整数expectNumber，找出二叉树中结点值的和为expectNumber的所有路径。1.该题路径定义为从树的......
  • 二叉树入门到进阶(下一篇讲红黑树)——c语言刷题合集
    目录二叉树概念二叉树的遍历方式DFS（前序中序后序遍历）144.二叉树的前序遍历递归解法迭代解法94.二叉树的中序遍历145.二叉树的后序遍历层序遍历--队列的作用102.二叉......
  • 代码随想录——栈与队列
    用栈实现队列题目简单把pop()和peek()中可复用的部分提取出来classMyQueue{Stack<Integer>stackIn;Stack<Integer>stackOut;/**Initialize......
  • 【论文导读】- Communication-Efficient Learning of Deep Networks from Decentraliz
    文章目录​​论文信息​​​​摘要​​​​主要内容（contributions）​​​​FederatedAveraging​​​​联邦学习​​​​隐私​​​​联邦优化​​​​联邦平均算法（FedAVG）​......
  • 深度学习中的两种anchor算法anchor-based 和anchor free 的区别
    anchor-based:这里基于fasterrcnn中选择anchor的方法##RPN阶段（anchortarget）：1.计算所有样本点(wxh)与9个anchor拼在一起形成wxhx9个框，得到all_anchors（以图像为单......
  • ChatGPT 编写的 Rust 二叉树
    //定义二叉树节点structNode{  //节点值  value:i32,  //左子树  left:Option<Box<Node>>,  //右子树  right:Option<Box<Node......
  • 代码随想录Day35
    LeetCode236.二叉树的最近公共祖先给定一个二叉树,找到该树中两个指定节点的最近公共祖先。百度百科中最近公共祖先的定义为：“对于有根树T的两个结点p、q，最近公共祖......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99