代码随想录算法训练营Day11|20. 有效的括号、1047. 删除字符串中的所有相邻重复项、150. 逆波兰表达式求值
20. 有效的括号
字符串只包括 '(',')','{','}','[',']' 这些有效字符。我们将括号分为左括号、右括号两大类。
栈结构的特殊性,非常适合对称匹配类的题目:
-
第一种情况,字符串里左方向的括号多余了 ,所以不匹配。
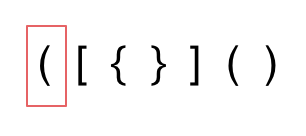
这种情况会出现字符串遍历完毕,但栈中仍剩余元素的情况。所以在遍历完成后我们需要执行
st.empty()对栈元素是否为空进行判断。 -
第二种情况,括号没有多余,但是 括号的类型没有匹配上。
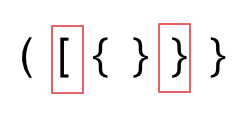
这种情况主要是括号不匹配的问题,这里我们需要根据括号种类不同分三种情况分别讨论。
-
第三种情况,字符串里右方向的括号多余了,所以不匹配。
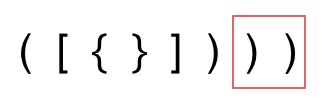
这种情况可能出现字符串未结束遍历,但栈中已不存在元素,所以遍历过程中每次从栈顶中取出元素前,也需要使用
st.empty()对栈元素是否为空进行判断。
①常规做法(复现流程)
class Solution {
public:
bool isValid(string s) {
stack<char> st;
for (char c : s) {
if (c == '(' || c == '[' || c == '{')
st.push(c);
else {
if (st.empty())
return false;
char temp;
switch (c) {
case ')' :
temp = st.top();
st.pop();
if (temp != '(')
return false;
break;
case ']' :
temp = st.top();
st.pop();
if (temp != '[')
return false;
break;
case '}' :
temp = st.top();
st.pop();
if (temp != '{')
return false;
break;
}
}
}
if (st.empty())
return true;
return false;
}
};
②剪枝+栈元素优化
首先可以取巧去人为删除一些情况,当字符串长度为奇数,必定存在至少一个符号不能匹配的情况。
if (s.size() % 2 != 0)
return false;
另外在原先的复现流程中,我们在栈中存放{、[、(,然后再将字符串中取出右括号后与相对应的左括号进行匹配。其实可以考虑直接在栈中存储左括号相应的右括号,这样遍历比较时可以直接使用==比较。代码如下:
class Solution {
public:
bool isValid(string s) {
// 先剪枝排除部分情况
if (s.size() % 2 != 0)
return false;
stack<char> st;
for (char i : s) {
// 对于'(','[','{'的情况直接插入
if (i == '(') st.push(')');
else if (i == '[') st.push(']');
else if (i == '{') st.push('}');
// 匹配前判断栈是否为空
else if (st.empty() || st.top() != i) return false;
else st.pop();
}
return st.empty();
}
};
1047. 删除字符串中的所有相邻重复项
题目中表明输入字符串只包括小写字母,并且删除操作需要重复进行。因为可能删除一次后的新字符串又出现相邻且重复的元素组成。
①递归法
栈与递归之间在某种程度上是可以转换的。因为要重复执行同一个删除操作,并且每次删除操作输入的字符串都在动态变化,所以考虑到使用递归函数。
(代码执行错误!!!)
class Solution {
public:
string removeDuplicates(string s) {
removeSingleDuplicate(s);
return s;
}
// 递归函数
void removeSingleDuplicate(string& s) {
for (int i = s.size() - 1; i > 0; i--) {
if(s[i] == s[i - 1]) {
s.erase(s.begin() + i);
cout << s << endl;
cout << s.size() << endl;
s.erase(s.begin() + i - 1);
cout << s << endl;
cout << s.size() << endl;
if (s.size() == 0 || s.size() == 1) return;
else {
removeSingleDuplicate(s);
}
}
}
}
};
而且在企业项目开发中,尽量不要使用递归!在项目比较大的时候,由于参数多,全局变量等等,使用递归很容易判断不充分return的条件,非常容易无限递归(或者递归层级过深),造成栈溢出错误(这种问题还不好排查!)
②栈——解决对称结构问题
class Solution {
public:
string removeDuplicates(string s) {
stack<char> st;
for (char i : s) {
if (st.empty()|| i != st.top()) st.push(i);
else st.pop();
}
string res = "";
while (!st.empty()) {
res += st.top();
st.pop();
}
reverse(res.begin(), res.end());
return res;
}
};
其实队列跟字符串都可以使用back()、front()函数访问字符串首尾字符,这里因为我们使用栈的原因还需要对出栈结果进行反转,可以考虑直接使用字符串进行压栈、入栈的模拟。
class Solution {
public:
string removeDuplicates(string S) {
string result;
for(char s : S) {
if(result.empty() || result.back() != s) result.push_back(s);
else result.pop_back();
}
return result;
}
};
150. 逆波兰表达式求值
可以保证给定的逆波兰表达式总是有效的。所以不需要考虑字符串的异常输入造成的问题。
由于题目测试样例的范围波动大,使用有符号整型int无法有效存储所有数值,需要修改数据类型为long int或者long long。

我们可以使用存储整型的栈,将非运算符的字符串先用stoll函数转化为数值(此处已经考虑过负数的情况),当遍历到运算符时,再根据运算符的种类做相应处理。
代码如下:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
long int res;
stack<long int> st;
for (int i = 0; i < tokens.size(); i++) {
if (tokens[i] == "+") {
long int second = st.top();
st.pop();
long int first = st.top();
st.pop();
long int temp = first + second;
st.push(temp);
}
else if (tokens[i] == "-") {
long int second = st.top();
st.pop();
long int first = st.top();
st.pop();
long int temp = first - second;
st.push(temp);
}
else if (tokens[i] == "*") {
long int second = st.top();
st.pop();
long int first = st.top();
st.pop();
long int temp = first * second;
st.push(temp);
}
else if (tokens[i] == "/") {
long int second = st.top();
st.pop();
long int first = st.top();
st.pop();
long int temp = first / second;
st.push(temp);
}
else st.push(stoi(tokens[i]));
}
return st.top();
}
};
因为弹出栈顶的代码重复度比较高,我们可以考虑先将运算符和数值进行区分,如果是运算符类别,在弹出栈顶后再根据具体运算符类型进行操作,简化代码如下:
class Solution {
public:
int evalRPN(vector<string>& tokens) {
// 力扣修改了后台测试数据,需要用longlong
stack<long long> st;
for (int i = 0; i < tokens.size(); i++) {
if (tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/") {
long long num1 = st.top();
st.pop();
long long num2 = st.top();
st.pop();
if (tokens[i] == "+") st.push(num2 + num1);
if (tokens[i] == "-") st.push(num2 - num1);
if (tokens[i] == "*") st.push(num2 * num1);
if (tokens[i] == "/") st.push(num2 / num1);
} else {
st.push(stoll(tokens[i]));
}
}
int result = st.top();
st.pop(); // 把栈里最后一个元素弹出(其实不弹出也没事)
return result;
}
};