《Zerocoin: Anonymous Distributed E-Cash from Bitcoin》论文学习笔记
@
目录【前导知识】
1.电子现金
密码货币:银行为用户对某个文件或数据做数字签名,签名的结果被赋予货币的功能。
☆ 需要解决3个问题:
1.防止重复花费
2.找零钱
3.隐私性(特殊的隐私保护)
☆特殊的隐私保护:
1.我的钱,你可见,但不能用,除非我给你了。
2.我的钱,你可见,但不知道我用到哪了
3.我的钱,我可用,但只能用一次
2.密码货币zerocoin
利用密码学技术实现:匿名性、不可公开性
铸币:相当于把电子现金兑换成zerocoin,把区块链作为“公告板”,用户可以把自己的电子现金放在公告板里面(大家都可见,也就是我的钱你可见,但是你不能用)
1. Introduction
比特币成功的原因:比特币是完全去中心化的,不需要中央银行或权威机构。相反,它的安全性依赖于分布式架构和两个假设:它的大多数节点都是诚实的,并且大量的工作证明可以阻止[Sybil攻击](https://baike.baidu.com/item/Sybil Attack/7567996?fr=aladdin)。 因此,比特币既不需要法律机制来检测和惩罚重复支出,也不需要选择、监控或监管可信的各方。但它也是有代价的:所有交易都是公开的,都是在具有密码约束力的化名之间进行的。
虽然用户使用一个地址来表示其在比特币中的身份,但是很多研究表明,能够通过交易数据挖掘和追踪用户信息,甚至能够将比特币上面的“身份”链接到现实真实身份。总结起来就是,比特币的匿名性还不够。
但是对于这个问题的解决措施十分有限,最常见的方法就是使用laundry service:通过一个第三方的混淆者,把许多用户的比特币混合在一起的服务,来达到混淆交易记录的目的,让别人看不到这个比特币到底是谁的,来达到混淆交易的目的,如下图所示:
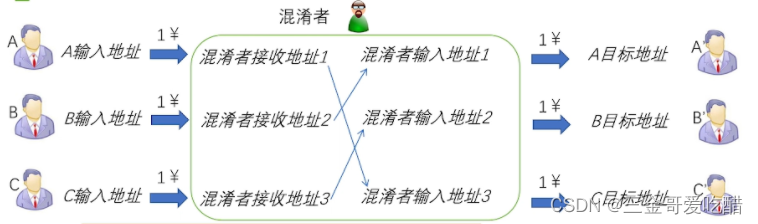
但是,这种方法也有严重的局限性:运营商可以窃取、追踪比特币,或者干脆倒闭,将用户的比特币带走。认识到这些风险,混淆服务可能会缩短混淆时间,这导致最小的交易量并因此限制了匿名性。
Our contribution
描述了ZerocoinZerocoin,这是一种分布式电子现金系统(decentralized e−cash schemedecentralized e−cash scheme)它使用密码技术来打破个人比特币交易之间的联系,而不需要添加可信的各方。要做到这一点,我们首先定义一个新原语的抽象功能和安全需求,我们称之为非集中式电子现金方案。接下来,我们提出了一个具体的实例,并证明了它在标准密码假设下是安全的。最后,我们描述了将我们的协议集成到比特币系统中所需的具体扩展,并评估了从原始开源比特币客户端派生的原型实现的性能。
我们并不是第一个提出电子现金技术来解决比特币隐私问题的人。然而,许多电子现金协议的一个共同问题是,它们基本上依赖于受信任的货币发行商或“银行”,使用盲签名方案创建电子“硬币”。而比特币网络模型由许多经常进出网络的不可信节点组成。此外,选择长期信任方的问题,尤其是在比特币运营的法律和监管灰色地带,似乎是采用比特币的主要障碍。Zerocoin通过允许个人比特币客户生成自己的硬币,从而消除了对此类硬币发行者的需求——前提是他们有足够的比特币来这么做。
2.总体思路
比特币有一个优点同时这个优点也是它的缺点,那就是它的交易数据是公开透明的,且使用UTXO模型来建模交易关系。这保证了人人都可以认证,但泄露了用户交易隐私。虽然用户使用一个地址来表示其在Bitcoin中的身份,但是很多研究表明,能够通过保存在比特币上的交易数据挖掘和追踪用户信息,甚至能够将比特币上面的“身份”链接到现实真实身份。总结起来就是,比特币的匿名性还不够。
为了解决这些问题,这篇文章提出了zerocoin,大致的思路是这样的:
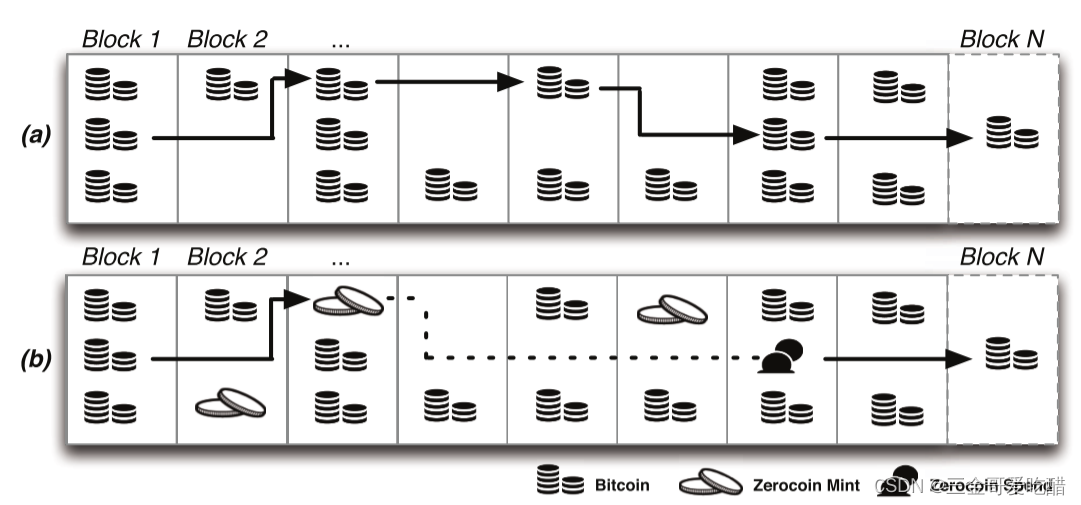
作者将图的上面部分表示在Bitcoin中的交易记录,我们可以看到,一个转账的转账者的地址和接收者的地址是能够被链接起来的。
下面部分表示的是Zerocoin的交易。它是基于比特币的,所以有一个Zerocoin Mint(把比特币/电子现金转换为zerocoin)的步骤。关键点在于图中的虚线部分,表示这两个交易不是链接在一起的,以这样的方式来匿名、防追踪。
那么把Bitcoin(电子现金)转化成zerocoin以后,钱怎么花出去呢?
大致是这样的:用累加器将可收集到的电子现金累加起来,并以零知识证明的方式证明自己的电子现金在累加器中,这样就可以实现花钱时的匿名性了(累加器中累加的就是公告板里面的电子现金,要用的时候要证明自己的钱确实是在累加器里面,所以要用零知识证明来证明一下自己的电子现金在累加器里面,这样就实现了花钱时的匿名性了)。
协议构造
1.参数产生
由一个可信的第三方执行:
Setup(1λ)→params=(x,n,p,q,g,h),其中(x,n)是RSA累加器的参数,(p,q,g,h)是Pederson承诺协议的参数。
2.铸币协议
假设Alice想把一个比特币转换成一个zerocoin,则由Bob执行:
Mint(params)→(c,S,r),随机取S,r←RZq*,计算c=gShr mod p 作为序列号为s的新币(公开),而skc=(S,r)是作为花钱时使用的秘密钥。
其中c是一个commitment(铸币承诺),也就是把自己的钱(Bitcoin)兑换成zerocoin,承诺之后就把c作为钱,这个钱是公开的,但是S是保密的,可以把S当做序列号,用来标识一个zerocoin(旷工通过检查S是否已经存在区块链中来避免一个币被二次花费的问题)。
接着,Alice需要将这个c作为一个Bitcoin交易的output,生成一个比特币交易,这样就完成了把一个比特币转换成了zerocoin。
ps:这有两个特性:
①捆绑性:知道c的值,去修改S和r是做不到的,如果想求出S和r的值,可以假设一个去求另一个,这是离散对数级别的问题,是求不出来的;
②隐藏性:由c得不出S和r,这个c就是钱(可见但没法用),但拥有这个钱的人可以用,因为知道S和r。
3.花钱协议
当Alice要花费这枚Bitcoin的时候,在本地执行:
Spend(params,c,skc,R,C)→(π,S)
其中R是接收方的公开地址,C是用户收集到的网络中公开发行的钱币集合(也就是c的集合)。
具体分为一下四步:
①计算A=RSAAccu(params,C);
②计算w=GetWitness(params,c,C);
这里w是证明钱c确实是在C里面,要想继续用这个钱的话需要产生一个证明π(用接收方的地址进行签名),因为如果这个地址不签名的话,别人就可能把地址修改了(挪用)。
③计算π=ZKSoK[R]{(S,r):AccVerify(params,A,c,w)=1∧c=gShr}
这名部分要证明两个东西:
第一,c确实是在第①步累加的A里面(要知道w);
第二,证明c确实是S和r的一个承诺
④输出(π,S),代表这笔钱已经花出去了(因为已经通过证明了),S就代表序列号,要是再用这个序列号就重复了(防止了重复花费的问题)
4.验证交易
Verify(params,π,S,R,C)→0,1
①计算A=RSAAccu(params,C);
②验证π,如果验证通过,接收者则可确认:
· C中的确包括发送者要花费的钱币;
· π中对S的承诺是正确的;
· 对R的签名是正确的。
整个证明的过程都没有出现c,所以就实现了用钱的匿名性。接收者通过花钱协议得到(π,s),由于累加器中元素的隐藏性以及π的零知识性,接收者不能得到(r,c),因此不能得知用户使用的是哪个钱。
存在的问题
zerocoin的缺点有:
1.Mint协议中得到的钱c对应系统规定的固定面值,因此缺乏灵活性;
2.系统不支持找零业务。
Mint协议其实是一个兑换协议,用比特币兑换成了zerocoin,这个钱是固定的,因此缺乏灵活性。整个过程中c直接拿出去用了,没有找零钱。而zerocash改善了这两个缺点。
标签:zerocoin,现金,Zerocoin,累加器,比特,Distributed,Cash,Bitcoin,params From: https://www.cnblogs.com/ac36/p/16867374.html