10.31
原题:gym 103495.
赛时没有看见,晚上回家补了。
A. Longest Continuous 1
考虑打表,设 \(L_i\) 表示从 \(0\) 写到 \(2^{i}-1\) 的长度之和,这个可以打一个长度为 \(30\) 的表,那么我们可以找到 \(k\) 处于哪一块,例如 \(k\in(L_{i-1},L_i]\),那么答案显然为 \((i-1)+1\) 即 \(i\),证明简单,讨论一下是否会出现两个不是 \(2^m-1\) 这样的数拼起来更大的情况。‘’
复杂度 \(\Theta(T\log 30)\)。
code。
B. Fake Walsh Transform
诈骗。
当 \(m\ge 2\) 时,\(0\) 到 \(2^{m}-1\) 所有数异或和为 \(0\),如果要得到 \(n\) 我们直接从这些数中扣去 \(n\) 就行了。所以我们可以分类讨论:
-
当 \(m\ge 2,n=0\) 时,答案为 \(2^m\)。
-
当 \(m\ge 2,n\neq 0\) 时,答案为 \(2^m-1\)。
-
当 \(m=1,n=0\) 时,答案为 \(1\)。
-
当 \(m=1,n=1\) 时,答案为 \(2\)。
复杂度 \(\Theta(T)\)。
code。
C. Magical Rearrangement
本质上是求一个字典序最小,因为每个数都得用上。那么从最高位开始贪心,每次选择一个最小的可以用上的数,并且这个数放置上去不会出现无解情况。
考虑如何判断无解。设 \(a_i\) 总和为 \(sum\),\(a_i\) 最大值为 \(m\)。考虑 \(0\) 的情况,第一个位置是不能放 \(0\) 的,所以 \(0\) 最多能放置 \(sum-a_0\) 个位置,如果 \(a_0>sum-a_0\),那么就无解。对于其它数的情况,只需要考虑最大的数 \(m\),因为既然出现次数最多的数都能放置其它数也都能放置,判断方法也是和 \(0\) 是一样的,只不过开头是可以放这个的。
复杂度 \(\Theta(100n)\)。
code。
D. Anti-merge
如果把不放置标签看做颜色 \(0\),那么根据黑白染色可知,最多只需要 \(1\) 种额外的颜色,那么我们把相同 \(a_i\) 的四联通的点连一条边,枚举一下起始点的颜色取最优即可。
复杂度 \(\Theta(n+m)\)。
code。
11.1
期望 \(100+80+65+30=275\)。
实际 \(90+60+35+30=215\)。
A. 区间检测
\(m\) 次询问区间是否有重复的数。
\(1\le n,m\le 10^6\),\(0\le a_i\le 10^9\),时限 \(\text{200ms}\)。
赛时写了一个整体二分 \(O(n\log n+m)\) 的 sb 做法,虽然与正解同复杂度,但是以 \(\text{204ms}\) 的好速度压线 \(\text{TLE}\)。
设 \(r_i\) 表示 \(i\) 左边第一个与 \(a_i\) 相等的数,然后这个东西显然可以尺取来做,但是值域在 \(10^9\) 非常难受,但是我们有 \(\texttt{bitset}\) 这个空间 \(O(\frac{n}{32})\) 的好东西。把 \(r_i\) 做一个前缀 \(\max\) 即可。
code。
B. 新能源汽车厂
维护两个序列 \(a,b\),每次将 \(a\) 进行区间加,或对 \(b\) 进行区间推平,每次操作后求 \(\sum_{i=1}^na_ib_i\)。
\(1\le n,q\le 10^5\),\(1\le a_i,b_i\le 10^4\)。
直接用线段树维护 \(a,b\) 的区间和,以及区间的答案,打标记直接下传就行了,甚至不需要规定顺序。
复杂度 \(O(n\log n+q\log n)\)。
code。
C. 旅行
给定 \(n\) 个点 \(m\) 条边的 DAG,每个点有一个物品,重量 \(w_i\),价值 \(v_i\),背包重量上限 \(W\),若背包当前重量 \(a\),走过边权 \(b\),则需要花费 \(a\times b\) 的体力。求价值最大的情况下体力最小。
\(1\le n,W,v_i,w_i\le 10^3\),\(1\le m\le 2\times 10^4\),\(0\le z_i\le 10^3\)。
用 \(f_{i,j}\) 保存二元组 \((a,b)\),表示考虑到了第 \(i\) 个点,背包重量为 \(j\),最大价值以及最少体力分别是多少。
对于一条 \(x\to y\) 的边,边权为 \(z\),若不选 \(y\) 这条边,那么直接把这一条边需要的体力算进去;否则做一次 01 背包就行了。
注意我们在做拓扑之前需要把无用的边去掉,重新计算入度。
code。
D. 远离班主任
给定 \(n\) 个节点的数,\(q\) 次询问,每次给定两个点 \(x,y\),求 \(\max_{1\le i\le n}\{\min\{d(i,x),d(i,y)\}\}\)。
\(1\le n,q\le 10^5\)。
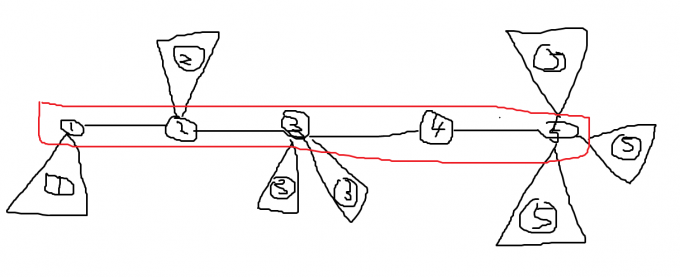
我们把直径先抽出来,对于直径上点从左往右进行 \(1,2,3,\cdots,K\) 的编号,设 \(i\) 点编号为了 \(idx_i\),两点编号之差即为距离。
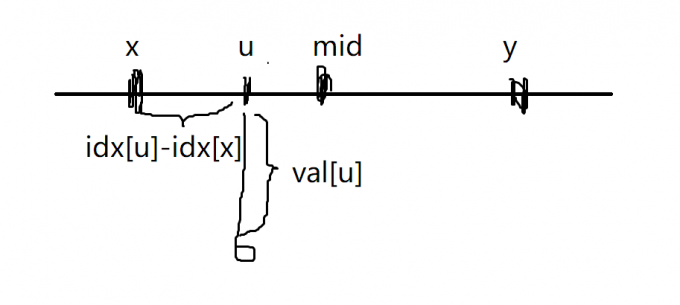
对于一个直径上的点 \(u\) 延伸出来的子树,我们同样将子树内每一个点都标号为 \(idx_u\)。显然只有子树中距离 \(u\) 最远的点才可能对答案产生贡献,我们记这个距离为 \(val_u\),同时,我们还要记录一下子树中每一个点 \(v\) 到 \(u\) 的距离 \(dis_v\),方便之后的处理。这个图可能会形象一点:
考虑一组询问 \((x,y)\),如果 \(x,y\) 在直径上某一点的子树内,那么成为答案的只有可能是直径两端点中的某一点,因为,如果某一点距离 \(x\) 或 \(y\) 比直径端点还要远,那么那个点就会成为直径。所以我们只需要计算直径两端点与 \(x,y\) 的 \(dis\) 较小点距离最大值即可,答案为 \(\max(idx_x-1,K-idx_x)+\min(dis_x,dis_y)\),注意这里 \(idx\) 减一的原因是我们从 \(1\) 开始标的号,所以算距离需要减一个 \(1\)。
如果 \(x,y\) 不在同一子树内,先考虑一个简单情况,\(x,y\) 均在直径上。
考虑计算出 \(x,y\) 的中间点 \(mid\),显然,\(mid\) 左边的点都会跑去 \(x\),右边的点都会跑去 \(y\),对于 \([x,mid]\) 这一段上某个节点 \(u\),在开头已经说了,只需要考虑最远节点的距离,那么 \(u\) 的贡献为 \(val_u+idx_u-idx_x\)。对于 \([mid,y]\) 这一段上的点也是同理的,画个图更容易理解,贡献为 \(val_u-idx_u+idx_y\)。
我们发现,两种情况其实就是求区间 \([l,mid]\) 和 \((mid,r]\) 的 \(idx_u+val_u\) 或者 \(idx_u-val_u\) 的最大值,使用 ST 表可以做到 \(O(1)\) 的回答。另外不要忘记还得再计算直径两端点的贡献,即计算两端点到 \(x,y\) 距离最小值的最大值,与上面的情况取 \(\max\) 即可。
\(x,y\) 不在直径上的情况其实已经解决了,每一个点 \(u\) 的贡献只要加上偏移量 \(dis_x\) 或 \(dis_y\) 就行了。
code。
11.4
期望:\(60+100+100+20=280\)。
实际:\(60+100+100+20=280\)。
A. 01完美矩阵
给定 \(n\times m\) 的 01 矩阵,求有多少个四边都为 \(1\) 且大小至少为 \(2\times 2\) 的矩阵,满足内部 \(0\) 与 \(1\) 数量差不超过 \(1\)。
\(1\le n,m\le 300\)。
收获到了矩阵计数的套路。枚举上下边界,扫一遍列,用前缀和维护。
具体的,我们枚举一段上下界全部为 \(1\) 的连续区间,然后扫一个右竖线,当这个竖线上也全是 \(1\) 时,考虑统计出右竖线左边形成的矩阵中 \(0\) 和 \(1\) 的数量之差,记为 \(M\),那么现在只需要统计出,右竖线左边有多少个竖线,满足这个竖线左边 \(1\) 与 \(0\) 的数量差 \(M'\) 满足 \(|M-M'|\le 1\)。这个很好实现,我们只需要做一下每条竖线的贡献的前缀和即可。
code。
B. 天天爱消除
有 \(4\) 种颜色的消消乐,最少多少次消完。
\(2\le n,m\le 6\)。
搜索剪枝可过,没什么好说的。
code。
C. 树上的环
原题:CF629E。
若 \(A\) 为所有环的长度之和,\(B\) 表示有多少种可能的环,那么答案为 \(\frac{A}{B}\)。
设 \(x\) 为询问中深度较小点,\(y\) 为深度较大点。对于 \(x\) 不是 \(y\) 的祖先的情况,那么 \(x\) 子树内每一个点都可以和 \(y\) 子树内每一个点进行匹配,我们把路径长度分为三部分。第一部分 \(x\) 子树内一点到 \(x\) 的路径和,第二部分 \(y\) 子树内一点到 \(y\) 的路径和,第三部分子树内的点经过 \(x,y\) 到 \(\text{LCA}\) 的路径和。\(O(\log n)\) 的时间内求出 LCA 后可以很轻松地维护。
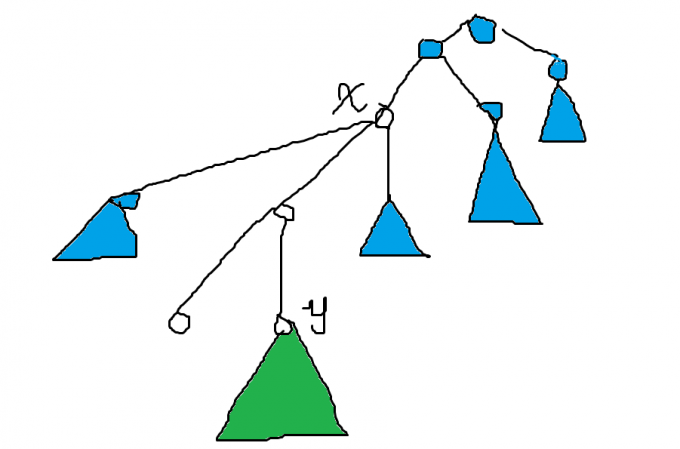
若 \(x\) 是 \(y\) 的祖先,我们可以把贡献画一张图考虑:
我们把贡献同样分成三部分,第一部分是绿色部分到 \(y\) 的路径和,第二部分是蓝色部分到 \(x\) 的路径和,第三部分是绿色与蓝色两两连边的长度和。
蓝色部分的大小是好求的,我们只需要求 \(y\to x\) 路径上 \(x\) 的儿子,记为 \(son\),这个可以倍增,然后第一部分和第三部分就非常容易了。
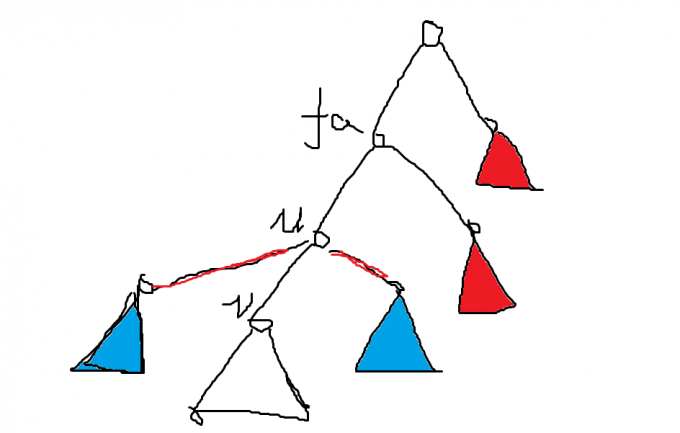
第二部分考虑贡献可以写成 \(S\times d_u+\sum_{x\in \text{blue}}d_x-2d_{\operatorname{lca}(u,x)}\),\(S\) 表示蓝色部分的大小,那么我们可以设 \(f_{son}\) 表示 \(\sum_{x\in \text{blue}}d_x-2d_{\operatorname{lca}(u,x)}\) 这个贡献。考虑下面这张图:
\(f\) 的求法可以做一个简单的换根,二次扫描一下,设 \(v\) 的父亲为 \(u\),我们先令 \(f_v\leftarrow f_u\),对于 \(d_x\),我们应加上蓝色区域每个点的贡献,即深度之和,我们记 \(sum_x\) 表示 \(x\) 子树内每个点的深度之和,那么蓝色部分的贡献为 \((sum_u-sum_v)\)。然后考虑 \(2d_{\operatorname{lca}(u,x)}\),注意到红色部分的子树是无需考虑的,因为 \(2d_{\operatorname{lca}(u,x)}\) 的贡献没有变,即对于原来 \(u=fa\) 时,红色部分与 \(u\) 的 LCA 和当前 \(u\) 与红色部分的 LCA 是一样的,我们还是只需要考虑蓝色部分的贡献,注意到 LCA 的取值肯定为 \(u\) 所以贡献为 \(2\times d_u\times (siz_u-siz_v)\)。
然后就做完了,复杂度 \(O(n\log n+m\log n)\)。瓶颈在处理 LCA,可以考虑使用四毛子让复杂度变成线性(
code。
D. 函数返回值
题意.
考虑没有字母怎么做,显然每一个循环互不影响,答案为 \(\prod_{i=1}^n\left(Y_i-X_i+1\right)\)。
这个部分分可以启示我们,把循环分成若干组,不在同一组的两个循环互不影响,若第 \(i\) 组的答案为 \(S_i\),则总答案为 \(\prod_i S_i\)。
\(S_i\) 的求法可以考虑把相互影响的循环连边,建一张图出来。比如 \(X_i=\texttt{'c'}\) 或 \(Y_i=\texttt{'c'}\),那么我们就将 \(i\) 与 \(3\) 之间连一条双向边。注意到,由于数据保证 \(X_i\) 和 \(Y_i\) 只有一个字母,所以每个点往前连一条边,得到的图实际上是一个森林,答案即为每棵树的答案的乘积。
我们对每棵树进行树形 dp,我们发现,若 \(u,v\) 的父亲是 \(x\),那么 \(u,v\) 对应循环的枚举是互不干涉的,所以也可以将 \(x\) 的每一个儿子的答案乘起来。
设 \(f_{u,j}\) 表示 \(u\) 节点对应的循环,下标恰好等于 \(j\) 时的答案,那么显然有状态转移方程 \(f_{u,j}=\prod_{v\in\operatorname{son}(u)}\left(\sum_{k\in S}f_{v,k}\right)\),其中 \(S\) 表示的是,当 \(u\) 对应循环枚举到 \(j\) 时,\(v\) 对应的循环可以枚举哪些数。
然后我们对每一个节点的 dp 值处理一下前缀和即可,复杂度 \(O(nV)\)。
code。
11.5
期望:\(100+100+0+20=220\)。
实际:\(100+80+0+20=200\),\(rk18\)。
A. 幸运数字
单点修改,区间查询子段和 \(\bmod 3\) 为 \(0\) 的数量。
\(1\le n,m\le 10^5\)。
我们维护模 \(3\) 意义下的前缀和,那么值相同的前缀和可以两两匹配。
那么我们用线段树维护区间前缀和 \(\bmod 3\) 分别等于 \(0,1,2\) 的数量,单点修改就变成了区间加,然后乘法原理即可。
时间复杂度 \(O(n\log n+m\log n)\)。
code。
B. 比赛
给定 \(n\) 个点的树,终点为 \(1\) 号点,\(m\) 种路线,每个路线可以提供从 \(x_i\) 开始 到 \(1\) 路径上连续的 \(k_i\) 条边,花费为 \(v_i\),\(q\) 次询问,每次询问 \(x\) 到 \(1\) 号点的最小化费。
\(1\le n,m\le 2\times 10^5\),\(1\le V\le 10^9\)。
dp 转移方程显然,设 \(f_i\) 为从 \(i\) 到 \(1\) 号点的最小花费,则 \(f_i=\min_{j\in S_k}\{f_j\}+v_k\),其中 \(S_k\) 表示用第 \(k\) 种地图 \(i\) 能到达的点集,\(v_k\) 表示第 \(k\) 种地图的花费。
这个过程显然可以用倍增优化处理,时间复杂度 \(O(n\log n+q)\)。
C. 商务 party
原题。
神仙题,不会。
D. 圣杯战争
原题。
神仙题,不会。
11.7(上午)
期望:\(100+100+100+0=300\)。
实际:\(100+100+100+0=300\),\(rk1\)。
A. Mr. Kitayuta's Colorful Graph
暴力题。
对于每一次询问,枚举一个颜色 \(c\),把颜色为 \(c\) 的边加入到并查集中,然后判断 \(u_i\) 和 \(v_i\) 是否联通即可。
时间复杂度 \(O(nmq)\)。
code。
B. Mr. Kitayuta, the Treasure Hunter
很容易与根号联想到,这道题中步数的变化显然不会超过根号。
设 \(f_{i,j}\) 表示走到第 \(i\) 个点,上一次用了 \((d+j)\) 步,所能获得的最大收益,其中 \(j\in [-\sqrt{n},\sqrt{n}]\),需要加一个常数放置越界。
code。
C. Mr. Kitayuta's Technology
连通块的贡献相互独立,所以可以只对一个连通块进行考虑。
对于一个 \(k\) 个点的连通块,如果它是一个 \(\texttt{DAG}\),那么类似最小生成树,我们只需要 \((k-1)\) 条边。
如果它包含环,那么显然需要 \(k\) 条边,因为多保留环上的一条边,而如果它包含强联通分量,我们可以把强联通分量上的点连成一个环,答案同样为 \(k\)。
所以说,如果令 \(x\) 为 \(\texttt{DAG}\) 的数量,那么我们需要 \(n-x\) 条边。直接做是不好做的,但是注意到 \(\texttt{DAG}\) 的数量即为连通块的数量减包含强联通分量的连通块数量。
前者我们用并查集实现,后者可以对图进行拓扑排序,没有拓展到的点即为环上的点。
时间复杂度 \(O(n+m)\)。
code。
D. Mr. Kitayuta vs. Bamboos
牛逼题。
如果正着做,每轮操作 \(h_i\) 都需要对 \(0\) 取一个 \(\max\),这是不好处理的,但是我们反着做,就可以把一个条件性的问题转成操作化的问题。
具体地,我们可以二分答案一个 \(L\),表示 \(m\) 轮操作后 \(h_i\) 的最大值,最坏的情况打算,假设这 \(n\) 棵竹子的高度都为 \(L\),那么问题就变成,每次每个数都会减去 \(a_i\),然后你可以选择 \(k\) 个数加上 \(p\)。你需要保证任何时候 \(\forall i\in[1,n]\),满足 \(h_i\ge 0\),问 \(m\) 轮操作后,竹子的高度是否都 \(\ge h_i\)。
这就把 \(\max(h_i-p,0)\) 这个可能会也可能不会进行的东西,转化成,我们要去做操作,使得它不会进行,就相当于抓住了主动权!
那么这就可以贪心,我们对于每个竹子处理出,不对它进行拔高,多少天高度会小于 \(0\),那么我们每次取缩短最快的竹子进行拔高即可,这个可以用一个优先队列来维护。
时间复杂度 \(O\left(\left(n+mk\right)\log V\log n\right)\)。
code。
标签:10,code,log,noip,复杂度,NFLS,le,100,集训 From: https://www.cnblogs.com/UperFicial/p/16866950.html