posted on 2022-08-12 14:14:05 | under 模板 | source
感谢讲师 LQS 带来的网络流专题。
本文非常不严谨,请不要把它当作入门博客。
0xFF 目录
- 0x00 网络流及求法
- 0x10 网络流基本套路
- 0x11 常见 trick
- 0x12 最小割及应用
0x00 网络流及求法
网络是一张边带权的有向图,这是一个例子:
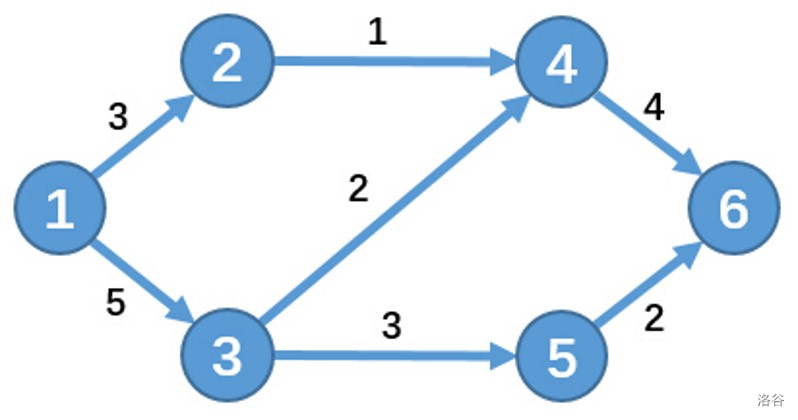
其中有一个源点 \(S\),一个汇点 \(T\)。流量从 \(S\) 源源不断地流出,每条边可以承载边权这么多的流量,每个点(除了 \(S,T\))要把它接受的流量全部流出(不能剩余),最后汇集到 \(T\),就像一个排水系统在工作。
我们将最后到达 \(T\) 的最大流量称为这个网络的最大流(Maxinum Flow)。
如果边上还有一个费用,每有一个流量流过都要支付这么多费用,最后使 \(T\) 接受最大流量的前提下,所使用的最小费用,称作这个网络的最小费用最大流(Mininum Cost & Maxinum Flow)。
0x01 暴力最大流:Ford-Fulkerson 算法
我们有一个 naive 的想法:每次从 \(S\) 发出一个流量,让它一直流到 \(T\),直到它不能流为止。在流的过程中,每流过一条边,我们就减少这条边的容量,避免下次流爆这条边。
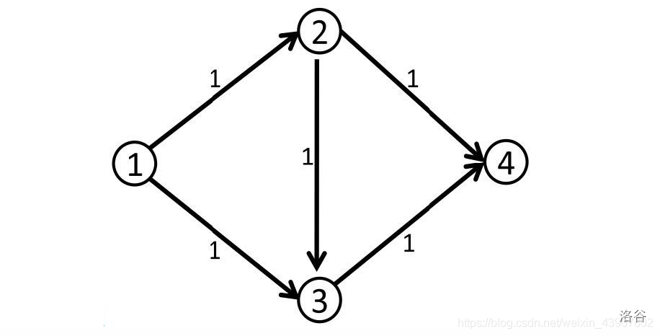
Hacked!如果我们不幸访问了 \(1\to 2\to 3\to 4\),你就寄了。明明有 \(maxflow=2\),我们却只有 \(1\),到底是什么地方出了问题?
观察到,不一定每条路径流过去都是最优的,那么我们加一条反悔边:当一条边 \((u,v)\) 流过了 \(w\) 的流量,我们就添加一条反向边 \((v,u)=w\)。如果以后我们发现走 \((u,v)\) 是不优的,我们就反悔,把这条路径分裂开,但是最大流不变。例如:
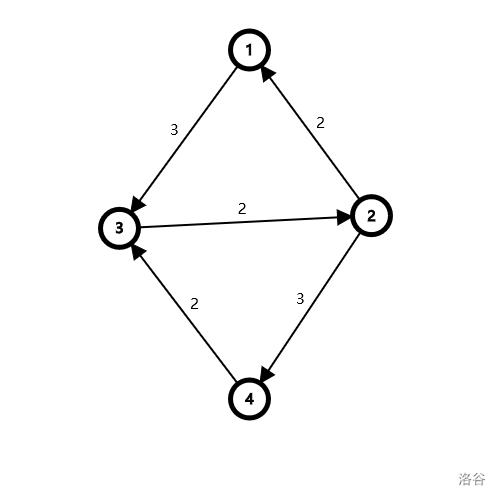
想象我们已经流了两个流量 \(1\to 2\to 3\to 4\),加上 \((2,1),(3,2),(4,3)\) 这些反悔边。现在试图走 \(1\to 3\to 2\to 4\),有了这个反悔边就可以成功流两个流量,现在真实的路径已经成为了 \(1\to 3\to 4\) 和 \(1\to2\to4\),达到了 \(maxflow=4\)。再来一个:
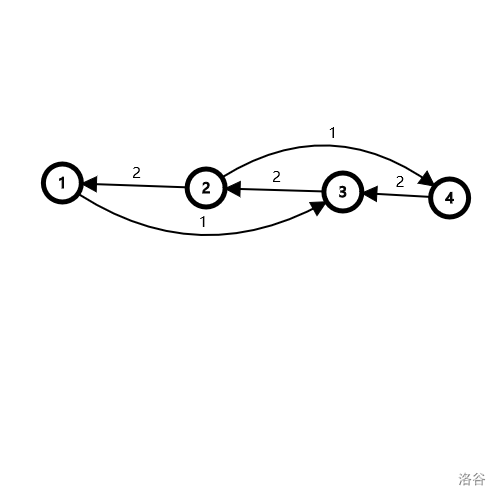
我们走了 \(1\to2\to3\to4\) 流了两个流量,现在试图走 \(1\to3\to2\to4\),是可以走过去的,且 \((3,2)\) 的反悔边没反悔完,所以最后实际上是拆成三条路径 \(1\to2\to3\to4\) 和 \(1\to3\to4\) 和 \(1\to 2\to 4\),最终 \(maxflow=3\)。
总而言之,它是正确的!于是我们可以开始模拟这个过程,得到了 FF 算法,它的复杂度是 \(O(Fm)\) 其中 \(F=maxflow\)。这样的复杂度随便卡。
0x02 最大流:Edmord-Karp 算法
为什么 FF 算法这么慢?
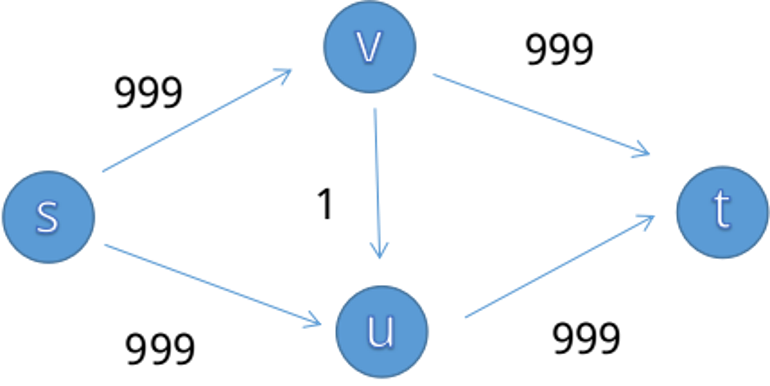
考虑优化一下,每次不要流一个流量这么少,我们使用 BFS,随便找一条路径,记录一路上最小的容量(不要走没有容量的边,可以当作不存在),再倒着回去流过来,这就是 EK 算法。复杂度 \(O(nm^2)\) 但跑不满。
0x03 最大流:Dinic 算法
为什么 EK 算法慢?我们发现,EK 一次只增广一条路径。考虑多条路径同时增广,我们先把图变成 DAG,一种可行的方法是求出每个节点的深度(BFS),增广时只走 \(dep_v=dep_u+1\) 的边,这样就没有环了,于是可以这样模拟增广的过程。
这就是 Dinic 算法,复杂度 \(O(n^2m)\)。为了吊打 EK,我们可以加入一些优化:
优化 1:当前弧优化
首先放一下原始代码:
LL dfs(int u,LL flow,int t){
if(u==t||!flow) return flow;
LL rest=flow;
for(int i=g.head[u];i;i=g.nxt[i]){
int v=g[i].v;
if(!g[i].v||dep[v]!=dep[u]+1) continue;
if(LL ans=dfs(v,min(rest,g[i].w),t)){
g[i].w-=ans,g[i^1].w+=ans;
rest-=ans;
if(!rest) break;
}
}
return flow-rest;
}
注意到一个点是会被重复走的(DAG),考虑第一次访问点 \(u\),它会放掉一部分流量给下一些点 \(v\),这些点 \(v\) 显然已经流完了,再给他们流量是没有意义的,所以第一次点 \(u\) 访问过的点 \(v\) 不需要再走,可以跳过。实现到代码里就是加一个 &,跳下一条边的同时删边。
注意,当前弧优化要把 if(!rest) break; 移到 if 里面,这条边可能没有流满,下一次仍要访问。
优化 2:炸点优化
考虑一个点 \(u\),它真的流不出流量,重复访问它是没有意义的,这时我们可以把这个点炸了,当它不存在。
0x04 最小费用最大流:EK/Dinic + SPFA = SSP
现在我们加入了费用!
怎么反悔?反悔可以理解成退钱,所以我们反悔可以把之前给的钱减掉,用一个负数即可。
考虑继续使用 EK 算法,现在我们不仅要管流量,还要管费用。可以贪心地选一条 \(S\to T\) 的最短路,把流量从这条最短路流过去,这就是最小费用最大流。
注意到费用可能为负(你自己定义的反悔边),可以使用 Bellman-Ford,复杂度是窒息的 \(O(Fnm)\)。如果有负环,SSP 将直接去世,需要消圈算法。
code EK + SPFA
template Dinic + SPFA
0x05 最小费用最大流:Dinic + Johnson 最短路 = 原始对偶
回忆一下我们怎样在负权图上跑 Dijkstra。
Recall:Johnson 全源最短路
首先我们跑一次 Bellman-Ford,判一下有没有负环,同时求出点 \(S\) 到点 \(u\) 的最短距离 \(h_u\)(距离定义为每条边的费用)。接下来是关键:将边 \((u,v)=w\) 的权值重定义为 \(w+h_u-h_v\)。最后跑 Dijkstra,所有 \(dis_u\) 更改为 \(dis_u-h_S+h_u\)。有几个问题:
为什么这些边有非负边权?考虑 \(h_u\) 是最短路长度,根据三角形不等式有 \(h_u+w(u,v)\geq h_v\),移项有 \(w(u,v)+h_u-h_v\geq 0\),证毕。
为什么最终答案为 \(dis_u-h_S+h_u\)?考虑这其实是错位相减,对于一条路径,前面的 \(-h_v\) 被后面来的 \(+h_u\) 抵消,最后剩下 \(h_S-h_u\),我们减掉这一部分就好了。
回到网络流
现在我们会了 Johnson,有个问题是怎么更新 \(h_u\),可以用这一次跑出来的最短路更新(\(h_u=dis_u-h_S+h_u\),注意到 \(h_S=0\))。考虑套上 Dinic,多路增广在最短路图上进行。我们需要换一下炸点优化,当前点 \(u\) 在栈里的时候炸掉它(\(vis_u=1\)),最后访问完再重构它(\(vis_u=0\)),如果它真的流不出去,炸了,这样就正确了。
细节
在最短路图上要怎么判断呢?如果先写 for(int i=1;i<=n;i++) h[i]+=dis[i];,那就要写 \(w(u,v)+h_u-h_v=0\) 为在最短路图上。原来是 \(dis_u+w(u,v)+h_u-h_v=dis_v\),移项并合并同类项后就是这个式子。
复杂度 \(O(Fm\log m)\),但实际表现不是很好(太长了)。
说句闲话,SSP 和原始对偶的区别在于最短路的求法,与增广路算法无关。应该是的。
0x10 网络流基本套路
作为一种模型,网络流有非常多的应用。
0x11 常见 trick
- 多源汇:建立超级源点和汇点。
- 点 \(u\) 自带流量 \(w\):连边 \((S,u)=w\)。
- 点 \(u\) 最终需要接受流量 \(w\):连边 \((u,T)=w\)。
- 经过点 \(u\) 有容量限制 \(w\):将这个点拆成 \(u,u'\),一个入点(连边 \((v,u)\)),一个出点(连边 \((u',v)\)),中间连 \((u,u')=w\)。
- 无向图:连两条有向边,现在你有了四条边哦。
0x12 最小割及应用
在网络图 \(G=(V,E)\) 中,割被定义为一种点集的划分方式:将所有的点划分成两个集合 \(s,t\),满足 \(s\cup t=V,s\cap t=\varnothing,S\in s,t\in T\)。这个割的权值被定义为 \(\forall(u,v)\in E,u\in s,v\in t\) 的 \(w(u,v)\) 之和。
最大流-最小割定理:在任意网络中,最大流等于最小割。
证明
我们记最大流是 \(\max flow\),最小割为 \(\min cut\)。根据常识:
\[\max flow=\min cut\Leftrightarrow \begin{cases} \max flow\leq \min cut\text{ (I)}\\ \max flow\geq \min cut\text{ (II)}\\ \end{cases}\]对于 \(\text{(I)}\) 式:对于任意一个割 \(cut\),最大流不会超过这个割的权值(权值是容量,不能比容量还大),所以 \(\max flow\leq cut\Rightarrow\max flow\leq \min cut\)。
对于 \(\text{(II)}\) 式,对于一个最大流 \(flow\),在残量网络上 \(S,T\) 必然不连通(否则 \(flow\) 不是最大流),我们把导致不连通的边(满流的边)拿出来做一个割,则割的权值不超过最大流,即 \(\max flow\geq cut\Rightarrow\max flow\geq \min cut\)。
所以 \(\max flow=\min cut\),证毕。
方案
用你喜欢的最大流算法跑出一个最大流,沿着残量网络从 \(S\) 找到的点就属于点集 \(s\)。
注意,最大流和最小割只有数值相等的关系(正如 SAM 和后缀树只有形态相似的关系),建最小割的图时不能按照网络流思想建。
模型 1:两者选其一
考虑你有 \(n\) 个变量 \(x_u\),第 \(u\) 个变量有 \(m\) 种取值 \(x_u=c_{u,i}\),每一个取值就是它的代价。当一个变量取到某些值时,在给另一个变量取另一些值时要多给一些代价(当 \(x_u=c_{u,i}\) 时,若 \(x_v=c_{v,j}\),则要多支付一定的代价)。这就是“两者选其一”模型。不如叫它“多者取其一”?
建图方法:想象有 \(n\) 条链,每条链有 \(m\) 条边,第 \(u\) 条链的第 \(i\) 条边是 \(c_{u,i}\),两种:
- 如果选了 \(c_{u,[1,i]}\) 再选 \(c_{v,[j,n]}\),连边 \((c_{u,[1,i]},c_{v,[j,n]})=w\)(如果不能选就是 \(\infty\))。常见变种:建一条反链,两个区间重叠,无向边等等。
- 如果物品不止一个,新建一个点 \(p\),连边 \((p,T)=w\),将限制的 \(u\) 连边 \((u,p)=\infty\)。