考虑将问题抽象成:左上角为 \((0,0)\)、右下角为 \((n,m)\) 的网格图,求所有满足至少有一条 只向下或向右走的路径 经过点集内所有点的的不同的点集大小之和。
显然对于一个合法的点集,经过它的路径可能不止一条,去重也很麻烦。考虑钦定两个点间的访问顺序,比如先向下再向右走,这样对于每个合法的点集,都有且仅有一条经过它的路径。
将路径的 拐点 分为两类:先向右再向下和先向下再向右。如下图,红色点表示第一类拐点,蓝色点表示第二类拐点。
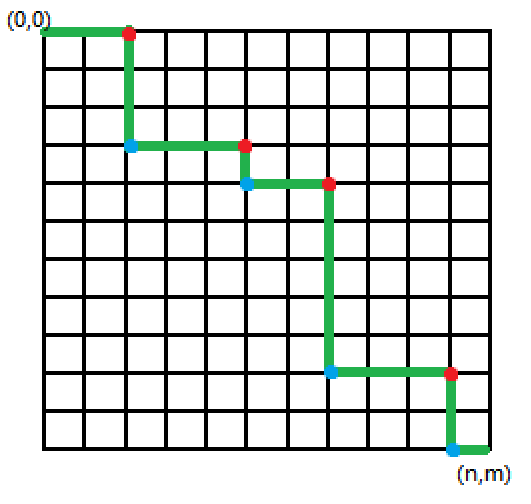
考虑 枚举先向右再向下的拐点个数 ,设有 \(i\) 个。选择拐点的方案为 \(\dbinom{n}{i}\dbinom{m}{i}\)(纵坐标范围 \([0,n-1]\),横坐标范围 \([1,m]\))。这样就唯一确定了一条路径。路径上还有 \(s=n+m-i-1\) 个点,这 \(i\) 个点可以任选,总贡献为 \(\sum\limits_{j=0}^s \dbinom{s}{j}(i+2+j) = (i+2)2^s + \sum\limits_{j=0}^s \dbinom{s}{j}j\)。
考虑 \(\sum\limits_{j=0}^s \dbinom{s}{j}j\) 这部分如何快速计算。注意到 \(\sum\limits_{j=0}^s \dbinom{s}{j}j = \sum\limits_{j=0}^s \dbinom{s}{j}(s-j)\),相加再除以 \(2\) 后得原式 \(= s2^{s-1}\)。
code
/*
p_b_p_b txdy
AThousandSuns txdy
Wu_Ren txdy
Appleblue17 txdy
*/
#include <bits/stdc++.h>
#define pb push_back
#define fst first
#define scd second
#define mems(a, x) memset((a), (x), sizeof(a))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef long double ldb;
typedef pair<ll, ll> pii;
const int maxn = 10000100;
const int N = 10000000;
const ll mod = 1000000007;
ll qpow(ll b, ll p) {
ll res = 1;
while (p) {
if (p & 1) {
res = res * b % mod;
}
b = b * b % mod;
p >>= 1;
}
return res;
}
ll n, m, fac[maxn], ifac[maxn], pw[maxn];
void init() {
fac[0] = pw[0] = 1;
for (int i = 1; i <= N; ++i) {
fac[i] = fac[i - 1] * i % mod;
pw[i] = pw[i - 1] * 2 % mod;
}
ifac[N] = qpow(fac[N], mod - 2);
for (int i = N - 1; ~i; --i) {
ifac[i] = ifac[i + 1] * (i + 1) % mod;
}
}
inline ll C(ll n, ll m) {
if (n < m || n < 0 || m < 0) {
return 0;
} else {
return fac[n] * ifac[m] % mod * ifac[n - m] % mod;
}
}
void solve() {
scanf("%lld%lld", &n, &m);
ll ans = 0;
for (ll i = 0; i <= min(n, m); ++i) {
int s = n + m - i - 1;
ans = (ans + C(n, i) * C(m, i) % mod * (pw[s] * (i + 2) % mod + (s - 1 >= 0 ? s * pw[s - 1] % mod : 0)) % mod) % mod;
}
printf("%lld\n", ans);
}
int main() {
init();
int T = 1;
scanf("%d", &T);
while (T--) {
solve();
}
return 0;
}