首页 > 其他分享 >插头DP记录

插头DP记录

时间：2025-01-15 20:00:01浏览次数：1  
标签：插头 p2 p1 pw val 记录 int DP

AAA黑题批发。

这个东西好像设问还挺广泛的，做到哪写到哪吧。

得先了解一下轮廓线dp定义。

概念

设问广泛但是总体来说是连通性相关状压dp的一类设计方法。

骨牌覆盖问题

比如说，最简单的，问你 \(n*m\) 的棋盘格里能放多少 \(1*2\) 的骨牌。

考虑把一个节点分为上下左右四个插头，从上往下，从左往右地逐格dp方案。这些插头的作用是：两个插头可以拼到一起形成一个骨牌，进而终态方案不能存在落单的插头（要不然就是 1*1 的骨牌碎片了hh）。

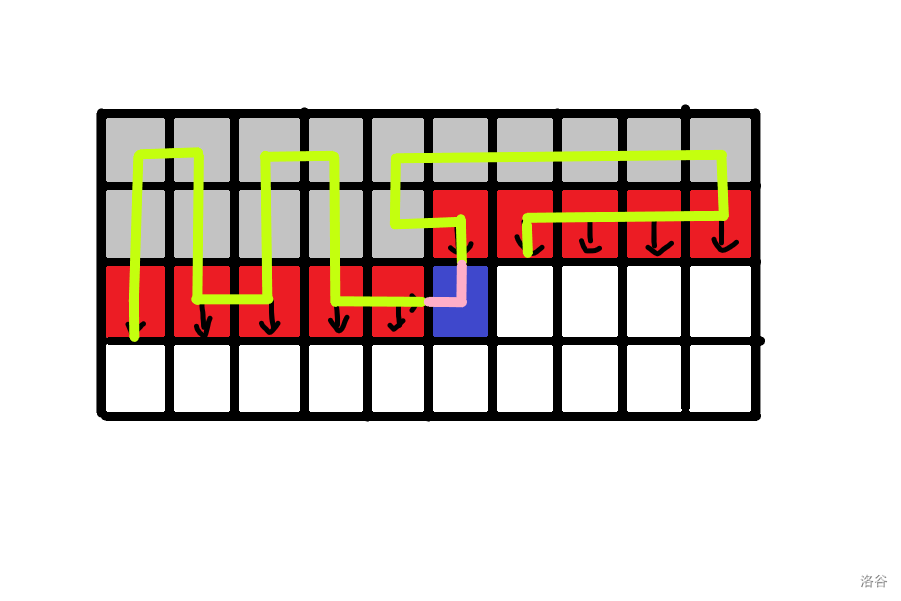
然后dp的过程是这样的。(来自luogu题解)

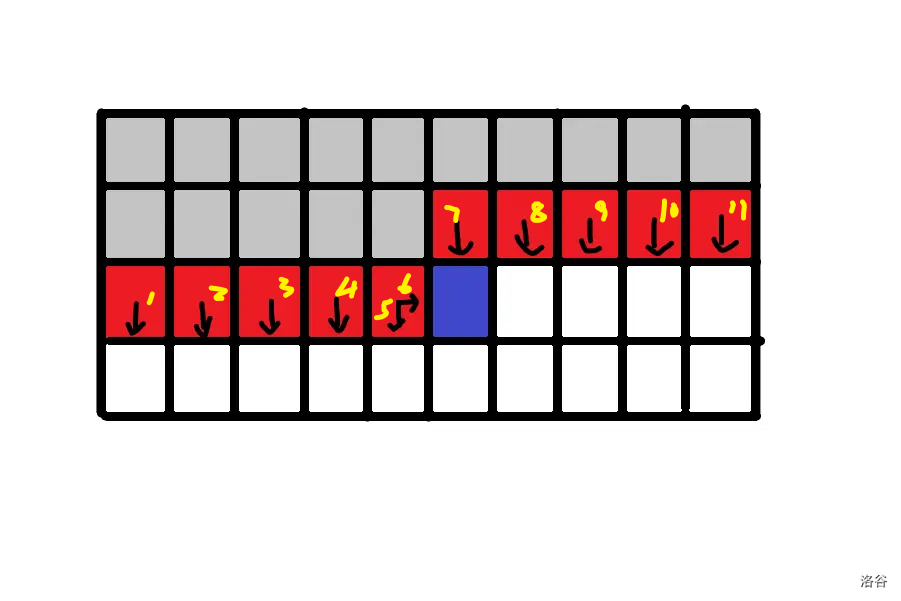
这些下箭头和那个右箭头从左到右编号为 \(1...m+1\)，蓝格子是当前考虑放置的格子 \((i,j)\)，关乎这个格子的两个插头分别是格子旁边的右插头 \(j\) 和格子上面的下插头 \(j+1\)，这张图展示的是插头的编号，实际转移中只有穿过当前轮廓线的插头才是切实存在的。

考虑状态设计 \(dp_{i,j,S}\) 表示到格子 \((i,j)\) ，当前轮廓线上的插头存在状态 \(S\)，因为当前每个插头只有存在 1 和不存在 0 所以用二进制数存储（以后会有更多进制）。

上面说到关乎当前格子的两个插头在完成当前格子的转移后格子会右移，此时右插头的编号就会变。

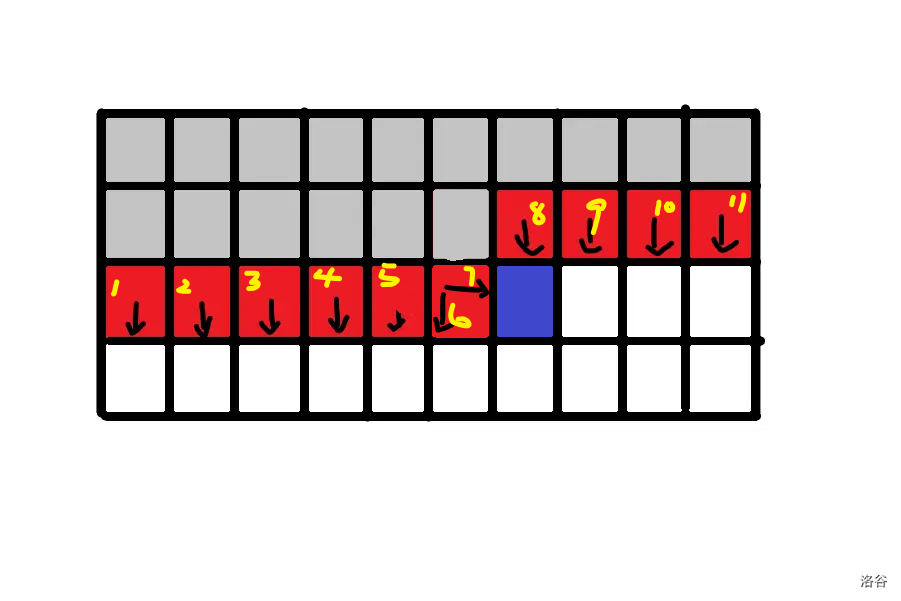
可以看到先前位于 \(j-1\) 格的右插头 \(6\) 变成了下插头，位于 \(j\) 格的下插头 \(7\) 变成了新状态的右插头。转移的时候就要用到这种插头变化规律来直接用存好的进制数操作状态。

现在分讨如何转移。

显然对于本题来讲，右插头和下插头同时出现的情况是不合法的（相当于左侧和上侧的骨牌叠加了），只有出现单个或者一个不出现的情况。

先讨论一个都没出现的情况，因为格子肯定是要放满的所以这个格子一定是一个骨牌的起点，可以考虑放置一个右插头或者下插头，相当于 \(dp_{i,j,S}\rightarrow dp_{i,j,modify(S)}\)。

如果只有右插头相当于这个格子是用来补全那个插头的，新的状态就要把原先状态的右插头扣掉。

如果只有上插头情况是一样的。

每一行转移完后右插头就会归零，此时上次转移的所有状态左移一位才是当前层对应的用于转移的状态，可以想一想。

这种放骨牌的问题普遍比较简单。

白金元首与莫斯科

这个题就是说去放骨牌，然后有障碍，而且没障碍的点可以不放。

先考虑说假如只有障碍这道题怎么做。还是和例子一样的分讨。

如果当前格子是一个障碍，则它不应该出现右插头或者上插头。此时状态 \(S\) 和新状态一致。

if(!a[i][j]){if(!p1&&!p2)Add(f[i][j][S],val);}

接下来讨论格子不为障碍的情况。

如果当前格子不存在右插头或下插头，则有：放置右插头或下插头，或不放置三种方案。不放置则状态不变。

如果要放置一个右插头，回顾上面给的图，放置之后进入下个状态时那个右插头编号应恰好为 \(j+1\)，所以新状态 \(s=S+pw_j\)。

如果要放置下插头则根据图，新状态中下插头编号为 \(j\)，\(s=S+pw_{j-1}\)。进而得到代码。

				else if(!p1&&!p2){
					Add(f[i][j][S],val);
					if(a[i][j+1]){
						int s=S+pw[j];
						Add(f[i][j][s],val);
					}
					if(a[i+1][j]){
						int s=S+pw[j-1];
						Add(f[i][j][s],val);
					}
				}

如果现在只有上插头，则操作之后上插头消去，可以列表分析前后插头的存在情况（因为之后的题插头操作还挺复杂的）。

j-1 j
S 0 1
s 0 0

进而只需减去 \(pw_j\) 编号插头即可转移。

只有右插头的情况是同理的。

				else if(!p1&&p2){
					int s=S-pw[j];	
					Add(f[i][j][s],val);
				}
				else if(p1&&!p2){
					int s=S-pw[j-1];
					Add(f[i][j][s],val);
				}

那就有一个不要脑子的做法就是 \(O(nm)\) 枚举军队所在位置然后跑那么多次dp，那肯定是死了。

考虑优化这个过程，假设现在转移到了军队的格子，则答案应由轮廓线以上和轮廓线以下两部分答案 \(f_{s1},g_{s2}\) 组成，由计数原理对答案的贡献是乘积的形式。然而 \(s1,s2\) 能配对的充要条件是 \(s1\) 的每个轮廓处下插头与 \(s2\) 一一对应。

进而先正常dp出 \(f_{i,j,S}\)，然后反向地 dp出一个对应于 \(f\) 状态的补集答案 \(g_{i,j,s}\)，注意此时插头也应该是一一对应的，然后就会比较绕，得自己画图理解。

最终的对于一个 \(i,j\) 所有的合法状态 \(\{S\}\) 应当是扣去 \(j\) 和 \(j-1\) 两位的全 1 序列的所有子集。放一下代码。

#include<bits/stdc++.h>
#define MAXN 19
#define N (1<<18)+5
#define ll long long
using namespace std;
const int mod=1e9+7;
int n,m,a[MAXN][MAXN];
int f[MAXN][MAXN][N],g[MAXN][MAXN][N];
int pw[MAXN];
inline void Add(int &x,int y){
	x=x+y>mod?x+y-mod:x+y;
}
int ans[MAXN][MAXN];
signed main(){
	pw[0]=1;
	for(int i=1;i<MAXN;i++)pw[i]=pw[i-1]<<1;
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]),a[i][j]^=1;
	int toT=(1<<(m+1))-1;
	f[0][m][0]=1;//正着dp
	for(int i=1;i<=n;i++){
		for(int j=0;j<=toT;j++)f[i][0][j<<1]=f[i-1][m][j];
		for(int j=1;j<=m;j++){
			for(int S=0;S<=toT;S++){
				int p1=(S>>(j-1))&1,p2=(S>>(j))&1,val=f[i][j-1][S];
				if(!val)continue;
				if(!a[i][j]){if(!p1&&!p2)Add(f[i][j][S],val);}
				else if(!p1&&!p2){
					Add(f[i][j][S],val);
					if(a[i][j+1]){
						int s=S+pw[j];
						Add(f[i][j][s],val);
					}
					if(a[i+1][j]){
						int s=S+pw[j-1];
						Add(f[i][j][s],val);
					}
				}
				else if(!p1&&p2){
					int s=S-pw[j];	
					Add(f[i][j][s],val);
				}
				else if(p1&&!p2){
					int s=S-pw[j-1];
					Add(f[i][j][s],val);
				}
			}
		}
	}
	g[n+1][1][0]=1;//倒着dp，这块真挺绕的。
//因为转移方向完全相反并且转移状态又是基于正着的状态配对的，所以乍一看会觉得状态转移很怪，得画图仔细想。
	for(int i=n;i>=1;i--){
		for(int j=0;j<=toT;j++)Add(g[i][m+1][j>>1],g[i+1][1][j]);
		for(int j=m;j>=1;j--){
			for(int S=0;S<=toT;S++){
				int p1=(S>>(j-1))&1,p2=(S>>j)&1,val=g[i][j+1][S];
				if(!val)continue;
				if(!a[i][j]){if(!p1&&!p2)Add(g[i][j][S],val);}
				else if(!p1&&!p2){
					Add(g[i][j][S],val);
					if(a[i][j-1]){
						int s=S+pw[j-1];
						Add(g[i][j][s],val);
					}
					if(a[i-1][j]){
						int s=S+pw[j];
						Add(g[i][j][s],val);
					}
				}
				else if(!p1&&p2){
					int s=S-pw[j];
					Add(g[i][j][s],val);
				}
				else if(p1&&!p2){
					int s=S-pw[j-1];
					Add(g[i][j][s],val);
				//	printf("g %lld %lld %lld=%lld\n",i,j,s,g[i][j][s]);
				}
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(!a[i][j])continue;
			int S=toT^pw[j-1]^pw[j];
			for(int s=S;s;s=(s-1)&S)Add(ans[i][j],(ll)f[i][j-1][s]*g[i][j+1][s]%mod);
			Add(ans[i][j],(ll)f[i][j-1][0]*g[i][j+1][0]%mod);
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++)printf("%d ",ans[i][j]);
		printf("\n");
	}
	return 0;
}

一条回路与多条回路问题

Eat the Trees

这块才开始正经插头dp，分讨就会开始复杂。

仍然讨论当前格相邻的右插头和上插头。

当前格为障碍时：只有右上插头都不存在才能转移

不为障碍时：

右上插头都不存在时：

由于本题要求全部被覆盖，则此时必须新建一个回路即连通分量，在状态上，相当于同时新建了两个插头。

				else if(!p1&&!p2){	
					int s=S+pw[j]+pw[j-1];
					dp[now][j][s]+=val;
				}

只存在右插头时：

这个时候相当于延续右插头的路径，且上插头不存在，所以可以选择向右或向下走。这个时候就要列表了：

想往右走，先前的右插头对应 \(j-1\)，放置后右插头对应 \(j\) 且右插头所在格没有下插头。

j-1 j
S 1 0
s 0 1

也就是说当减去 \(j-1\) 插头并加上 \(j\) 插头才能由 \(S\) 变为 \(s\)。

想往下走，先前的右插头对应 \(j-1\)，放置后下插头对应 \(j-1\) 且右插头所在格没有右插头（什。不难发现此时状态是不变的。

另外，能走向那个方向的前提是那个点不是障碍点。

				else if(p1&&!p2){
					if(a[i+1][j]){
						int s=S;
						dp[now][j][s]+=val;
					}
					if(a[i][j+1]){
						int s=S-pw[j-1]+pw[j];
						dp[now][j][s]+=val;
					}
				}

只存在下插头的推导留给自己当习题活动大脑真的不是懒得码字吗，只放代码。

				else if(!p1&&p2){
					if(a[i+1][j]){
						int s=S-pw[j]+pw[j-1];
						dp[now][j][s]+=val;
					}
					if(a[i][j+1]){
						int s=S;
						dp[now][j][s]+=val;
					}
				}

两个插头同时存在。

这道题中这种情况时合法且必须要存在的，因为我们是在从上往下从左往右dp，所以这种情况等效于闭合了当前回路的一部分。闭合后两个插头全部抵消，减去即可。

				else if(p1&&p2){
					int s=S-pw[j]-pw[j-1];
					dp[now][j][s]+=val;
				}

没有找到其他的题...

一条回路

【模板】插头 DP

一条回路总要比多条回路简单的...吗？

实则不然，因为要保证最终只存在一个联通块，所以在上文分讨的基础上，两个插头都存在的时候就不能无脑合并了。板子放在这个位置是有原因的

引理：对于穿过轮廓线的从左到右的四个不一定连续的插头 \(a,b,c,d\)，若 \(ac\) 联通则 \(bd\) 一定不联通。 要不然路径就重了。

既然如此，对于当前轮廓线上的若干插头，一个已确定的合法方案大概长成这样：

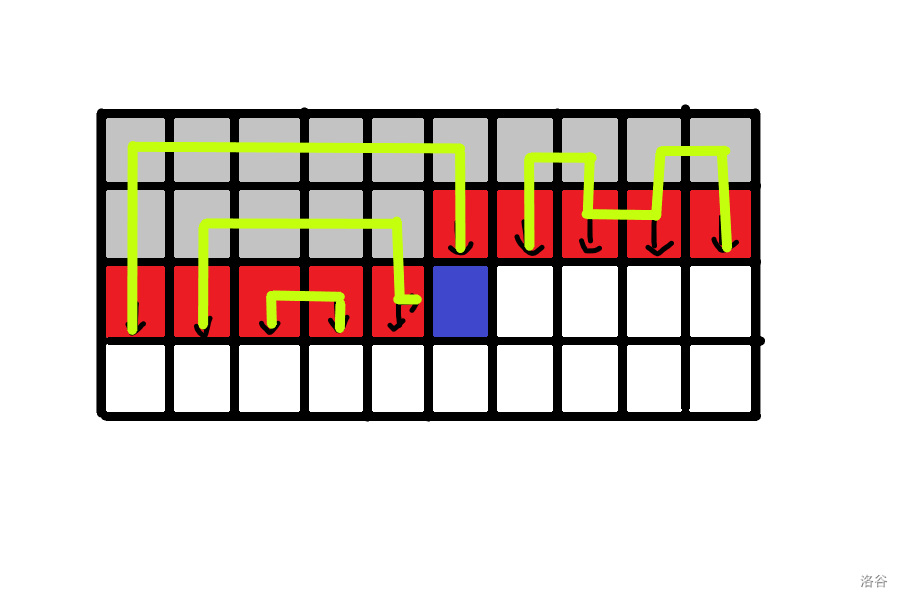
发现这样的关系很像一个括号序列，进而地，将已确定的插头分为左括号和右括号。dp的过程就是一个建立并最终完成合并括号序列的过程。

然后看括号序列如何维护出一条回路。

显然除了两个插头都存在的情况，其他情况的处理可以直接照搬上一题。

将插头的二进制表示改为四进制，012分别表示没有插头，左括号和右括号，现在讨论当前格子右插头和下插头 \(p1,p2\) 的状态。

\(p1=p2=1\)

相当于是两个左括号，此时可以把两个左括号拼接到一起（直接删），这之后内层括号序列的右括号会失效转而成为外层括号序列的左括号。找内层右括号可以用模拟栈暴力实现。找到之后进行一个删右加左的操作。

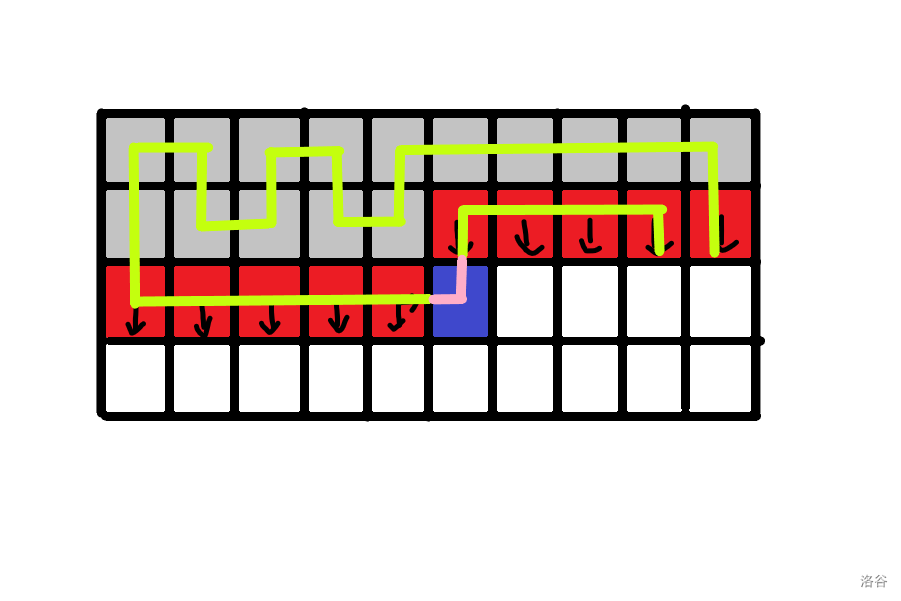
\(p1=p2=2\)

相当于两个右括号，合并然后向左找内层左括号同理。

\(p1=2,p2=1\)

这会相当于把两个括号序列拼起来了，然后捏掉中间的两个括号。

\(p1=1,p2=2\)

根据转移的特点，这样的操作一定是一次回路的闭合，但是肯定不能想闭合就闭合，毕竟点是要走遍的。所以找到转移中最后的合法点，当且仅当在该点时能对答案做出贡献。

关于实现

四进制对空间的消耗相当大，考虑用hashtable映射掉这些状态。具体看代码。

#include<bits/stdc++.h>
#define int long long
#define MAXN 15
#define N 300005
#define L(i) (pw[i])
#define R(i) (2*pw[i])
#define At(x,i) ((x)*pw[i])
int n,m;
char txt[MAXN];
int a[MAXN][MAXN],ex,ey;
int pw[MAXN];
int now,dp[2][N],sta[2][N],tot[2];
int ans;
struct Hash_Table{
	int h[N],nxt[N];
	const int mod=299989;
	inline void add(int x,int val){
		int u=x%mod+1;
		for(int i=h[u];i;i=nxt[i]){
			int v=sta[now][i];
			if(x==v){
				dp[now][i]+=val;
				return ;
			}
		}
		nxt[++tot[now]]=h[u],h[u]=tot[now];
		sta[now][tot[now]]=x,dp[now][tot[now]]=val;
	}
	inline void  reset(){memset(h,0,sizeof(h)),tot[now]=0;}
}H;
signed main(){
	pw[0]=1;
	for(int i=1;i<=12;i++)pw[i]=pw[i-1]<<2;
	scanf("%lld%lld",&n,&m);
	for(int i=1;i<=n;i++){
		scanf("%s",txt+1);
		for(int j=1;j<=m;j++){
			a[i][j]=txt[j]=='.';
			if(a[i][j])ex=i,ey=j;
		}
	}
	tot[now]=dp[now][1]=1,sta[now][1]=0;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=tot[now];j++)sta[now][j]<<=2;
		for(int j=1;j<=m;j++){
			int lst=now;
			now^=1;
			H.reset();
			for(int k=1;k<=tot[lst];k++){
				int S=sta[lst][k];
				int p1=(S>>((j-1)*2))%4,p2=(S>>(j*2))%4,val=dp[lst][k];
				if(!a[i][j]){//有障碍 
					if(!p1&&!p2)H.add(S,val);
				}
				else if(!p1&&!p2){//新联通块 
					if(a[i+1][j]&&a[i][j+1]){
						int s=S+L(j-1)+R(j);
						H.add(s,val);
					}
				}
				else if(!p1&&p2){//下/右 
					if(a[i][j+1]){
					/*
					右，向右的插头是会换的
					原本在j-1是.,j是下，向右之后就是j处有右插头，和原先j处有上插头是一样表示的 
					*/
						int s=S;
						H.add(s,val);
					}
					if(a[i+1][j]){
					//下的话j的右插头就没了，但是这一格子有下插头(对应到j-1位)。
						int s=S-At(p2,j)+At(p2,j-1);
						H.add(s,val);	
					}
				}
				else if(p1&&!p2){//转移方向是一致的 
					if(a[i][j+1]){//现在向右的话原本j有右插头现在没了，然后多了j-1(当前格)的下插头 
						int s=S+At(p1,j)-At(p1,j-1);
						H.add(s,val);
					}
					if(a[i+1][j]){//这时候右插头变成现在的下插头了，表示不变,往下走了右插头就没了，但是p2本身就不存在，所以仍不变。
						int s=S;
						H.add(s,val); 
					}
				}
				else if(p1==1&&p2==1){
					/*
					两个左括号，半个回形，合并，合并完这俩左括号都没了。 
					但是这样的话p2的左括号对应的右括号就不是右括号而是左括号了，p1仍可以和p2或者别的配对所以还是右括号 
					*/
					int cnt=1;
					for(int l=j+1;l<=m;l++){
						if((S>>(2*l))%4==1)++cnt;
						if((S>>(2*l))%4==2)--cnt;
						if(!cnt){
							int s=S-L(j-1)-L(j)-R(l)+L(l);
							H.add(s,val);
							break;
						}
					}
				}
				else if(p1==2&&p2==2){
					/*
					两个右括号，还是合并，然后p1左括号失效变成右括号。 
					*/
					int cnt=-1;
					for(int l=j-2;l>=0;l--){
						if((S>>(2*l))%4==1)++cnt;
						if((S>>(2*l))%4==2)--cnt;
						if(!cnt){
							int s=S-R(j-1)-R(j)-L(l)+R(l);
							H.add(s,val);
							break;
						}
					} 
				}
				else if(p1==2&&p2==1){
					/*
					左边右括号右边左括号就直接合并，两个括号序列捏成一个了。 
					*/
					int s=S-R(j-1)-L(j);
					H.add(s,val);
				}
				else if(i==ex&&j==ey)ans+=val;
			}
		}
	}
	printf("%lld\n",ans);
	return 0;
}

双倍经验

bzoj3125

考虑一下 - 和 | 的路径怎么处理，其他的就是板子。

对于 - 相当于所有下插头的目标点既不能是障碍点也不能是 -，转移的时候只能考虑右插头的情况。对于 | 是类似的，板子改一改就能过。

神奇游乐园

插头dp也可以用来解决最优化问题。具体地，设 \(dp_{i,j,S}\) 表示到格点 \((i,j)\) 状态为 \(S\) 时的最优方案，注意只要是延伸插头，当前格点都是必选的（因为有插头相当于先前钦定了必须走...），除非是新建联通分量的时候可以不选。

正在施工。

标签：插头,p2,p1,pw,val,记录,int,DP
From： https://www.cnblogs.com/Claimo0611/p/18673649

相关文章

  • 数据结构学习记录-数据结构概念
    1数据结构：数据结构是计算机存储，管理数据的方式。数据必须依据某种逻辑联系组织在一起存储在计算机内数据结构研究的就是这种数据的存储结构和数据的逻辑结构。1.1数据的逻辑结构：逻辑结构指的是数据本身之间的关系集合：数据元素除了属于同一个集合外，没有其他联系；线性关......
  • Windows的小问题记录-更新到win11后录屏无法录制麦克风的声音（已解决）
    问题描述：录屏无法录进麦克风的声音。背景详情：平时不用耳机（有线还是无线都不用），所以不是“忘记开耳机权限”“忘记把耳机上的麦克风按钮打开”“把耳机的线插错口”之类的问题；检查过录屏软件的麦克风权限（图3）、火绒隐私设备保护里的麦克风保护（图4）、Xbox游戏录屏设置里关于音频麦克风......
  • 字符串dp+匹配
    https://codeforces.com/problemset/problem/2050/E#include<bits/stdc++.h>usingnamespacestd;#defineendl'\n'usingll=longlong;usingpii=pair<char,int>;constdoublePI=acos(-1);constintN=1e3+10;constintmod=1e9......
  • STM32F1基于HAL库的学习记录实用使用教程分享(四、OLED IIC)
    往期内容STM32F1基于HAL库的学习记录实用使用教程分享(一、GPIO_Output)STM32F1基于HAL库的学习记录实用使用教程分享(二、GPIO_Input按键)STM32F1基于HAL库的学习记录实用使用教程分享(三、外部中断按键)文章目录往期内容前言一、IIC1.概念2.IIC作用3.IIC的特点II......
  • 关于Ubuntu安装Mujoco的记录
    前言这篇博客主要用于记录一些关于mujoco如何安装、urdf模型如何导入以及如何进行仿真的记录的事情，特此记录，一方面便于日后自己的温故学习，另一方面也比便于大家的学习和交流。如有不对之处，欢迎评论区指出错误，你我共同进步学习！正文让我们安装mujoco1、安装----安装mojoco----......
  • 线程每次iodelay监控及D状态开始和结束监控并做堆栈记录
    一、背景在之前的博客 获取进程或线程级别的iodelay的方法_io验证延时链-CSDN博客里，我们讲到了获取进程或线程的iodelay的方法，但是博客里讲到的获取iodelay的值是一个累积值，并不能准确的捕获到每个单次的iodelay具体是多少。这篇博客里是为了监控每个单次的iodelay，除了监控i......
  • 如何在电脑桌面上记录每日工作任务清单并准时提醒？
    每天的工作任务很多，而且需要在截止时间就完成，如何能够简单、高效管理每日工作任务呢？我的建议是直接在电脑桌面上记录每日工作任务清单，并设置提醒时间，到期后收到提醒就不会忘记了！接下来给大家介绍2款极简但好用的电脑桌面待办清单APP！一、Win系统自带的日历在Windows电脑上，点击......
  • Sigrity System SI SerialLink模式进行USB3.1协议仿真分析操作指导-SuperSpeedPlus_Rx
    SigritySystemSISerialLink模式进行USB3.1协议仿真分析操作指导-SuperSpeedPlus_Rx_HostSigritySystemSISerialLink模式提供了10个协议合规性检查工具模板，用户可以将根据实际应用替换模板中的SPICE文件，然后进行协议仿真分析，同时软件还提供了目标结果的模板MASK以及该协......
  • 【02】做一个精美的打飞机小游戏，python开发小游戏-鹰击长空—优雅草央千澈-持续更新-
    【02】做一个精美的打飞机小游戏，python开发小游戏-鹰击长空—优雅草央千澈-持续更新-分享源代码和游戏包供游玩-记录完整开发过程-用做好的素材来完善鹰击长空1.0.1版本背景之前优雅草央千澈在AE特效制作处博文已经完整介绍了本款游戏的素材开发，本文开始把素材利用起来放进去......
  • 如何解决云服务器上UDP端口无法开放的问题？
    关于云服务器上UDP端口无法开放的问题，通常涉及多个方面的原因，包括安全组设置、防火墙规则、操作系统配置等。以下是详细的排查和解决方案：检查安全组设置：云服务器的安全组是控制网络流量进出的重要机制。如果安全组规则没有正确配置，UDP端口将无法开放。请按照以下步骤检查并调......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99