题解：AT_abc353_f [ABC353F] Tile Distance

[ABC353F] Tile Distance 题解

cnblogs

题目传送门：洛谷，Atcoder

Solution

很恶心人的分类讨论题。

很显然走大格子大概率比走小格子快。

对终点和起点向上下左右枚举大格子，我们就把问题转化为给两个大格子 \((a,b)\)、\((c,d)\)，求怎样走最快。

对角的大格子可以通过 \(2\) 步相互到达，如下图所示。

于是我们可以以以下路径，这是一般情况的最短路径，步数为 \(\max(|a-c|,|b-d|)\)。（据说这是切比雪夫距离）

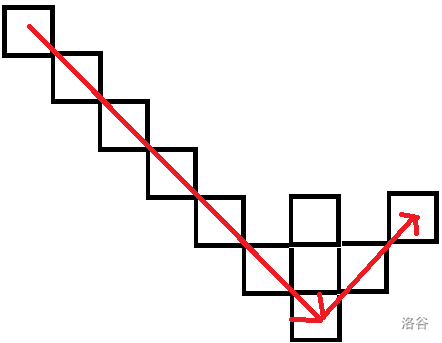
然而当 \(k \leq 2\)，最后一段路不需要上下横跳，直接横穿小格子即可，步数为 \(\frac{k+1}{2}\min(|a-c|,|b-d|)+||a-c|-|b-d||\)。

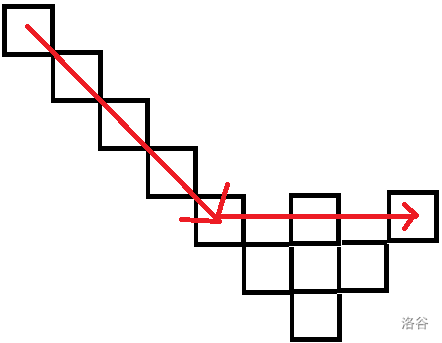
最后要讨论只通过小格子达到的情况，就让上面算出的答案和曼哈顿距离去最小值就好了。

注意：若起点和终点在同一个小格子的块中，答案不一定是他们的曼哈顿距离，就像下图所示的情况，显然红线比绿线短。

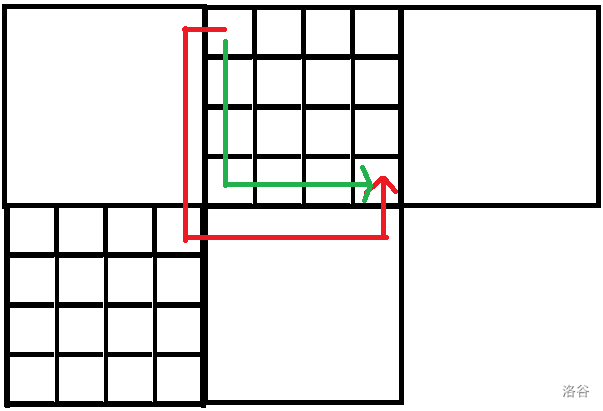
code

#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
#include<queue>
#include<cstring>
#include<cmath>
#include<cassert>
#define pr pair < long long, pair<long long, long long> >
#define mp make_pair
using namespace std;
long long k, sx, sy, tx, ty;
long long gt(long long ax, long long ay, long long bx, long long by){
	long long a = abs(ax - bx), b = abs(ay - by), ans = max(a, b) * 2, sp = max(a, b) - min(a, b);
	if(k == 1)
		return a + b;
	if(k == 2)
		return a + b + sp / 2;
	return ans;
}
vector < pr > a, b;
int main(){
	cin >> k >> sx >> sy >> tx >> ty;
	long long dsx = sx / k, dsy = sy / k, dtx = tx / k, dty = ty / k;
	long long dis = max(sx, tx) - min(sx, tx) + max(sy, ty) - min(sy, ty);
	if((dsx + dsy) % 2 == 0){
		a.push_back(mp(sx - dsx * k + 1, mp(dsx - 1, dsy)));
		a.push_back(mp(sy - dsy * k + 1, mp(dsx, dsy - 1)));
		a.push_back(mp((dsx + 1) * k - sx, mp(dsx + 1, dsy)));
		a.push_back(mp((dsy + 1) * k - sy, mp(dsx, dsy + 1)));
	}
	else
		a.push_back(mp(0, mp(dsx, dsy)));
	if((dtx + dty) % 2 == 0){
		b.push_back(mp(tx - dtx * k + 1, mp(dtx - 1, dty)));
		b.push_back(mp(ty - dty * k + 1, mp(dtx, dty - 1)));
		b.push_back(mp((dtx + 1) * k - tx, mp(dtx + 1, dty)));
		b.push_back(mp((dty + 1) * k - ty, mp(dtx, dty + 1)));
	}
	else
		b.push_back(mp(0, mp(dtx, dty)));
	long long minn = dis;
	for(auto i : a)
		for(auto j : b)
			minn = min(minn, i.first + j.first + gt(i.second.first, i.second.second, j.second.first, j.second.second));
	cout << minn << endl;
	return 0;
}