[ARC138E] Decreasing Subsequence
题意
给出 \(3\leq n \leq 5000,2\leq k \leq (n+1)/2\),对所有长度为 \(n\) 的满足 \(0\leq a_i \leq i\) 且正数项两两不同的序列 \(a\),求长度为 \(k\) 的元素非 \(0\) 的下降子序列个数之和。
思路
先刻画序列。
对所有 \(a_i\) 减去 \(1\),新的序列是 \(a'\)。
对于所有 \(a_i'\neq -1\),必须有 \(a_i'<i\)。连接一条 \(i \to a_i'\) 的边,满足这条边必须方向向前。而且由于所有非负整数互不相同,建出来的图必须是若干条不相交的链。
比如下面酱子,就是一个合法的 \(a'\) 了。
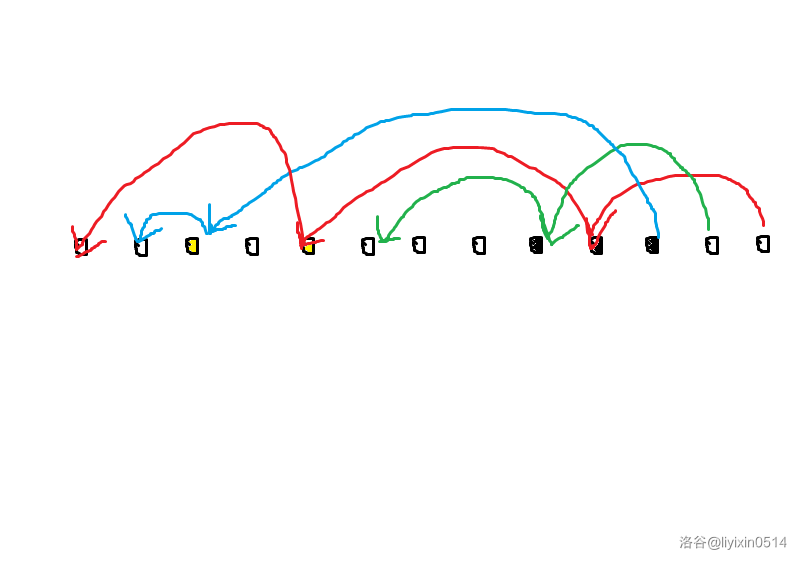
接下来刻画下降子序列。
下降子序列 \(\{s_i\}\),必须满足这些点有出边,而且它们的出边刚好形成一个像彩虹一样的包含形状。
比如上图中标黄色和标黑色分别就是其中两组合法子序列。
合法的连边方案和合法的序列是双射。我们要对每个合法的连边方案计算有多少长度为 \(k\) 的合法子序列。
子序列的刻画太难拍成状态了,不好算。于是我们转为算每种合法的大小为 \(k\) 的“彩虹”连边有多少合法的连边方式吧。这好啊,还不用考虑算重,因为每种不同的子序列出现在同一个序列里面,你也得分别算贡献的。
对于一组彩虹边,起点有 \(k\) 个,分别是 \(s_1 \sim s_k\),终点也有 \(k\) 个,分别是 \(t_1 \sim t_k\)。计算序列个数。每个 \(s_i\) 可以向后连长度任意的链,每个 \(t_i\) 可以向前连长度任意的链。剩下没有被用到的点,可以随便分成任意条链。
枚举 \(l\) 表示终点和终点连的链的点的个数,\(r\) 表示起点和起点连的链的点的个数。\(n \brace m\) 是第二类斯特林数的意思。
答案是:(\(n+1\) 是因为图里面还有 \(0\) 号点)
\[\sum_{l=k} \sum_{r=k}^{l+r\le n+1} \binom{n+1}{l+r} {l \brace k} {r \brace k} f_{n+1-l-r}\\ f_i = \sum_{x=1}^i {i \brace x} \]解释一下组合意义:上面那条就是在 \(n+1\) 个点里面,选出 \(l+r\) 个点,并且左边分 \(l\) 个,右边分 \(r\) 个,左右都分别分成 \(k\) 条链,每条链上点的顺序和链于链之间的顺序都是按照编号有序的。\(f_i\) 就表示剩下 \(i\) 个点分成任意组链的方案数。
预处理第二类斯特林数,预处理 \(f_i\)。时间复杂度 \(O(n^2)\)。
code
代码好写啊。
#include<bits/stdc++.h>
#define sf scanf
#define pf printf
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
using namespace std;
typedef long long ll;
namespace hesitate {
constexpr int N=5e3+7,Max=5e3+1,mod=1e9+7;
int add(int a,int b) { return a+b>=mod ? a+b-mod : a+b; }
void _add(int &a,int b) { a=add(a,b); }
int mul(int a,int b) { return 1ll*a*b%mod; }
void _mul(int &a,int b) { a=mul(a,b); }
int ksm(int a,int b=mod-2) {
int s=1;
while(b) {
if(b&1) _mul(s,a);
_mul(a,a);
b>>=1;
}
return s;
}
int s[N][N],f[N],fac[N],ifac[N];
int n,k;
void init() {
s[0][0]=1;
rep(i,1,Max) rep(j,1,i) s[i][j]=add(s[i-1][j-1],mul(j,s[i-1][j]));
f[0]=1;
rep(i,1,Max) rep(j,1,i) _add(f[i],s[i][j]);
fac[0]=1;
rep(i,1,Max) fac[i]=mul(fac[i-1],i);
ifac[Max]=ksm(fac[Max]);
per(i,Max-1,0) ifac[i]=mul(ifac[i+1],i+1);
}
int C(int n,int m) { return mul(fac[n],mul(ifac[m],ifac[n-m])); }
int ans;
void main() {
sf("%d%d",&n,&k);
init();
rep(l,k,n+1-k) rep(r,k,n+1-l) {
_add(ans,mul(C(n+1,l+r),mul(mul(s[l][k],s[r][k]),f[n+1-l-r])));
}
pf("%d\n",ans);
}
}
int main() {
#ifdef LOCAL
freopen("in.txt","r",stdin);
freopen("my.out","w",stdout);
#endif
hesitate :: main();
}