注:题解中 \(\operatorname{lsh}\),\(\operatorname{rsh}\),\(\operatorname{or}\) 分别表示按位左移、按位右移、按位或,即 c++ 语言中的 <<,>>,|。
我也是打上轮廓线 DP 了。
设 \(f_{x,y,S}\) 表示当前在 \((x,y)\) 格子,前 \(m\) 个格子的状态为 \(S\) 时的最小花费。
这里的状态是指,这一格竖着覆盖为 \(1\),横着覆盖或本来就不用覆盖为 \(0\)。
这里的前 \(m\) 个格子如下图所示,假设 \(m=4\),当前在 \((2,2)\),方格内的数表示在 \(S\) 中从低到高的下标(从 \(0\) 开始):
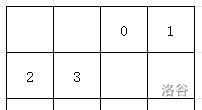
它就是一个逐行遍历矩阵的顺序,注意是包括 \((x,y)\) 这一格的。
为什么要这样记录呢,因为存在竖着覆盖,如刚才的例子,\((2,2)\) 的下一个为 \((2,3)\),它的上面是 \((1,3)\),刚好被记录了状态。
于是转移其实不难想:
- 下一位 \((nx,ny)\) 为
#- 横着覆盖,判断左边有没有点,且这个点是不是横着覆盖的,即 \(f_{nx,ny,S\operatorname{rsh}1}\) 从 \(f_{x,y,S}\) 或 \(f_{x,y,S}+1\) 转移。
- 竖着覆盖,判断上面的点是不是竖着覆盖的,即 \(f_{nx,ny,(S\operatorname{rsh}1)\operatorname{or}(1\operatorname{lsh}(m-1))}\) 从 \(f_{x,y,S}\) 或 \(f_{x,y,S}+1\) 转移。
- 下一位为
.,直接让 \(f_{nx,ny,S\operatorname{rsh}1}\) 从 \(f_{x,y,S}\) 转移。
复杂度 \(O(nm2^m)\)。
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define read(x){\
char ch;\
int fu=1;\
while(!isdigit(ch=getchar()))\
fu-=(ch=='-')<<1;\
x=ch&15;\
while(isdigit(ch=getchar()))\
x=(x<<1)+(x<<3)+(ch&15);\
x*=fu;\
}
using namespace std;
namespace asbt{
namespace cplx{bool begin;}
const int maxn=(1<<10)+5;
const int inf=0x3f3f3f3f;
int n,m,f[maxn][15][maxn];
char s[maxn][15];
il void upd(int &x,int y){
x=min(x,y);
}
namespace cplx{
bool end;
il double usdmem(){return (&begin-&end)/1048576.0;}
}
int main(){
read(n)read(m);
for(int i=1;i<=n;i++){
scanf(" %s",s[i]+1);
}
memset(f,0x3f,sizeof f);
if(s[1][1]=='#'){
f[1][1][0]=f[1][1][1<<(m-1)]=1;
}
else{
f[1][1][0]=0;
}
for(int x=1;x<=n;x++){
for(int y=1;y<=m;y++){
for(int S=0,nx,ny;S<1<<m;S++){
if(f[x][y][S]>=inf){
continue;
}
nx=x+y/m;
ny=y%m+1;
if(s[nx][ny]=='#'){
if(ny>1&&(S>>(m-1)&1)==0&&s[x][y]=='#'){
upd(f[nx][ny][S>>1],f[x][y][S]);
}
else{
upd(f[nx][ny][S>>1],f[x][y][S]+1);
}
if(nx>1&&(S&1)){
upd(f[nx][ny][S>>1|1<<(m-1)],f[x][y][S]);
}
else{
upd(f[nx][ny][S>>1|1<<(m-1)],f[x][y][S]+1);
}
}
else{
upd(f[nx][ny][S>>1],f[x][y][S]);
}
}
}
}
int ans=inf;
for(int S=0;S<1<<m;S++){
ans=min(ans,f[n][m][S]);
}
printf("%d",ans);
return 0;
}
}
int main(){return asbt::main();}