Paper-cutting:思维很好,但代码很构式的 manacher 题。
蒟蒻 2025 年切的第一道题,是个紫,并且基本独立想出的,特此纪念。
判断能否折叠
我们先考虑一部分能折叠需要满足什么条件。显然,这一部分需要是一个长度为偶数的回文串。
那么横向和纵向会不会影响呢?答案是不会,因为横向折了之后,折过去的部分一定是对称的,那么只要原来某两列相等,这之后这两列还是相等的。我们可以画图理解:
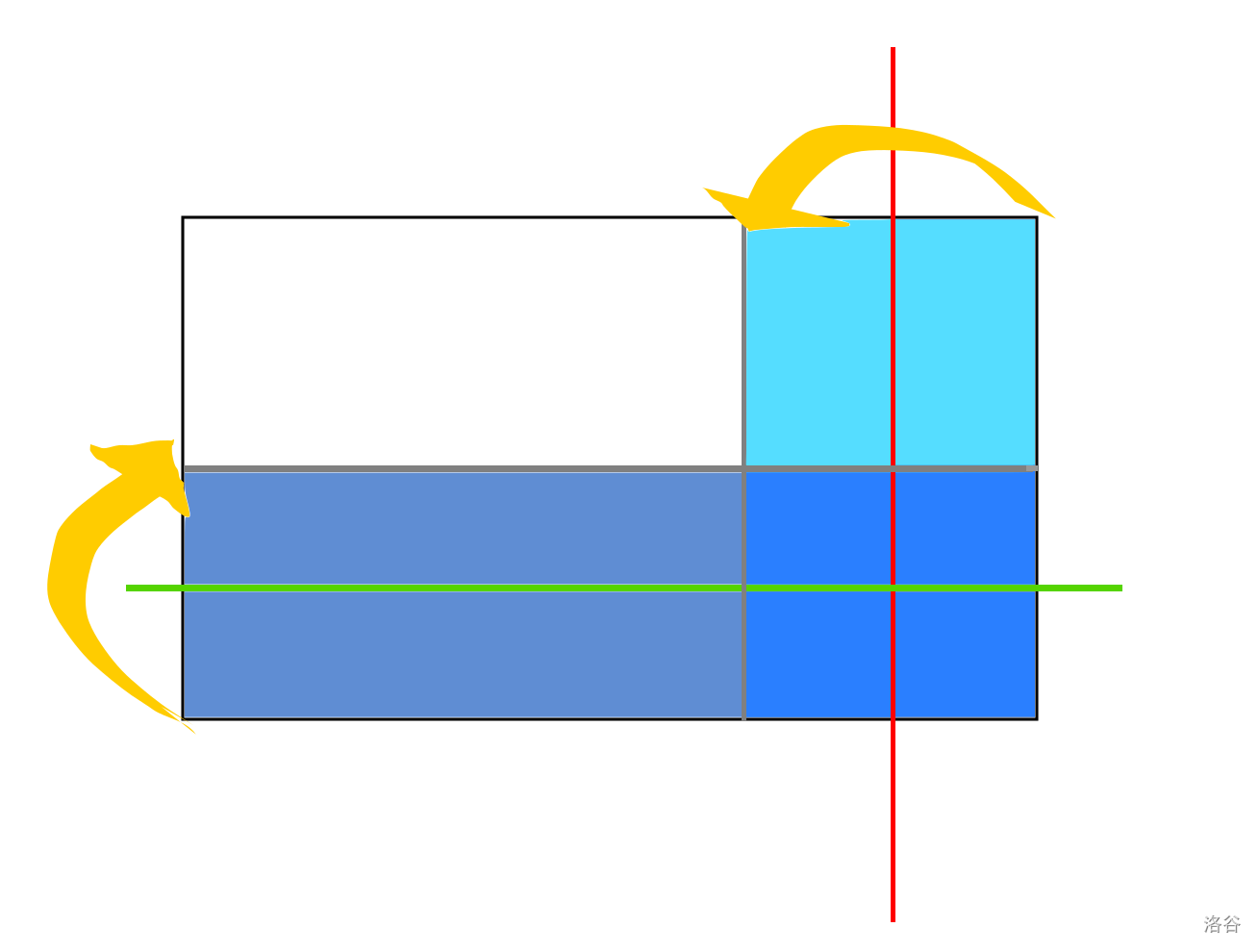
相同颜色的部分代表这两部分相等。
于是,我们只需要对每行每列哈希一遍,然后利用偶数回文串折叠即可。同时我们也得出横行和纵列互不影响的结论。
这一部分可以用 manacher 快速求出最大折叠半径。
折叠策略
我们先考虑这个问题的弱化版。
只能折一边时
在只能折一边时,我们一定会尽可能地折叠。这样一定更优。
证明也是容易的,折叠前折叠部分单独的连通块会被砍掉,与剩余部分相连接的连通块因为是对称过去,所以折叠过去后一定存在一个格子使它们依然连通。
因此,折叠后连通块的个数一定不会增加,答案也一定不劣。同时,折叠的顺序也是无影响的,因为每次能折叠当且仅当偶数回文串内存在一个能折叠到的点。
两边都能折时
同样是能折就折,因为左折、右折互不影响,我们可以用分类讨论来证明。
右折后左折能正常进行时
显然左右都能操作。
右折后左折被挡住一部分时
这种情况一定不存在。
左折要被挡住,必然要满足下图:
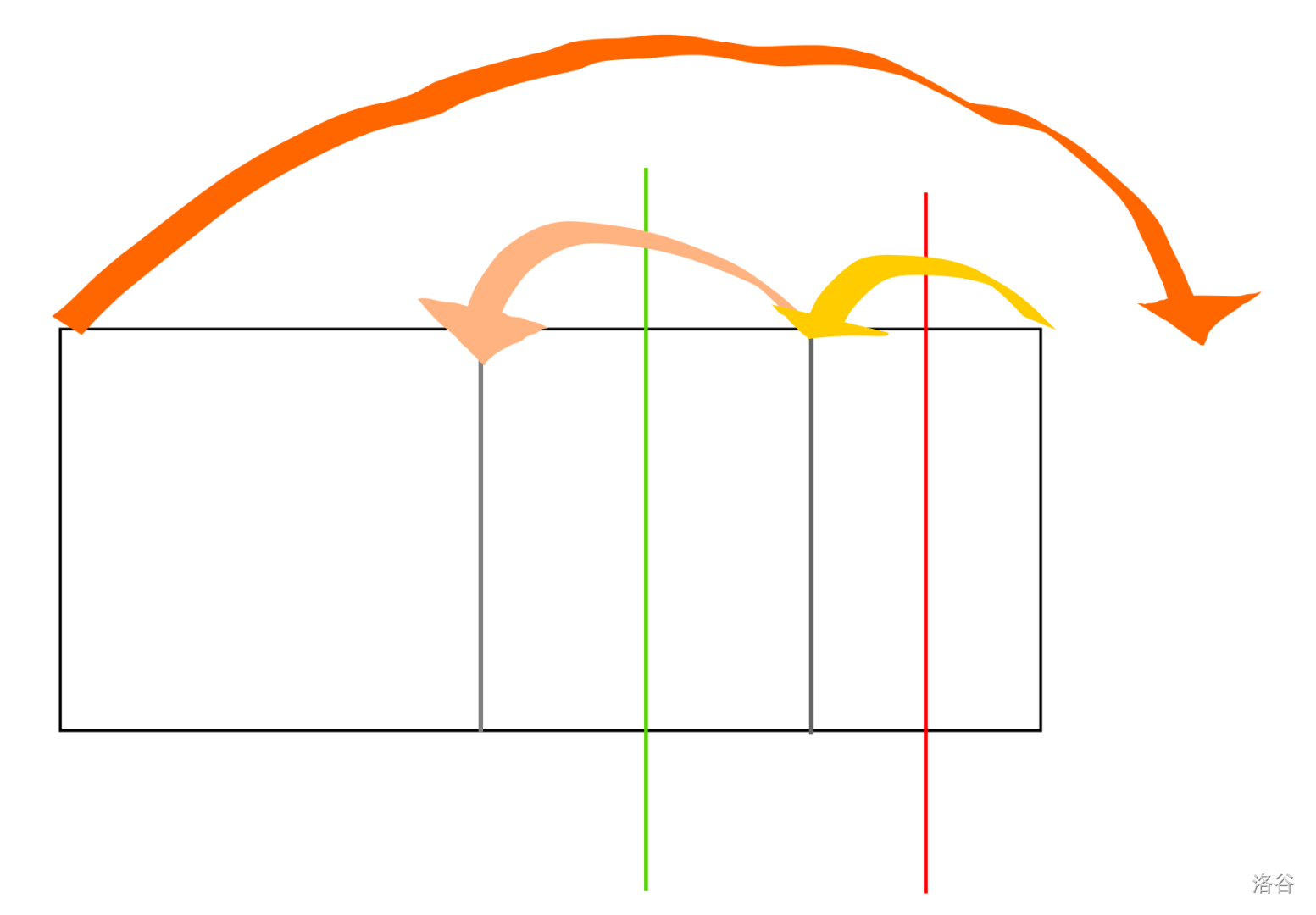
而橙色的左折显然不合法,这种情况等效于浅橙色部分右折。
因此能折就折的策略一定不劣。
翻折实现
对每行每列跑 manacher 记录最长回文长度后,我们考虑设计 dp。
以向左翻折为例,定义 \(dp_i\) 表示以 \(i\) 为最后一列是否可行,\(d_i\) 为回文半径长度,则:
\[dp_i=[(\sum_{j=i+1}^{i+d_i}dp_j) >0] \]这个式子可以用前缀和优化、单调队列优化来做,或者跟我一样维护一个最近的 \(1\) 的指针也可以。
注意初始化 \(dp_n=1\)。
向左翻折后,从左边开始再往右翻折一遍就可以了。注意不能翻过新的右边界。
最后求出左右边界、上下边界后,进行 BFS 求出需要减掉的连通块个数即可。
时间复杂度 \(O(nm)\),注意动态开数组。
代码
非常构式,调了 2h。
#include <bits/stdc++.h>
#define fi first
#define se second
#define lc (p<<1)
#define rc ((p<<1)|1)
#define eb(x) emplace_back(x)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
using pi=pair<int,int>;
const ull nosol1=1145141919810,nosol2=1919810114514,nosol3=1911451419810;
int n,m,x,ansxl,ansxr,ansyl,ansyr,d[2000005];
int gox[]={0,0,1,-1};
int goy[]={-1,1,0,0};
vector<int>c[1000005];
ull xhs[1000005],yhs[1000005],f[2000005];
void init(int len,ull *arr)
{
x=0;
f[0]=nosol1;
f[++x]=nosol2;
for(int i=1;i<=len;i++)f[++x]=arr[i],f[++x]=nosol2;
f[x+1]=nosol3;
}
void manacher()
{
for(int i=1;i<=x;i++)d[i]=0;
d[1]=1;
for(int i=2,l=0,r=0;i<=x;i++)
{
if(i<=r)d[i]=min(r-i+1,d[l+r-i]);
while(f[i-d[i]]==f[i+d[i]])d[i]++;
if(i+d[i]-1>r)l=i-d[i]+1,r=i+d[i]-1;
}
}
void do_dp(int len,int &ansl,int &ansr)
{
ansr=len;
for(int i=len-1;i>=1;i--)
{
int p=i*2+1;
int dx=d[p]/2;
if(i+dx>=ansr)ansr=i;
}
ansl=1;
for(int i=1;i<ansr;i++)
{
int p=i*2+1;
int dx=d[p]/2;
if(i-dx+1<=ansl)ansl=i+1;
}
}
bool legal(int x,int y){return (x>=ansxl&&x<=ansxr&&y>=ansyl&&y<=ansyr);}
void bfs(int x,int y)
{
queue<pi>q;
q.push({x,y});
c[x][y]=1;
while(!q.empty())
{
pi u=q.front();
q.pop();
int nx=u.fi,ny=u.se;
for(int i=0;i<4;i++)
{
int tx=nx+gox[i],ty=ny+goy[i];
if(legal(tx,ty)&&c[tx][ty]==0)
{
q.push({tx,ty});
c[tx][ty]=1;
}
}
}
}
void solve()
{
int ans=0;
cin>>n>>m;
for(int i=1;i<=n;i++)c[i].clear();
for(int i=1;i<=n;i++)xhs[i]=0;
for(int i=1;i<=m;i++)yhs[i]=0;
for(int i=1;i<=n;i++)
{
c[i].eb(0);
for(int j=1;j<=m;j++)
{
char tmp;
cin>>tmp;
int k=tmp-'0';
xhs[i]=xhs[i]*2+k;
yhs[j]=yhs[j]*2+k;
c[i].eb(k);
}
}
init(n,xhs);
manacher();
do_dp(n,ansxl,ansxr);
init(m,yhs);
manacher();
do_dp(m,ansyl,ansyr);
for(int i=ansxl;i<=ansxr;i++)
{
for(int j=ansyl;j<=ansyr;j++)
{
if(c[i][j]==0)
{
ans++;
bfs(i,j);
}
}
}
cout<<ans<<'\n';
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin>>t;
while(t--)solve();
return 0;
}