1、AOE-网介绍
我们在学习拓扑排序(如果没学,可以看看这篇博客:拓扑排序详解)的时候,已经接触了什么是AOV-网,AOV-网是优先考虑顶点的思路,而我们也同样可以优先考虑边,这个就是AOE-网的思路。
若在带权的有向无环图中,以顶点表示事件,以有向边表示活动,边上的权值表示活动的开销(如该活动持续的时间),则此带权的有向无环图称为AOE网。记住AOE-网只是比AOV-网多了一个边的权重,而且AOV-网一般是设计一个庞大的工程各个子工程实施的先后顺序,而我们的AOE-网就是不仅仅关系整个工程中各个子工程的实施的先后顺序,同时也关系整个工程完成最短时间。
因此,通常在AOE网中列出完成预定工程计划所需要进行的活动,每个活动计划完成的时间,要发生哪些事件以及这些事件与活动之间的关系,从而可以确定该项工程是否可行,估算工程完成的时间以及确定哪些活动是影响工程进度的关键。
AOE-网还有一个特点就是:只有一个起点(入度为0的顶点)和一个终点(出度为0的顶点),并且AOE-网有两个待研究的问题:
1.完成整个工程需要的时间
2.哪些活动是影响工程进度的关键
2、名词解释
关键路径:AOE-网中,从起点到终点最长的路径的长度(长度指的是路径上边的权重和)
关键活动:关键路径上的边
假设起点是vo,则我们称从v0到vi的最长路径的长度为vi的最早发生时间,同时,vi的最早发生时间也是所有以vi为尾的弧所表示的活动的最早开始时间,使用e(i)表示活动ai最早发生时间,除此之外,我们还定义了一个活动最迟发生时间,使用l(i)表示,不推迟工期的最晚开工时间。我们把e(i)=l(i)的活动ai称为关键活动,因此,这个条件就是我们求一个AOE-网的关键路径的关键所在了。
3、求关键路径的步骤
1.输入顶点数和边数,已经各个弧的信息建立图
2'从源点v1出发,令ve[0]=0;按照拓扑序列往前求各个顶点的ve。如果得到的拓扑序列个数小于网的顶点数n,说明我们建立的图有环,无关键路径,直接结束程序
3.从终点vn出发,令vl[n-1]=ve[n-1],按逆拓扑序列,往后求其他顶点vl值
4.根据各个顶点的ve和vl求每个弧的e(i)和l(i),如果满足e(i)=l(i),说明是关键活动。
4、python代码实现
class Stack():
"""栈类"""
def __init__(self):
self.stack = []
def Enstack(self, data):
"""入栈操作"""
self.stack.append(data)
def Destack(self):
"""出栈操作"""
return self.stack.pop()
def isEmpty(self):
"""判断栈是否为空"""
return not len(self.stack)
class Vertex(object):
"""创建Vertex类,用来存放顶点信息(包括data和firstEdge)"""
def __init__(self, data=None):
self.inDegree = 0
self.data = data
self.firstEdge = None
class EdgeNode(object):
""" 创建Edge类,用来存放边信息(包括adjVex和next);"""
def __init__(self, adjVex):
self.adjVex = adjVex
self.weight = None
self.next = None
class ALGraph():
"""有向图类"""
def __init__(self):
self.numNodes = 0
self.numEdges = 0
self.adjList = []
def createALGraph(self):
self.numNodes = int(input("输入顶点数:"))
self.numEdges = int(input("输入边数:"))
for i in range(self.numNodes): # 读入顶点信息,建立顶点表
v = Vertex()
self.adjList.append(v)
self.adjList[i].data = input("请输入顶点数据:")
self.adjList[i].inDgree = int(input("请输入此顶点的入度:"))
for k in range(self.numEdges): # 建立边表
i = int(input("请输入边(vi,vj)上的下标i:"))
j = int(input("请输入边(vi,vj)上的下标j:"))
w = int(input("请输入边(vi,vj)的权值:"))
e = EdgeNode(j) # 实例化边节点
e.next = self.adjList[i].firstEdge # 将e的指针指向当前顶点指向的节点
e.weight = w
self.adjList[i].firstEdge = e # 将当前顶点的指针指向e
def TopologicalSort(ALG):
count = 0 # 用于统计输出顶点的个数
stack = Stack() # 建栈将入度为0的顶点入栈
etv = [0 for _ in range(ALG.numNodes)] # 定义事件最早发生时间数组,并初始化
stack2 = Stack() # 实例化拓扑序列栈
for i in range(ALG.numNodes):
if ALG.adjList[i].inDgree == 0:
stack.Enstack(i) # 将入度为0的顶点入栈
while not stack.isEmpty(): # 若栈不为空
gettop = stack.Destack() # 出栈
count += 1 # 统计输出顶点数
stack2.Enstack(gettop) # 将弹出的顶点序号压入拓扑序列的栈
e = ALG.adjList[gettop].firstEdge
while e: # 对此顶点弧表遍历
k = e.adjVex
ALG.adjList[k].inDgree -= 1 # 将k号顶点邻接点的入度减1
if not ALG.adjList[k].inDgree: # 若入度为0则入栈,以便下次循环输出
stack.Enstack(k)
if etv[gettop] + e.weight > etv[k]: # 求各顶点事件的最早发生时间etv的值
etv[k] = etv[gettop] + e.weight
e = e.next
if count < ALG.numNodes: # count小于顶点数,说明存在环
return "ERROR"
else:
return etv, stack2
def CriticalPath(ALG):
etv, stack2 = TopologicalSort(ALG) # 求拓扑序列,计算数组etv和stack2的值
ltv = [etv[ALG.numNodes - 1] for _ in range(ALG.numNodes)] # 定义事件最晚发生时间数组并初始化
while not stack2.isEmpty(): # 计算ltv
gettop = stack2.Destack()
e = ALG.adjList[gettop].firstEdge
while e: # 对此顶点弧表遍历
k = e.adjVex
if ltv[k] - e.weight < ltv[gettop]: # 求各顶点事件最晚发生时间ltv
ltv[gettop] = ltv[k] - e.weight
e = e.next
for j in range(ALG.numNodes): # 求ete,lte和关键活动
e = ALG.adjList[j].firstEdge
while e: # 对此顶点弧表遍历
k = e.adjVex
ete = etv[j] # 活动最早发生时间
lte = ltv[k] - e.weight # 活动最晚发生时间
if ete == lte: # 两者相等即在关键路径上
print("<{} - {}> length: {}".format(ALG.adjList[j].data, ALG.adjList[k].data, e.weight))
e = e.next
if __name__ == '__main__':
ALG = ALGraph()
ALG.createALGraph()
print(ALG.adjList)
CriticalPath(ALG)
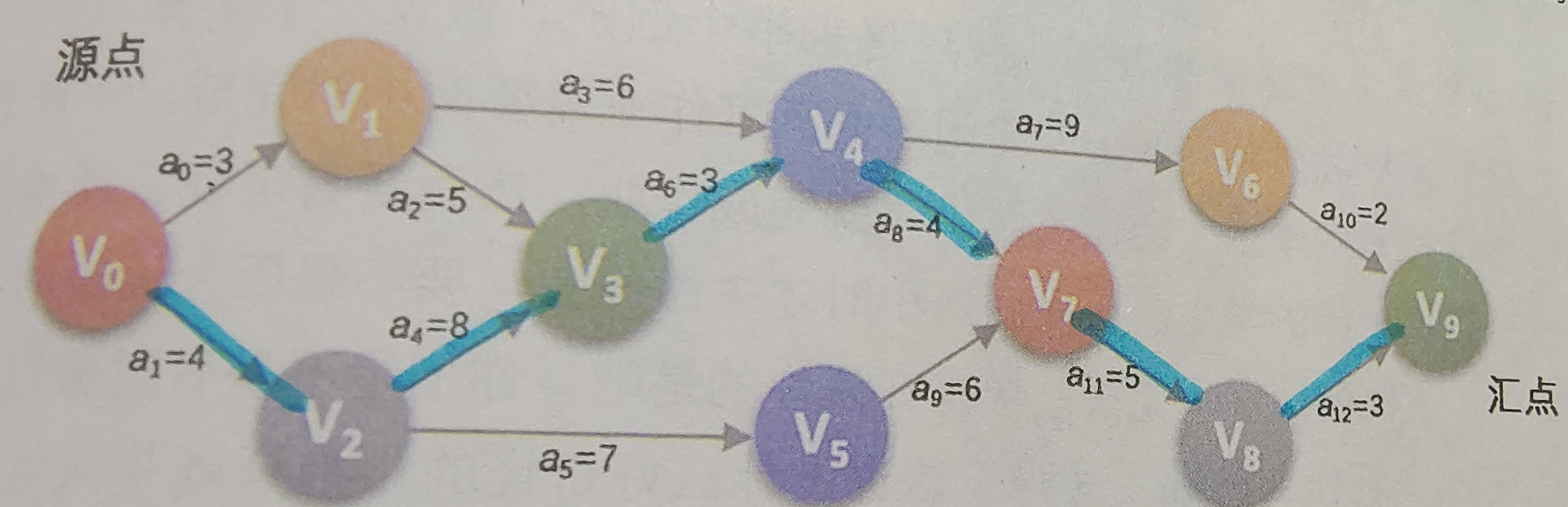
以下面的AOE网为例:
运行结果如下:
<v0 - v2> length: 4
<v2 - v3> length: 8
<v3 - v4> length: 3
<v4 - v7> length: 4
<v7 - v8> length: 5
<v8 - v9> length: 3