图论|网络流 总结

NOI 2018 归程

题目描述

本题的故事发生在魔力之都，在这里我们将为你介绍一些必要的设定。

魔力之都可以抽象成一个 \(n\) 个节点、\(m\) 条边的无向连通图（节点的编号从 \(1\) 至 \(n\)）。我们依次用 \(l,a\) 描述一条边的长度、海拔。

作为季风气候的代表城市，魔力之都时常有雨水相伴，因此道路积水总是不可避免的。由于整个城市的排水系统连通，因此有积水的边一定是海拔相对最低的一些边。我们用水位线来描述降雨的程度，它的意义是：所有海拔不超过水位线的边都是有积水的。

Yazid 是一名来自魔力之都的 OIer，刚参加完 ION2018 的他将踏上归程，回到他温暖的家。Yazid 的家恰好在魔力之都的 \(1\) 号节点。对于接下来 \(Q\) 天，每一天 Yazid 都会告诉你他的出发点 \(v\) ，以及当天的水位线 \(p\)。

每一天，Yazid 在出发点都拥有一辆车。这辆车由于一些故障不能经过有积水的边。Yazid 可以在任意节点下车，这样接下来他就可以步行经过有积水的边。但车会被留在他下车的节点并不会再被使用。
需要特殊说明的是，第二天车会被重置，这意味着：

• 车会在新的出发点被准备好。
• Yazid 不能利用之前在某处停放的车。

Yazid 非常讨厌在雨天步行，因此他希望在完成回家这一目标的同时，最小化他步行经过的边的总长度。请你帮助 Yazid 进行计算。

本题的部分测试点将强制在线，具体细节请见【输入格式】和【子任务】。

输入格式

单个测试点中包含多组数据。输入的第一行为一个非负整数 \(T\)，表示数据的组数。

接下来依次描述每组数据，对于每组数据：

第一行 \(2\) 个非负整数 \(n,m\)，分别表示节点数、边数。

接下来 \(m\) 行，每行 \(4\) 个正整数 \(u, v, l, a\)，描述一条连接节点 \(u, v\) 的、长度为 \(l\)、海拔为 \(a\) 的边。
在这里，我们保证 \(1 \leq u,v \leq n\)。

接下来一行 \(3\) 个非负数 \(Q, K, S\) ，其中 \(Q\) 表示总天数，\(K \in {0,1}\) 是一个会在下面被用到的系数，\(S\) 表示的是可能的最高水位线。

接下来 \(Q\) 行依次描述每天的状况。每行 \(2\) 个整数 \(v_0, p_0\) 描述一天：

• 这一天的出发节点为 \(v = (v_0 + K \times \mathrm{lastans} - 1) \bmod n + 1\)。
• 这一天的水位线为 \(p = (p_0 + K \times \mathrm{lastans}) \bmod (S + 1)\)。

其中 \(\mathrm{lastans}\) 表示上一天的答案（最小步行总路程）。特别地，我们规定第 \(1\) 天时 \(\mathrm{lastans} = 0\)。
在这里，我们保证 \(1 \leq v_0 \leq n\)，\(0 \leq p_0 \leq S\)。

对于输入中的每一行，如果该行包含多个数，则用单个空格将它们隔开。

slove

讲完一直说要做，一直没做，拖到了现在。

kruskal重构树

在用kruskal算法时，将边看作点，合并边时合并点，但不进行路径压缩以保持二叉树的形状。

• 树上除叶子结点以外的点都对应着原来生成树中的边，叶子结点就是原来生成树上的节点。

• 由于新点的创建顺序与原来生成树上边权的大小有关，可以发现，从每个点到根节点上除叶子结点外按顺序访问到的点的点权是单调的。

• 由于kruskal算法是贪心算法，实际上它是一个堆

  我们按海拔排序，建立最小生成树，使得重构树是一个小根堆。发现如果重构树上的一个点没有被淹没，那么它的子树中的所有点一定不会被淹没，也就是说在子树中的边行走不会消耗代价直到走到第一个积水节点（也就是子树的祖先）

  处理出来终点到每个点的最短路，对于每次询问的起点，树上倍增找出临界点，然后答案就是临界点到终点的距离。

  SPFA被卡了

狼抓兔子

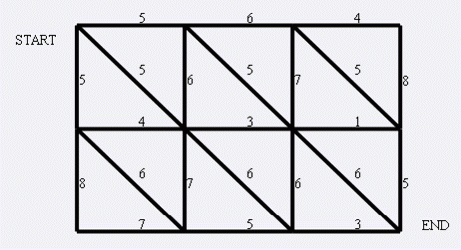
一张如下的图，要求最小割。

n行m列，n*m小于1000

由于数据太水？，所以可以跑最大流（dinic）水过去，做法很简单。但是这样显然不是正解

考虑建立一个这样的图：

[这里缺一张图]

然后跑一遍最短路，就是最小割，然后就做完了。

杀人游戏

一张有向图，n个节点，一个杀手剩下都是平民。问一个平民可以得知所有出边连向点的身份，问杀手会被干掉。求得知所有人状态而不被干掉的概率。

首先有一个性质，在同一个强连通分量里，问其中的一个人就可以问出所有人状态，所以可以缩点，把一个scc看作一个点。

然后我们观察一下，好像只需要问所有没有入边（也就是无法从其他人那里得知自己的状态）的点就可以得知整张图的状态，但是实际上不见得。

如果得知了n-1个点的状态，那么第n个点就不用问了，需要特判

最后的答案就是1 - 问了的点数/总点数