实现有些傻瓜,喜提时空双最劣解。

首先要判断一个点是否在多边形内,一个比较好的方法是从这个点向上引一条射线,若和奇数条边相交就在多边形内,否则在多边形外。
二维信息,考虑用树套树维护。把多边形的每一条边都扔到它 \(x\) 坐标范围的线段树节点里,即线段树节点 \((l,r)\) 里面维护了 \(x\) 坐标一端点小于 \(l\),一端点大于 \(r\) 的边。 由于边不相交,所以一个节点中的所有线段是有偏序关系的,用平衡树维护。查询的时候直接查询其 \(x\) 坐标对应节点到线段树根路径上的所有平衡树,直接计算在它上面的线段数量即可。
下面是一些细节:
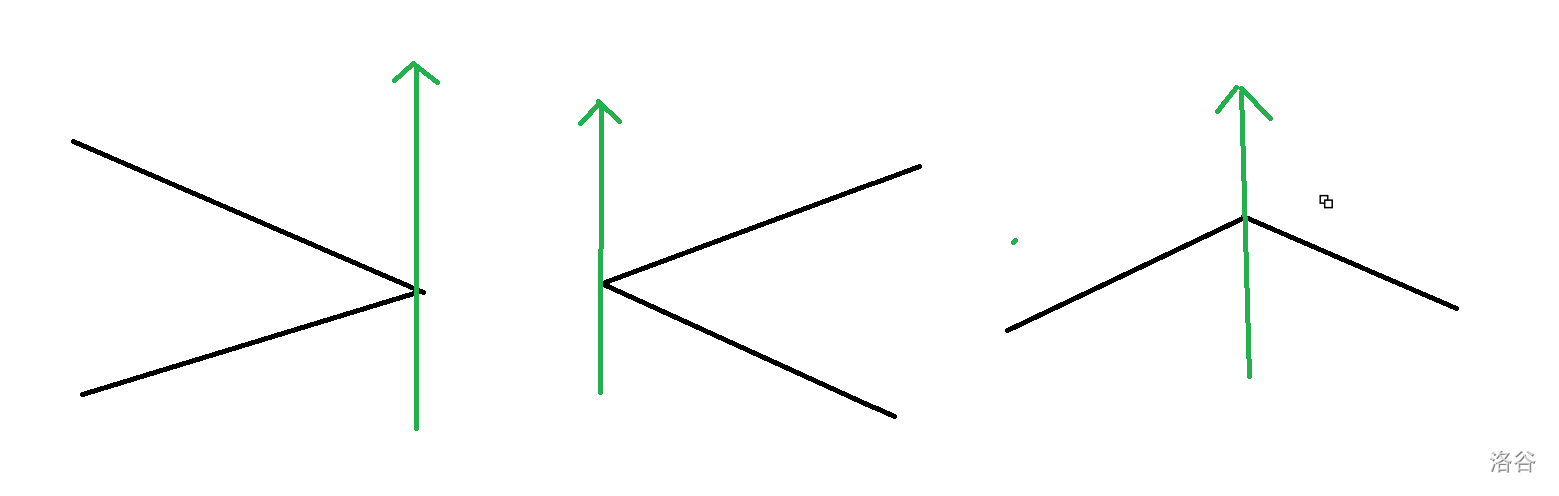
如图,对于经过一个顶点的情况,前两种情况奇偶性不改变,而第三种情况改变了。因此我们可以将所有线段设成左闭右开的形式(注意这里不是按顺时针顺序,而是按 \(x\) 坐标大小区分左右)。
但如果这样的话,上图第一种情况中,如果询问的点就在右面的尖上,那么因为线段是左闭右开的那么它就不会被正确判断成在边界上。这个也好处理,用 map 存一下多边形上所有点,特判即可。
再就是关于比较两个线段(或比较线段和点)的上下关系,我写的是直接带两边的点值进去,带两个是因为有可能有两个线段有公共点的情况。
最后,本题卡空间,不要开太大数组。原则上需要离散化,但是我没离散化也过了。
代码
#include<bits/stdc++.h>
inline void rd(){}
template<typename T,typename ...U>
inline void rd(T &x,U &..args){
int ch=getchar();
T f=1;x=0;
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x*=f;rd(args...);
}
#define pii std::pair<int,int>
#define mkp std::make_pair
const int N=5e4+5,INF=1e9;
const double eps=1e-9;
int n,m;
struct node{
int x,y;
node(){x=y=0;}
node(int _x,int _y){x=_x,y=_y;}
bool friend operator<(node x,node y){return x.x==y.x?x.y<y.y:x.x<y.x;}
}p[N];
struct Edge{
int x1,x2,y1,y2;
Edge(){x1=x2=y1=y2=0;};
Edge(node a,node b){
if(a.x>b.x)std::swap(a,b);
x1=a.x,x2=b.x,y1=a.y,y2=b.y;}
Edge(int _x1,int _y1,int _x2,int _y2){x1=_x1,x2=_x2,y1=_y1,y2=_y2;}
inline double Val(int x){return 1.L*(y2-y1)*(x-x1)/(x2-x1)+y1;}
bool friend operator<(Edge x,Edge y){
int pos1=std::max(x.x1,y.x1),pos2=std::min(x.x2,y.x2);
return x.Val(pos1)+eps<y.Val(pos1)||x.Val(pos2)+eps<y.Val(pos2);
}
bool friend operator<=(Edge x,Edge y){
int pos1=std::max(x.x1,y.x1),pos2=std::min(x.x2,y.x2);
return x.Val(pos1)<y.Val(pos1)+eps||x.Val(pos2)+eps<y.Val(pos2)+eps;
}
bool friend operator<(Edge x,node y){
return x.Val(y.x)+eps<1.0*y.y;
}
bool friend operator==(Edge x,node y){
return x.Val(y.x)-1.0*y.y<=eps;
}
}v[N];
std::mt19937 mtrd(time(0));
namespace BST{
int ch[N*60][2],sz[N*60],pri[N*60],cnt;
Edge v[N*60];
struct BST{
int rt;
BST(){rt=0;}
inline int NewNode(Edge x){
pri[++cnt]=mtrd();
sz[cnt]=1;v[cnt]=x;
return cnt;
}
inline void PushUp(int i){sz[i]=sz[ch[i][0]]+sz[ch[i][1]]+1;}
int Merge(int x,int y){
if(!x||!y)return x+y;
if(pri[x]<pri[y]){
ch[x][1]=Merge(ch[x][1],y);
return PushUp(x),x;
}
else{
ch[y][0]=Merge(x,ch[y][0]);
return PushUp(y),y;
}
}
void Split(int now,Edge k,int &x,int &y){
if(!now)return x=y=0,void();
if(v[now]<k)x=now,Split(ch[now][1],k,ch[now][1],y);
else y=now,Split(ch[now][0],k,x,ch[now][0]);
PushUp(now);
}
void Split(int now,node k,int &x,int &y){
if(!now)return x=y=0,void();
if(v[now]<k)x=now,Split(ch[now][1],k,ch[now][1],y);
else y=now,Split(ch[now][0],k,x,ch[now][0]);
PushUp(now);
}
void Split(int now,int k,int &x,int &y){
if(!now)return x=y=0,void();
if(sz[ch[now][0]]>=k)y=now,Split(ch[now][0],k,x,ch[now][0]);
else x=now,Split(ch[now][1],k-sz[ch[now][0]]-1,ch[now][1],y);
PushUp(now);
}
inline void Insert(Edge x){
int a,b;
Split(rt,x,a,b);
rt=Merge(Merge(a,NewNode(x)),b);
}
inline Edge Find(int x){
while(ch[x][0])x=ch[x][0];
return v[x];
}
inline int Get(node x){
int a,b;
Split(rt,x,a,b);
int sum=sz[b];
Edge tmp=Find(b);
if(tmp==x)sum+=1e7;
rt=Merge(a,b);
return sum;
}
inline void Delete(Edge x){
int a,b,c;
Split(rt,x,a,b);Split(b,1,b,c);
rt=Merge(a,c);
}
};
}
namespace SegT{
struct Seg{
BST::BST t;
int ls,rs;
}t[N*45];
int cnt=0,rt=0;
void Update(int &i,int l,int r,int L,int R,Edge k){
if(!i)i=++cnt;
if(L<=l&&r<=R)return t[i].t.Insert(k),void();
int mid=(l+r)>>1;
if(L<=mid)Update(t[i].ls,l,mid,L,R,k);
if(R>mid)Update(t[i].rs,mid+1,r,L,R,k);
}
void Delete(int &i,int l,int r,int L,int R,Edge k){
if(!i)i=++cnt;
if(L<=l&&r<=R)return t[i].t.Delete(k),void();
int mid=(l+r)>>1;
if(L<=mid)Delete(t[i].ls,l,mid,L,R,k);
if(R>mid)Delete(t[i].rs,mid+1,r,L,R,k);
}
int Query(int i,int l,int r,node x){
if(!i)return 0;
if(l==r)return t[i].t.Get(x);
int mid=(l+r)>>1;
if(x.x<=mid)return Query(t[i].ls,l,mid,x)+t[i].t.Get(x);
else return Query(t[i].rs,mid+1,r,x)+t[i].t.Get(x);
}
}
std::map<node,int> ndmp;
inline void Add(Edge x){SegT::Update(SegT::rt,0,INF,x.x1,x.x2-1,x);}
inline void Del(Edge x){SegT::Delete(SegT::rt,0,INF,x.x1,x.x2-1,x);}
int q[3][2],ans,lstx,lsty;
signed main(){
rd(n);
for(int i=1;i<=n;i++)rd(p[i].x,p[i].y),ndmp[p[i]]=1;
for(int i=1;i<=n;i++){
node nd1=p[i],nd2=p[i%n+1];
if(nd1.x>nd2.x)std::swap(nd1,nd2);
v[i].x1=nd1.x,v[i].x2=nd2.x;
v[i].y1=nd1.y,v[i].y2=nd2.y;
Add(v[i]);
}
rd(m);
if(ndmp[node(0,0)])ans=2;
else ans=1;
for(int i=1;i<=m;i++){
int op,r,sum=0;node a,b,c;
rd(op);
if(op==0){
rd(r);
for(int i=0;i<3;i++)rd(q[i][0],q[i][1]);
lstx=(1ll*lstx*r+q[ans][0])%INF;
lsty=(1ll*lsty*r+q[ans][1])%INF;
if(ndmp[node(lstx,lsty)])ans=2;
else{
sum=SegT::Query(SegT::rt,0,INF,node(lstx,lsty));
if(sum>1e7)ans=2;
else if(sum&1)ans=0;
else ans=1;
}
puts((ans==2?"ed":(ans==1?"out":"in")));
}else{
rd(a.x,a.y,b.x,b.y,c.x,c.y);
Del(Edge(a,b));Add(Edge(a,c));Add(Edge(b,c));
ndmp[c]=1;
}
}
return 0;
}