首页 > 其他分享 >蓝书 0x40

蓝书 0x40

时间：2024-12-15 11:43:36浏览次数：3  
标签：tmp int LL tr mid 0x40 蓝书 区间

0x42 树状数组

何为树状数组？

首先，树状数组是用来维护序列的前缀和的。

其次，我们要知道树状数组是如何将大区间拆分成一堆小区间的。

比如 \(7 = 111_{(2)}\)，我们可以将其拆分为 \([1,4], [5, 6], [7, 7]\)，再比如 \(12 = 1100_{2}\)，我们可以将其拆分为 \([1, 8],[9, 12]\)。

所以对于一个数 \(x\)，我们每次可以将其拆分为 \([x - lowbit(x) + 1, x]\) 的小区间，然后将 \(x = x - lowbit(x)\)。

那么对于树状数组 \(tr[x]\) 来说，它存的就是 \([x - lowbit(x) + 1, x]\) 的和，比如 \(tr[6]\) 存的是 \([5, 6]\)。

如何查询呢？

假设我们要查询 \([1, x]\) 的前缀和，我们可以从 \(x\) 开始：

  1. 加上 \(tr[x]\)
  2. 令 \(x = x - lowbit(x)\)
  3. 循环以上操作，直到 \(x = 0\)。

一个简单的例子：\([1,15]\) 的前缀和就等于 \(tr[15] + tr[14] + tr[12] + tr[8]\)

如何单点增加呢？

假设我们要在 \(A_x\) 上加 \(y\) 我们只要让所有包含 \(A_x\) 的 \(tr\) 加上 \(y\) 即可。集体操作如下：

  1. \(tr[x]\) 加上 \(y\)
  2. 令 \(x = x + lowbit(x)\)
  3. 循环以上操作，直到 \(x > n\)。

如何建树呢？

假设要对于 \(A_1\sim A_n\) 构造一个树状数组，那么我们只要对于每个 \(i\) 都做一次单点修改，加上 \(A_i\) 即可。

如何区间修改呢？

我们可以使用差分，用树状数组维护差分数组 \(b\)，每次 \(b_l + d, b_{r + 1} - d\)，就相当于 \(add(l, d)\) 和 \(add(r + 1, -d)\)。

如何区间查询呢？

img

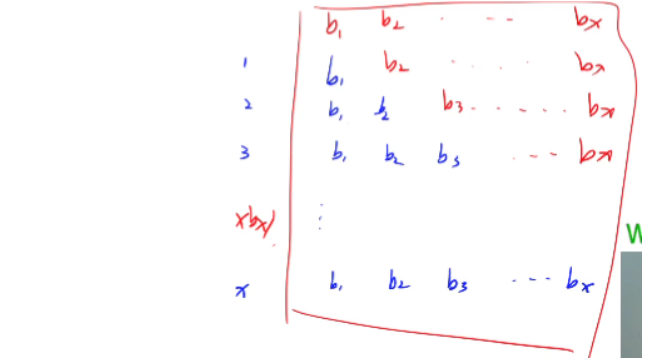
我们观察 y 总画的图，其中 \(b\) 是差分数组。我们发现，蓝色就等于一整个方框减去红色，即：

\((x+1)\sum^{n}_{i = 1}b_i - \sum^{n}_{i = 1}i \times b_i\)

我们可以用两个树状数组分别维护 \(\sum^{n}_{i = 1}b_i\) 和 \(\sum^{n}_{i = 1}i \times b_i\)。

树状数组可以求逆序对

假设有一个序列 \(A\)，我们在 \(A\) 的值域范围上构造树状数组，即对于每个 \(A_i\) 执行一遍 \(add(A_i, 1)\)。

统计逆序对的时候，我们只要返回 \(query(A_i - 1)\) 即可。

这个复杂度是 \(O(N+M)logM\) 的，其中 \(M\) 是值域大小。

来看一些蓝书上的例题。

241. 楼兰图腾 - AcWing题库

我们运用类似于求逆序对的思路，对于 \(A_i\)，求出 \(A_1 \sim A_{i - 1}\) 内小于它的数的数量 \(small1[i]\) 和大于的数量 \(big1[i]\)，再倒着求出 \(A_{i + 1} \sim A_n\) 内的 \(small2[i]\) 和 \(big2[i]\)。

我们以 ^ 为例，它的数量就是 \(\sum^{n}_{i = 1} small1[i] \times small2[i]\)。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 200010;
int n, a[N];
LL tr[N], big[N], small[N];

int lowbit(int x) {
    return x & -x;
}

void add(int x, int c) {
    for (; x <= n; x += lowbit(x)) tr[x] += c;
}

LL query(int x) {
    LL res = 0;
    for (; x; x -= lowbit(x)) res += tr[x];
    return res;
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++) {
        int x = a[i];
        big[i] = query(n) - query(x);
        small[i] = query(x - 1);
        add(x, 1);
    }
    
    memset(tr, 0, sizeof tr);
    LL res1 = 0, res2 = 0;
    for (int i = n; i; i --) {
        int x = a[i];
        res1 += big[i] * (query(n) - query(x));
        res2 += small[i] * query(x - 1);
        add(x, 1);
    }
     
    printf("%lld %lld\n", res1, res2);
    return 0;
}

242. 一个简单的整数问题 - AcWing题库

就是上文中提到的区间修改+单点查询。

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m;
int a[N], tr[N];

int lowbit(int x) {
    return x & -x;
}

void add(int x, int c) {
    for (; x <= n; x += lowbit(x)) tr[x] += c;
}

int query(int x) {
    int res = 0;
    for (; x; x -= lowbit(x)) res += tr[x];
    return res;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++) {
        int b = a[i] - a[i - 1];
        add(i, b);
    }
    
    while (m --) {
        char op[2]; 
        scanf("%s", op);
        if (*op == 'C') {
            int l, r, d; scanf("%d%d%d", &l, &r, &d);
            add(l, d); add(r + 1, -d);
        } else {
            int x; scanf("%d", &x);
            printf("%d\n", query(x));
        }
    }
    return 0;
}

243. 一个简单的整数问题2 - AcWing题库

区间查询+区间修改

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100010;
int n, m, a[N]; 
LL tr1[N], tr2[N];

int lowbit(int x) {
    return x & -x;
} 

void add(LL tr[], int x, LL c) {
    for (; x <= n; x += lowbit(x)) tr[x] += c;
}

LL query(LL tr[], int x) {
    LL res = 0;
    for (; x; x -= lowbit(x)) res += tr[x];
    return res;
}

LL prefix_sum(int x) {
    return query(tr1, x) * (x + 1) - query(tr2, x); 
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++) {
        int b = a[i] - a[i - 1];
        add(tr1, i, b);
        add(tr2, i, (LL)i * b);
    }
    
    while (m --) {
        char op[2]; int l, r, d;
        scanf("%s%d%d", op, &l, &r);
        if (*op == 'C') {
            scanf("%d", &d);
            add(tr1, l, d); add(tr2, l, (LL)l * d);
            add(tr1, r + 1, -d); add(tr2, r + 1, (LL)(r + 1) * -d);
        } else {
            printf("%lld\n", prefix_sum(r) - prefix_sum(l - 1));
        }
    }
    
    return 0;
}

244. 谜一样的牛 - AcWing题库

很有意思的一道题。

我们发现对于 \(i\) 来说，它对应的牛就应该是剩下未选择的牛中第 \(A_i + 1\) 大的牛。

什么是未选择的牛？假设当前牛为 \(1 \sim 5\)，且已经选择了 \(2, 4\)，那么 \(1,3,5\) 就是未选择的牛，\(3\) 就是第二大的牛。

想通了之后就很好维护了，我们维护一个树状数组，最开始从 \(1\sim n\) 执行 \(add(i, 1)\)，然后每选择一只牛 \(x\) 就 \(add(x, -1)\)。我们发现 \(query(x)\) 就是当前 \(1\sim x\) 中未选择牛的数量。找第 \(A_i + 1\) 大的牛就显然可以二分。

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, a[N];
int tr[N], ans[N];

int lowbit(int x) {
    return x & -x;
}

void add(int x, int c) {
    for (; x <= n; x += lowbit(x)) tr[x] += c; 
}

int query(int x) {
    int res = 0;
    for (; x; x -= lowbit(x)) res += tr[x];
    return res;
}

int main() {
    scanf("%d", &n);
    for (int i = 2; i <= n; i ++) scanf("%d", &a[i]);
    for (int i = 1; i <= n; i ++) add(i, 1);
    
    for (int i = n; i; i --) {
        int l = 1, r = n;
        while (l < r) {
            int mid = l + r >> 1;
            if (query(mid) < a[i] + 1) l = mid + 1;
            else r = mid;
        }
        add(l, -1);
        ans[i] = l;
    }
    
    
    for (int i = 1; i <= n; i ++) printf("%d\n", ans[i]);
    
    return 0;
}

0x43 线段树

何为线段树？

线段树和树状数组不同，它维护的是一个个子序列。

img

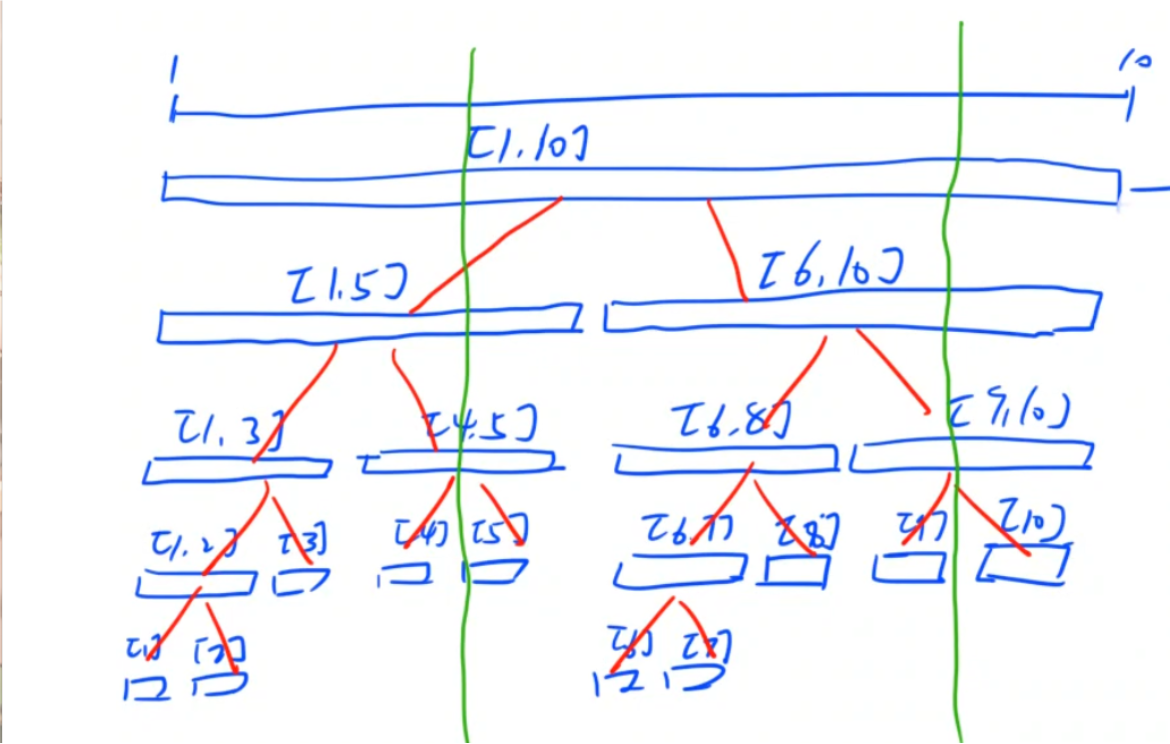
如上图，对于一个区间 \([l, r]\)，它的左儿子就是 \([l, mid]\)，右儿子就是 \([mid + 1, r]\)，其中 \(mid = \frac{l+r}{2}\)。

我们可以给线段树上的每一个结点编号，假设父节点编号为 \(x\)，左儿子编号就是 \(x\times2\)，右儿子编号就是 \(x\times2+1\)。

struct Stree {
    int l, r, v;
} tr[N * 4];

以上代码是最简单的线段树，其中 \(l, r\) 为区间的左右端点，\(v\) 为区间内所有数的最大值。

然后我们来说如何维护线段树。

首先，建树。

我们可以参照上图，我们从根节点开始，每次分别递归左儿子和右儿子，直到叶节点。此时它的最大值就应该是它本身。然后我们回溯到父节点，由于我们已经对它的儿子都做过了，所以我们可以用儿子的值求出父亲，即父亲的最大值可以通过儿子的最大值推出来。

void pushup(int u) {
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}
void build(int u, int l, int r) {
    tr[u].l = l, tr[u].r = r;
    if (l == r) return;
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    pushup(u);
}

build(1, 1, n);

以上代码中，\(build\) 就是建树，\(pushup\) 就是用儿子来更新父亲。

有的时候我们可能会这样写 \(build\)。

void build(int u, int l, int r) {
    if (l == r) tr[u] = {l, r, w[r]};
    else {
        int mid = l + r >> 1;
        tr[u] = {l, r};
        build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

此时请注意 \(else\) 中也要为 \(tr[u]\) 所对应区间赋值。

\(build\) 是 \(O(nlogn)\) 的

接着，我们考虑单点修改。

假设当前我们要修改下标为 \(x\) 的数，那么从根节点开始，对于一个父节点， \(x\) 一定在它的左儿子或是右儿子。我们只要从中选择一个即可。

修改完儿子后，我们同样要 \(pushup\)。

void modify(int u, int x, int val) {
    if (tr[u].l == x && tr[u].r == x) {
        tr[u].v = val;
    } else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, val);
        if (x > mid) modify(u << 1 | 1, x, val);
        pushup(u);
    }
}

\(modify\) 显然是 \(O(logn)\) 的。

然后是区间查询。

区间查询就是对于一个区间 \([l, r]\) 询问它的最大值，总和，或是其它线段树维护的值，这里以最大值为例。

对于线段树上的一个结点 \(u\)，我们可以分四种情况：

  1. \(u\) 存储的区间被 \([l, r]\) 包含，那么我们直接范围 \(u\) 即可。
  2. \(u\) 属于 \([l, mid]\)，那么我们递归左儿子。
  3. \(u\) 属于 \([mid + 1, r]\)，我们递归右儿子。
  4. \(u\) 横跨左右儿子，我们左右一起递归。

下面是一个简便写法。

int query(int u, int l, int r) {
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].v;
    int mid = tr[u].l + tr[u].r >> 1;
    int s = 0;
    if (l <= mid) s = query(u << 1, l, r);
    if (r > mid) s = max(s, query(u << 1 | 1, l, r));
    return s;
}

为什么要分四种情况讨论呢？因为有的题目需要我们维护一些横跨两个子区间的信息，所以需要在第四种情况时进行额外的操作。

由于答案一般能够分成 \(O(logn)\) 个区间，所以 \(query\) 的时间复杂度是 \(O(logn)\) 的。

然后是比较困难的区间修改。

我们首先可以想到对于区间的每个点进行单点修改，但这样过于慢。我们发现，如果对一段区间进行修改后，它的儿子的值也都会变化，所以在最坏情况下我们会遍历整棵树。

这里我们引入懒标记，即为了偷懒而生的标记。我们在维护线段树上结点的信息的同时，再维护一个 \(add\)（这里以区间增加为例），意思是我们需要给该结点的所有儿子都加上 \(add\)（儿子是一个序列，如果长为 \(k\)，那就相当于序列中的每个数都加 \(add\)，即总和加 \(k\times add\)）。

我们在执行区间修改的时候，如果某个结点表示的区间被询问的区间包含，那么就修改它的懒标记，同时更改这个区间的和。

void pushdown(int u) {
    STree &left = tr[u << 1], &right = tr[u << 1 | 1], &root = tr[u];
    if (root.add) {
        // 给区间内的每个数加上 add，那么区间的总和就要加上区间长度 * add
        left.add += root.add, left.s += (LL)(left.r - left.l + 1) * root.add;
        right.add += root.add, right.s += (LL)(right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}
void modify(int u, int l, int r, int d) {
    if (l <= tr[u].l && tr[u].r <= r) {
        tr[u].add += d;
        tr[u].s += (LL)(tr[u].r - tr[u].l + 1) * d;
    } else {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, d);
        if (r > mid) modify(u << 1 | 1, l, r, d);
        pushup(u);
    }
}
LL query(int u, int l, int r) {
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].s;
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1; 
    LL res = 0;
    if (l <= mid) res += query(u << 1, l, r);
    if (r > mid) res += query(u << 1 | 1, l, r);
    return res;
}

我们发现在 \(modify\) 中多出了一个 \(pushdown\)，它的含义就是将父亲的懒标记下传，因为此时我们要遍历子区间了。

同时查询操作也要加上 \(pushdown\) 操作。

245. 你能回答这些问题吗 - AcWing题库

我们考虑在线段树中维护 \(lmax\)，意思是当前区间最大连续前缀和，同样维护 \(rmax\)。

此时父节点的最大连续子段和就是子节点的最大连续子段和，以及左儿子的 \(rmax\) 加上右儿子的 \(lmax\) 的最大值。

#include <bits/stdc++.h>
using namespace std;
const int N = 500010;
int n, m;
int a[N];

struct Stree {
    int l, r, s, smax, lmax, rmax;
} tr[N * 4];

void pushup(Stree &u, Stree &a, Stree &b) {
    u.s = a.s + b.s;
    u.lmax = max(a.lmax, a.s + b.lmax);
    u.rmax = max(b.rmax, a.rmax + b.s);
    u.smax = max({a.smax, b.smax, a.rmax + b.lmax});
}

void pushup(int u) {
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r) {
    if (l == r) tr[u] = {l, r, a[r], a[r], a[r], a[r]};
    else {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

void modify(int u, int x, int v) {
    if (tr[u].l == x && tr[u].r == x) tr[u].s = tr[u].smax = tr[u].lmax = tr[u].rmax = v;
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

Stree query(int u, int l, int r) {
    if (tr[u].l >= l && tr[u].r <= r) return tr[u];
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (r <= mid) return query(u << 1, l, r);
        else if (l > mid) return query(u << 1 | 1, l, r);
        else {
            auto a = query(u << 1, l, r), b = query(u << 1 | 1, l, r);
            Stree c;
            pushup(c, a, b);
            return c;
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);
    build(1, 1, n);
    
    while (m --) {
        int op, l, r;
        scanf("%d%d%d", &op, &l, &r);
        if (op == 1) {
            if (l > r) swap(l, r);
            printf("%d\n", query(1, l, r).smax);
        } else {
            modify(1, l, r);
        }
    }
    
    return 0;
}

246. 区间最大公约数 - AcWing题库

由更相减损术我们可以知道：

\[\gcd(w[i], w[i + 1], w[i + 2], ..., w[j]) = gcd(w[i], w[i + 1] - w[i], w[i + 2] - w[i - 1], ..., w[j] - w[j - 1]) \]

这其实是差分的形式，这启发我们用线段树维护差分。

具体我们可以在线段树中维护差分，具体地我们维护一个 \(s\) 表示 \([l, r]\) 的差分和，再维护一个 \(d\) 表示 \([l, r]\) 的最大公约数。

那么原来的式子就可以表示为 \(gcd(w[i], gcd(b[i + 1], ..., b[j])) = gcd(query(1, i).s, query(i + 1, j).d)\)，其中 \(query\) 返回的是一整个线段树结点。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 500010;
int n, m;
LL w[N];

struct Stree {
    int l, r; 
    LL s, d;
} tr[N * 4];

LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : abs(a);
}

void pushup(Stree &u, Stree &l, Stree &r) {
    u.s = l.s + r.s;
    u.d = gcd(l.d, r.d);
}

void pushup(int u) {
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

void build(int u, int l, int r) {
    if (l == r) tr[u] = {l, r, w[r] - w[l - 1], w[r] - w[l - 1]};
    else {
        tr[u] = {l, r}; 
        int mid = l + r >> 1;
        build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

void modify(int u, int x, LL v) {
    if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, tr[u].s + v, tr[u].s + v};
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        pushup(u);
    }
}

Stree query(int u, int l, int r) {
    if (tr[u].l >= l && tr[u].r <= r) return tr[u];
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l > mid) return query(u << 1 | 1, l, r);
        else if (r <= mid) return query(u << 1, l, r);
        else {
            auto a = query(u << 1, l, r), b = query(u << 1 | 1, l, r);
            Stree c;
            pushup(c, a, b);
            return c;
        }
    }
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%lld", &w[i]);
    build(1, 1, n);

    while (m --) {
        char op[2]; int l, r; LL d;
        scanf("%s%d%d", op, &l, &r);
        if (*op == 'Q') {
            if (l == r) printf("%lld\n", query(1, 1, l).s);
            else {
                auto a = query(1, 1, l), b = query(1, l + 1, r);
                printf("%lld\n", gcd(a.s, b.d));
            }
        } else {
            scanf("%lld", &d);
            modify(1, l, d); 
            if (r + 1 <= n) modify(1, r + 1, -d);
        }
    }

    return 0;
}

243. 一个简单的整数问题2 - AcWing题库

懒标记模板。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100010;
int n, m, w[N];

struct STree {
    int l, r;
    LL s, add;
} tr[N * 4];

void pushup(int u) {
    tr[u].s = tr[u << 1].s + tr[u << 1 | 1].s;
}

void pushdown(int u) {
    STree &left = tr[u << 1], &right = tr[u << 1 | 1], &root = tr[u];
    if (root.add) {
        left.add += root.add, left.s += (LL)(left.r - left.l + 1) * root.add;
        right.add += root.add, right.s += (LL)(right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}

void build(int u, int l, int r) {
    if (l == r) tr[u] = {l, r, w[r], 0};
    else {
        int mid = l + r >> 1;
        tr[u] = {l, r};
        build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);
        pushup(u);
    }
}

void modify(int u, int l, int r, int d) {
    if (l <= tr[u].l && tr[u].r <= r) {
        tr[u].add += d;
        tr[u].s += (LL)(tr[u].r - tr[u].l + 1) * d;
    } else {
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, d);
        if (r > mid) modify(u << 1 | 1, l, r, d);
        pushup(u);
    }
}

LL query(int u, int l, int r) {
    if (l <= tr[u].l && tr[u].r <= r) return tr[u].s;
    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1; 
    LL res = 0;
    if (l <= mid) res += query(u << 1, l, r);
    if (r > mid) res += query(u << 1 | 1, l, r);
    return res;
}

int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++) scanf("%d", &w[i]);
    build(1, 1, n);
    while (m --) {
        char op[2]; int l, r;
        scanf("%s%d%d", op, &l, &r);
        if (*op == 'C') {
            int d; scanf("%d", &d);
            modify(1, l, r, d);
        } else {
            printf("%lld\n", query(1, l, r));
        }
    }
    return 0;
}

何为扫描线？

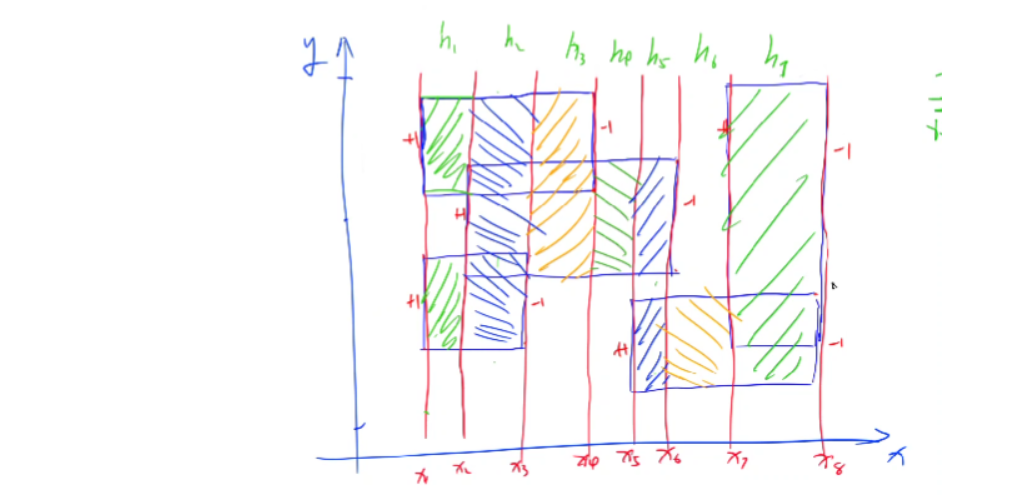
假设当前平面内有一堆的矩形，我们要统计它们的面积（不能重复），那么我们就可以像下图一样，用一条平行 \(y\) 轴的扫描线从左往右，扫。根据下图，总面积就应该是 \(\sum^{2n - 1}_{i = 1}h_i \times (x_{i + 1} - x_i)\)，其中 \(n\) 为矩形的数量，\(h_i\) 为扫描线上覆盖有矩形的长度。

具体地，我们把每扫到一个矩形的左宽，就把左宽覆盖的区间 \(+1\)，扫到右宽就 \(-1\)，这样就可以算出 \(h_i\)。

我们发现该操作设计区间修改和区间查询，所以我们考虑用线段树加速。

线段树中存储 \(cnt\) 表示直接完全覆盖此区间的矩形数量，\(len\) 表示此区间被矩形覆盖的长度。

并且注意，线段树上的每个叶节点存的都是区间，所以需要注意坐标。

根据以上的存储方式，可能会出现子节点的 \(cnt\) 大于父节点的 \(cnt\) 的情况。

我们再考虑 \(pushup\) 操作如何写。分三种情况：

  1. \(cnt \ne 0\)，说明该区间被完全覆盖，\(len\) 就为该区间的长度。
  2. \(cnt = 0\)，且 \(l \ne r\)，可以用左儿子和右儿子来更新自己。
  3. \(cnt = 0\)，且 \(l = r\)，不合法，无用线段，\(len = 0\)

我们可以通过一些手段证明 \(pushdown\) 某些时候是不用写的。（另外一些时候比如第二道例题要写，下文会提到）。

引用的证明：

此时 \(cnt\) 表达的含义：当前区间被覆盖的次数，跟其它节点无关。

可以发现，因为对于修改区间 \([l, r]\) 操作，是一对一对的。

所以，一个节点代表的区间被覆盖的次数不需要继承其父亲信息的情况。

因此需要去掉 \(pushDown\)。

img

我们 \(Atlantis\) 一题为例。

247. 亚特兰蒂斯 - AcWing题库

在上文的思路上，由于本题坐标可能有小数，所以需要进行离散化。

#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
int n;
vector<double> tmp;

struct Segment {
    double x, y1, y2;
    int k;
    
    bool operator < (const Segment &t) const{
        return x < t.x;
    }
} segs[N * 2];

struct Stree {
    int l, r, cnt;
    double len;
} tr[N * 8];

// tmp 存的是小数，它在 tmp 中的位置就是离散化的值
// find 查找的是某个小数被映射到了什么位置
int find(double v) {
    return lower_bound(tmp.begin(), tmp.end(), v) - tmp.begin();
}

void pushup(int u) {
    if (tr[u].cnt) {
        tr[u].len = tmp[tr[u].r + 1] - tmp[tr[u].l];
    } else if (tr[u].l != tr[u].r) {
        tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
    } else {
        tr[u].len = 0;
    }
}

void build(int u, int l, int r) {
    if (l == r) tr[u] = {l, r, 0, 0};
    else {
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);
    }
}

void modify(int u, int l, int r, int d) {
    if (l <= tr[u].l && tr[u].r <= r) {
        tr[u].cnt += d; 
        pushup(u);
    } else {
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, d);
        if (r > mid) modify(u << 1 | 1, l, r, d);
        pushup(u);
    }
}

int main() {
    
    int T = 0;
    while (scanf("%d", &n), n) {
        tmp.clear();
        for (int i = 1, j = 0; i <= n; i ++) {
            double x_1, y_1, x_2, y_2;
            scanf("%lf%lf%lf%lf", &x_1, &y_1, &x_2, &y_2);
            segs[j ++] = {x_1, y_1, y_2, 1};
            segs[j ++] = {x_2, y_1, y_2, -1};
            tmp.push_back(y_1); tmp.push_back(y_2);
        }
        
        sort(segs, segs + 2 * n);
        sort(tmp.begin(), tmp.end());
        tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end());
        
        build(1, 0, tmp.size() - 2);    
        
        double res = 0;
        for (int i = 0; i < n * 2; i ++) {
            if (i > 0) res += tr[1].len * (segs[i].x - segs[i - 1].x);
            modify(1, find(segs[i].y1), find(segs[i].y2) - 1, segs[i].k);
        }
        
        printf("Test case #%d\n", ++ T);
        printf("Total explored area: %.2lf\n\n", res);
    }
    
    return 0;
}

248. 窗内的星星 - AcWing题库

题解 P1502 【窗口的星星】 - 洛谷专栏 (luogu.com.cn)

思路这篇题解说的很明白，我们来谈谈这个问题为什么需要懒标记。

最重要的一点是，我们线段树中存的数据不再是 \(cnt\) 和 \(len\)，而是 \(sm\) 表示的该子区间对应的亮度总和。亮度的增加不同于 \(cnt\) 是要下传的。并且线段树中叶子存的区间不再是 \([l, l+1]\) 而是 \([l, l]\)，可以理解为一个点。所以我们需要 \(lasytag\) 来帮助操作。

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10010;
int n, w, h;
vector<LL> tmp;

struct Segment {
    LL x, l, r, c;
    bool operator < (const Segment &t) const{
        return x < t.x || x == t.x && c > t.c;
    }
} segs[N * 2];

struct Stree {
    int l, r; 
    LL sm, add; 
} tr[N * 8];

LL find(LL x) {
    return lower_bound(tmp.begin(), tmp.end(), x) - tmp.begin();
}

void pushup(int u) {
    tr[u].sm = max(tr[u << 1].sm, tr[u << 1 | 1].sm);
}

void pushdown(int u) {
    if (tr[u].add) {
        tr[u << 1].sm += tr[u].add;
        tr[u << 1].add += tr[u].add;
        tr[u << 1 | 1].sm += tr[u].add;
        tr[u << 1 | 1].add += tr[u].add;
        tr[u].add = 0; 
    }
}

void build(int u, int l, int r) {
    tr[u] = {l, r, 0, 0};
    if (l != r) {
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
    }
}

void modify(int u, int l, int r, int d) {
    if (l <= tr[u].l && tr[u].r <= r) {
        tr[u].sm += d, tr[u].add += d;
    } else {
        int mid = tr[u].l + tr[u].r >> 1;
        pushdown(u);
        if (l <= mid) modify(u << 1, l, r, d);
        if (r > mid) modify(u << 1 | 1, l, r, d);
        pushup(u);
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);

    while (cin >> n >> w >> h) {
        tmp.clear();
        for (int i = 1, j = 0; i <= n; i ++) {
            LL x, y, c;
            cin >> x >> y >> c;
            segs[j ++] = {x, y, y + h - 1, c};
            segs[j ++] = {x + w - 1, y, y + h - 1, -c};
            tmp.push_back(y); tmp.push_back(y + h - 1);
        }

        sort(tmp.begin(), tmp.end());
        tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end());
        sort(segs, segs + n * 2);  

        build(1, 0, tmp.size() - 1);

        LL res = 0;
        for (int i = 0; i < n * 2; i ++) {
            modify(1, find(segs[i].l), find(segs[i].r), segs[i].c);
            res = max(res, tr[1].sm);
        }

        cout << res << endl;
    }

    return 0;
}

标签：tmp,int,LL,tr,mid,0x40,蓝书,区间
From： https://www.cnblogs.com/biyimouse/p/18607794

相关文章

  • DASCTF 2023 & 0X401七月暑期挑战赛 MyPicDisk
    打开题目是个登录框这里是XXE盲注boogipop师傅的盲注脚本importrequestsimporttimeurl='http://6562827c-cc7e-4a5e-818d-97f9064dfce0.node4.buuoj.cn:81/index.php'strs='abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789'flag=''......
  • DASCTF 2023 & 0X401七月暑期挑战赛【PWN】（VIPhouse篇）
    DASCTF2023&0X401七月暑期挑战赛【PWN】（VIPhouse篇）题目保护情况没有开pie保护，延迟绑定机制64位ida逆向给了一些功能函数1.loginin输入密码的时候会溢出，同时判断输入的name，和passwd同时有两个标志位，如果是admin，多一个标志位2.canary功能前提是admin才能进行输出ca......
  • DASCTF 2023 & 0X401七月暑期挑战赛【PWN】（FileEditor篇）
    DASCTF2023&0X401七月暑期挑战赛【PWN】（FileEditor篇）题目保护情况（保护全家桶）64位ida逆向模拟了一个类似vim的功能，有打开文件，打印内容，插入行，删除行，复制行，和编辑行，还有查找字符和替换字符的功能，然后就是保存退出一个一个来分析吧1.open就是打开一个file文件。没有会创建......
  • 蓝书P364的推论证明
    其实这个证明与前面那个证明很像假设最终生成的生成树不包含这\(m-k\)条边中连接生成森林的两个不连通节点的最小的边，那么我们从这些最小的边中任选一条边加入到树中会形成一个环，而且这个环（除了加入的这条最小边）一定存在一条边不是最开始的\(k\)条边中的某一条（因为如果这个环除了......
  • 板刷蓝书
    最短Hamilton路径状压dp。设\(f_{S,i}\)表示走过的节点状态为\(S\)\((0\)为没走过，\(1\)为走过\()\)，当前在点\(i\)时的最小代价，显然\(S\)的第\(i\)位必须为\(1\)。那么\(f_{S,i}=\min_{S\operatorname{and}2^j=1,j\neqi}\lbracef_{S\operatorname{xor}......
  • DASCTF 2023 & 0X401七月暑期挑战赛-web复现
    别问为什么不复现十一月的那个比赛，因为不会wwwww。EzFlask进去就有源码了，先cv到编辑规范看一下：importuuidfromflaskimportFlask,request,session,jsonfromsecretimportblack_listapp=Flask(__name__)app.secret_key=str(uuid.uuid4())defcheck(data):......
  • 蓝书乱刷
    P2862[USACO06JAN]CorraltheCowsG题意简述给定一个网格\(L\timesL\)，上面有\(N\)个叶子，求最小的正方形边长，使得这个正方形能够覆盖至少\(C\)个叶子题解很显然是一道二分+前缀和的题目，一眼\(O(L^2+N\logL)\)但是题目里\(L\)非常大，带个平方过不去，所以考虑......
  • DASCTF 2023 & 0X401七月暑期挑战赛
    比赛只出了一道，小菜不是罪过-_-controlflow这个题动调到底就行foriinrange(40):after_xor[i]=inp[i]^0x401after_xor[i]+=i*i;foriinrange(11,30,1):x=i-10after_xor[i]^=x*(x+1)foriinrange(40):after_xor[i]-=iafter_xo......
  • DASCTF 2023 & 0X401七月暑期挑战赛——— 解析viphouse
    DASCTF2023&0X401七月暑期挑战赛———解析viphouse保护策略静态分析main  主函数在while循环提供了一个菜单。void__fastcall__noreturnmain(__int64a1,char**a2,char**a3){charnptr[10];//[rsp+Eh][rbp-12h]BYREFunsigned__int64v4;//[rsp......
  • 关于异常DBG_TERMINATE_PROCESS(0x40010004)
    简介DBG_TERMINATE_PROCESS表示进程被调试器终止。值为0x40010004。其定义如下：////MessageId:DBG_TERMINATE_PROCESS////MessageText:////Debuggerterminatedproce......

赞助商

阅读排行

网站主页关于我们联系我们网站地图

本网站内容转载自其他媒体，侵权联系[admin##ips99.com]。

Copyright © 2020-2023 IPS99 版权所有 IPS99